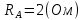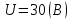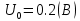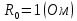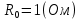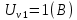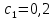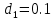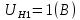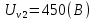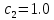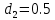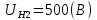КР_Метрология. Задача 10. 3 Задача 7 Задача 10. 8
 Скачать 240.98 Kb. Скачать 240.98 Kb.
|
|
Содержание:
Задача № 1. 10 Задача на оценку предела случайных и систематических погрешностей и погрешности результата прямых измерений
Систематические погрешности: 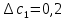 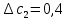 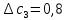 Границы не исключенных остатков: 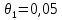 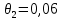 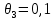 Решение: Среднеарифметическое значение ряда: 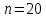 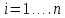
Абсолютная величина отклонения:
Квадрат отклонения
Исправленный ряд наблюдений:
Оценка среднеквадратичных отклонений: среднего арифметического ряда наблюдений:
среднего квадратического отклонения ряда наблюдений:
смещенная оценка среднего квадратического отклонения ряда наблюдений:
Систематическая погрешность:
Граница не исключенных остатков:
Квадрат границы не исключенных остатков:
Наиболее отличающиеся от среднего арифметического систематические погрешности:
Их не исключенные остатки соответственно:
Нормальность распределения результатов наблюдений: Первый критерий: 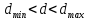 Для уровня значимости 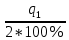
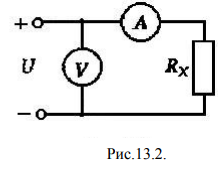
Критерий не выполняется и распределение не нормально Результат измерения 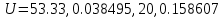 Задача № 3 3адача на оценку предела погрешности косвенных измерений На рис.1 показана схема измерения индукции переменного магнитного поля в магнитопроводе. 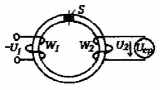 Относительная погрешность частоты: 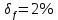 Относительная погрешность площади: 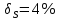 Класс точности вольтметра: 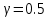 Решение: Относительная погрешность измерения вольтметра: 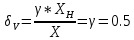 так как стрелка стоит на конечной отметке шкалы: Наибольшая относительная погрешность косвенного измерения функции 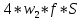 Вид функции:  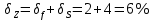 Наибольшая относительная погрешность косвенного измерения индукции: Вид функции: 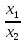 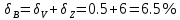 Задача № 10 По показаниям амперметра А и вольтметра V определяется мощность, потребляемая резистором R в цепи постоянного тока. Амперметр класса точности 0.5 со шкалой 0 - 10 А показывает 4 А. Вольтметр имеет шкалу 0 - 200 В, класс точности 1.0 и показывает 150 В. Определите мощность, потребляемую резистором, и максимальную абсолютную погрешность ее измерения.
Решение Активная мощность резистора:
Наибольшая допустимая относительная погрешность измерения: 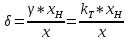 тока
напряжения
Относительная погрешность косвенного измерения мощности: Вид функции 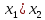
Абсолютная погрешность косвенного измерения мощности:
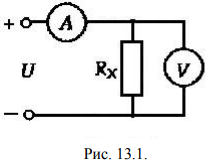
Задача № 12 Ваттметры 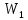 и и 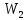 включены на включены на 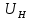 = 150 В и = 150 В и 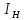 = 5 А. Они имеют класс точности 0.5 и = 5 А. Они имеют класс точности 0.5 и 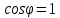 .Ваттметр .Ваттметр 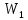 показывает 600 Вт, ( показывает 600 Вт, (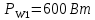 ) ) 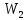 – 400 Вт. ( – 400 Вт. (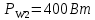 ) Определите реактивную мощность, потребляемую несимметричным приемником, и возможную наибольшую абсолютную погрешность ее измерения. ) Определите реактивную мощность, потребляемую несимметричным приемником, и возможную наибольшую абсолютную погрешность ее измерения.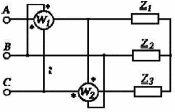 Решение Схема подключения ваттметров, представленная на рисунке, позволяет измерить реактивную мощность трехфазного приемника: 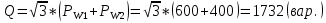 Предел измерения ваттметра: 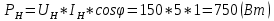 Найдем наибольшую возможную абсолютную погрешность показаний приборов: 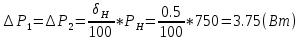 Наибольшая возможная абсолютная погрешность измерения реактивной мощности: 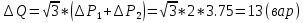 Задача № 15.10 Вывести точные формулы для определения сопротивления RX. Показания к рисунку 13,1 вольтметра и амперметра равны соответственно U и I. Показания приборов и их внутренние сопротивления RV и RA приведены в табл. 7. Определите относительную методическую погрешность измерения сопротивления методом амперметра и вольтметра для каждой схемы. Данные:
Решение Найдем истинное значение сопротивления 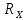 : :
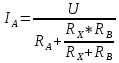 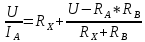 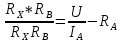 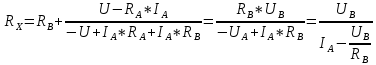 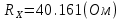 Значение, найденное с помощью амперметра и вольтметра 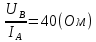 Абсолютная методическая погрешность 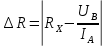 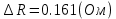 Относительная методическая погрешность
Схема 13,2
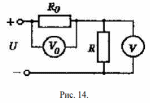
Решение: Найдем истинное значение сопротивления 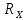 : :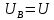 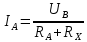 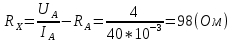 Значение, найденное с помощью амперметра и вольтметра: 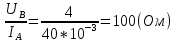 Абсолютная методическая погрешность: 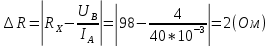 Относительная методическая погрешность: 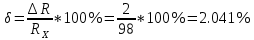 Задача № 17 Системы счисления и коды, применяемые в ЦИП (цифровые измерительные приборы.). Способы преобразования непрерывных величин в коды. Системы счисления, коды: В ЦИУ (цифровые измерительные устройства). кодирование производиться по определённому правилу, например с использованием систем счисления. В привычной для нас десятичной системе счисления любое целое число N может быть представлено в виде: 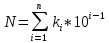 где n – число разрядов. 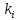 - коэффициент, принимающий значения 0,1,2,3….,9 (используется 10 различных символов). - коэффициент, принимающий значения 0,1,2,3….,9 (используется 10 различных символов).Любое целое число N можно выразить также в двоичной системе: 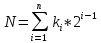 где n – число разрядов. 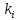 - коэффициент, принимающий значения 0 и 1 (используется 2 символа). - коэффициент, принимающий значения 0 и 1 (используется 2 символа).Наиболее простая система счисления – единичная, имеет один символ (цифра 1), при помощи которого можно выразить любое число, например: Число в десятичной системе счисления: …..1 2 3 4 Число в единичной системе счисления: ……1 11 111 11111…. Для образования кода используют также комбинации целых положительных чисел. Пример: каждый десятичный разряд может быть выражен комбинацией целых положительных чисел a1-an. Эти числа вырубают так, чтобы их линейная комбинация 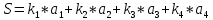 могла принимать любое целое число от 0 до 9 при могла принимать любое целое число от 0 до 9 при 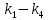 , принимающих значения 0 или 1. Например, , принимающих значения 0 или 1. Например, 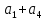 выбирают такими: 2, 4, 2, 1 или 5, 2, 1, 1 и так далее. выбирают такими: 2, 4, 2, 1 или 5, 2, 1, 1 и так далее.При образовании кодов каждому символу используемой системы счисления должен соответствовать свой элемент кода. В зависимости от очередности передачи элементов кода все коды разделяют на последовательные и параллельные. У последовательного кода элементы кода передаются последовательно во времени, причем могут передаваться по одному каналу. У параллельного кода элементы кода одновременно по различным каналам. Если образовывать последовательный код импульсами постоянного тока и считать, что символ двоичной системы счисления соответствует наличие импульса, а отсутствие импульса соответствует символу 0, то число 902 в двоичной системе счисления имеет вид показанный на рисунке 1, а. Каждый импульс кода в зависимости от места (во времени) имеет определённую значимость – “вес”. Код, построенный с использованием двоичной системы, называют двоичным кодом. На рисунке 1, б показан последовательный код в виде импульсов тока, представляющий число 902 в единичной системе счисления. Такой код носит, название число импульсного или единичного кода. Он более громоздок, чем двоичный, однако находит применение в тех случаях, когда измеряемая величина простыми средствами преобразуется в этот код. Достоинство этого кода заключается также в простоте суммирования импульсов кода с помощью пересчетных устройств. Находит применение единичный позиционный код, при использовании которого число выражается положением (порядковым номером) элемента кода на оси времени (последовательный код). На рисунке 1, в, представлен последовательный единичный позиционный код числа 902. При использовании десятичной системы счисления для образования кода требуется десять различных импульсов, например различающихся амплитудой. Такой код не принимают, так как для образования и распознавания этого кода требуется сложная аппаратура, в то время как для образования и переработки двоичного и единичного кодов могут быть использованы простые, так называемые двоичные элементы, имеющие два устойчивых состояния. Поэтому в практике измерений получит применение единично – десятичный код, в котором для передачи значения десятичного разряда требуется десять элементов кода (десять мест расположения импульса) с весами 0, 1, 2,……9 (рисунок 1 г.). 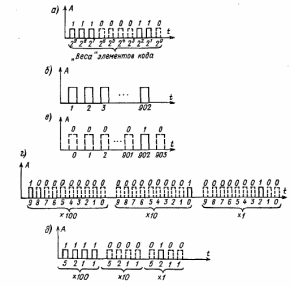 Рисунок 1. Код числа 902: а – двоичный; б – единичный; в – единичный позиционный; г – единично – десятичный; д – при “весах” элементов кода десятичного разряда, равных 5, 2, 1, 1. Двоичный код более компактен (экономичен), чем единично-десятичный. Кроме того, двоичный код вследствие ряда достоинств используют в вычислительных, управляющих и других устройствах. По этой причине двоичный код применяют в АЦП, предназначенных для работы совместно с указанными устройствами. Однако двоичный код неудобен для управления десятичным отсчетным устройством. Поэтому в ЦИП находит применение двоично-десятичный код с «весами» элементов кода одного десятичного разряда, равными 8, 4, 2, 1, а также так называемые тетрадном -десятичные коды с «весами» 2, 4, 2, 1; 4, 2, 2, 1; 5, 2, 1, 1 и т. д. Эти коды более удобны для управления десятичным отсчетным устройством, чем двоичный код, и мало отличаются от двоичного по числу элементов кода. На рис. 1, д показан последовательный код числа 902 при «весах» элементов кода десятичного разряда, равных 5, 2, 1, 1. Согласно требованию стандарта все ЦИП должны выдавать во внешние устройства двоично-десятичный код (8 – 4 – 2 - 1) независимо от кода, применяемого в процессе аналого-цифрового преобразования. Наряду с указанными кодами находят применение так называемые циклические коды, один из которых будет рассмотрен при изучении ЦИУ считывания. Методы преобразования непрерывных измеряемых величин в коды. При аналого-цифровом преобразовании происходит определение отождествляемого уровня квантования, т.е. происходит преобразование непрерывной измеряемой величины в квантованную и образование кода, причем образование кода происходит, как правило, одновременно с преобразованием измеряемой величины в квантованную. По способу преобразования выделяют три основных метода. Метод последовательного счета. При этом методе (рисунок 2, а) происходит последовательное во времени сравнение измеряемой величины х с известной квантованной величиной хк, изменяющейся (возрастающей или убывающей) во времени скачками, причем каждый скачок соответствует шагу (ступени) квантования по уровню. Число ступеней, при котором наступает равенство хk (tH) =x (с некоторой погрешностью), равно номеру отождествляемого уровня квантования. В процессе сравнения образуется единичный код, соответствующий номеру отождествляемого уровня квантования. Возможно инверсное преобразование, при котором известная постоянная величина сравнивается с равномерно квантуемой величиной, функционально связанной с измеряемой величиной. Метод последовательного приближения (сравнения и вычитания, поразрядного уравновешивания). При этом методе (рисунок 2, б) происходит последовательное во времени сравнение измеряемой величины х с известной квантованной величиной хk, изменяющейся во времени скачками по определенному правилу (исключая единичную систему счисления). Значение известной величины, при которой наступает равенство соответствует номеру отождествляемого уровня квантования. Код, образуемый в процессе этой операции, соответствует отождествляемому уровню. Метод считывания. При этом методе (рисунок 2, в) происходит одновременное сравнение измеряемой величины х с известными величинами, значения которых равны уровням квантования. Известная величина, равная измеряемой, дает номер отождествляемого уровня квантования, в соответствии с которым образуется код. 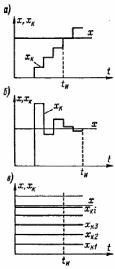 Рисунок 2: Диаграммы преобразований непрерывной измеряемой величины в код Задача № 25,10 Для измерения мощности, выделяемой в нагрузке R (рисунок 14) одним и тем же цифровым вольтметром класса точности с/d, измеряется сначала напряжение на образцовом сопротивлении, выполненном с погрешностью 0,5 %, а потом - на R. У вольтметра имеются пределы по напряжению 0,02-0,2-2-20-200 В. Условный тип вольтметра задан табл. 8: 1 - времяимпульсный; 2 - интегрирующий (двойного интегрирования) - фазового кодирования; 4 – кодоимпульсный; 5 - частотно-импульсный; 6 - комбинированный.
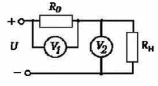
Решение: Ток через образцовое сопротивление: 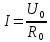 Сопротивление резистора нагрузки: 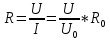 Определим мощность нагрузки: 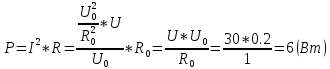 Выберем пределы при измерении напряжения и тока: U=30 B необходим предел 200 В. 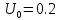 В необходим предел 0,2 В. В необходим предел 0,2 В.Определим относительную погрешность каждой величины: 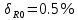 - из данных. - из данных.Погрешности измерения цифровым прибором определим по формуле: 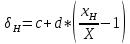 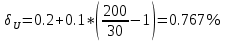 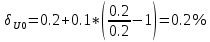 В соответствии с методическими указаниями для функции 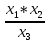 наибольшая возможная относительная погрешность измерения мощности: наибольшая возможная относительная погрешность измерения мощности: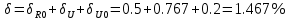 Наибольшая возможная абсолютная погрешность измерения мощности: 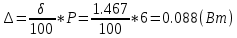 Задача № 30.10 Для измерения мощности, выделяющейся в нагрузке, собрана схема, содержащая два цифровых вольтметра V1,V2 и образцовый резистор R0. Схема показана на рисунке 17. Определите мощность в нагрузке и наибольшую допускаемую погрешность ее измерения (относительную и абсолютную). Сопротивление образцового резистора R0, показания первого вольтметра Uv1, класс точности c1/d1 и предел первого вольтметра взять из таблица 12. а наибольшую допускаемую абсолютную погрешность образцового сопротивления R0, Показания Uv2 второго вольтметра, его класс точности c2/d2 и предел измерений Uн2 приведены в таблице 13.
Решение: Значение тока через образцовое сопротивление: 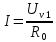 Сопротивление резистора нагрузки: 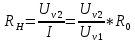 Определим мощность нагрузки: 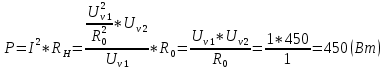 Определим относительную погрешность каждой величины 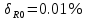 - из данных. - из данных.Погрешности измерения цифровым прибором определим по формуле: 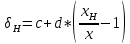 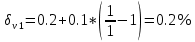 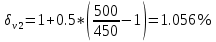 В соответствии с методическими указаниями для функции 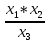 наибольшая возможная относительная погрешность измерения мощности: наибольшая возможная относительная погрешность измерения мощности: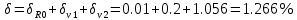 Наибольшая возможная абсолютная погрешность измерения мощности: 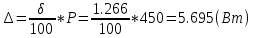 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

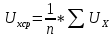
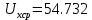
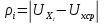
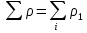
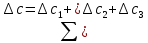
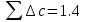
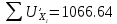
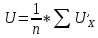
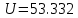
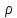
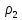
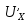
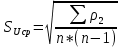
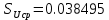
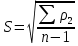
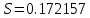
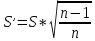
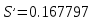
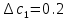
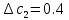
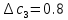
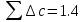
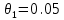
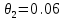
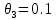
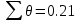
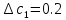
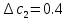
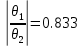
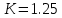
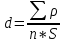
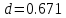 47
47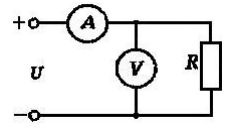
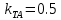
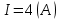
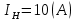
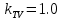
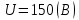
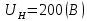
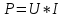
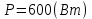
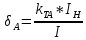
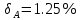
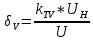
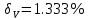
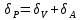
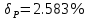
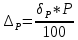
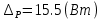
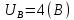
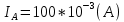
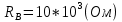
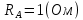
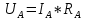
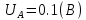
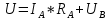
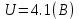
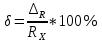
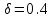
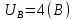
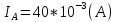
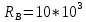 (Ом)
(Ом)