Векторная алгебра. векторная алгебра. Задача 14. Найти площадь треугольника со сторонами если, и Задача 14. Векторы образуют правую или левую тройку
 Скачать 223.5 Kb.
|
|
Контрольная работа 2. Векторная алгебра Задача 1. Даны точки А, В, С. Разложить вектор  по ортам  Найти длину, направляющие косинусы и орт вектора . Найти косинус угла, образованного вектором 
Задача 2. 14. Найти площадь треугольника со сторонами  если  ,  и  Задача 3. 14. Векторы   образуют правую или левую тройку?Образцы решения задач 1. Если известны координаты точек  и  , то координаты вектора  Разложение этого вектора по ортам  :  Длина вектора находится по формуле  а направляющие косинусы:  Орт вектора  Пример. Даны точки  Разложить вектор  по ортам  и найти его длину, направляющие косинусы, орт вектора . Найдем координаторы векторов    и  Вектор       Если  то  .Т  огда 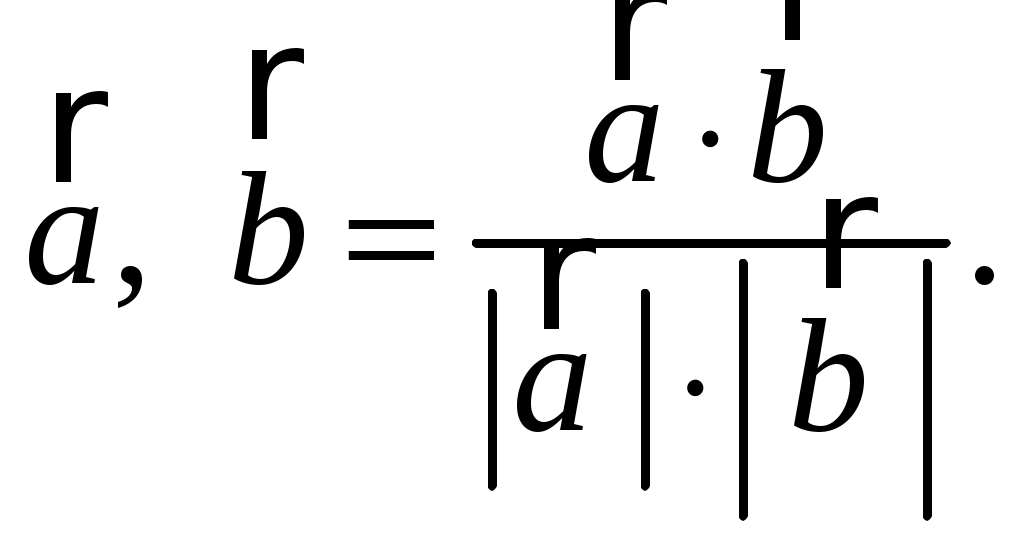  Пример. Даны вершины треугольника  Найти угол при вершине А .  Внутренний угол при вершине А образован векторами     Тогда        2. Даны вершины треугольника  Найти его площадь и длину высоты, опущенной из вершины С. . Находим векторы    Векторное произведение       Так как  где  длина высоты, опущенной из вершины С на сторону АВ,  .   3. Объемы параллелепипеда и тетраэдра (треугольной пирамиды), построенных на векторах  находятся с помощью смешанного произведения векторов: ,  Если  > 0, то тройка векторов  -правая.Если  < 0, то тройка – левая.Если  = 0, то векторы  компланарны.Пример . Дан параллелепипед  , построенный на векторах   и  Найти высоту, проведенную из вершины  на грань ABCD.Объем  равен произведению площади его основания на высоту: находится также по формуле  , поэтому .Вычислим векторное произведение   = 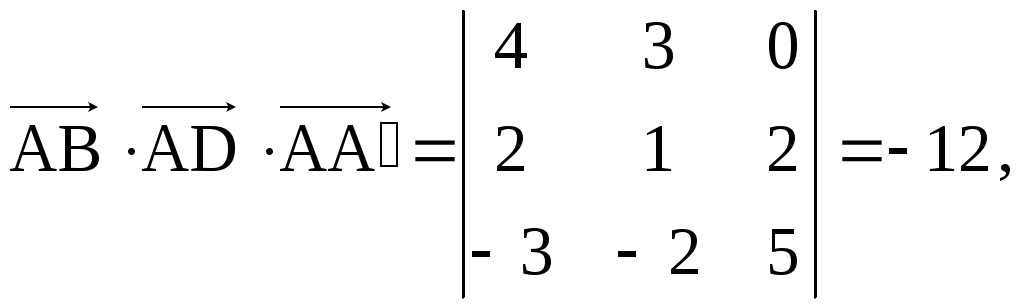    Тогда  ПРИМЕР. Найти объем тетраэдра, построенного на векторах  , Объем тетраэдра в 6 раз меньше объема параллелепипеда, построенного на этих векторах, поэтому 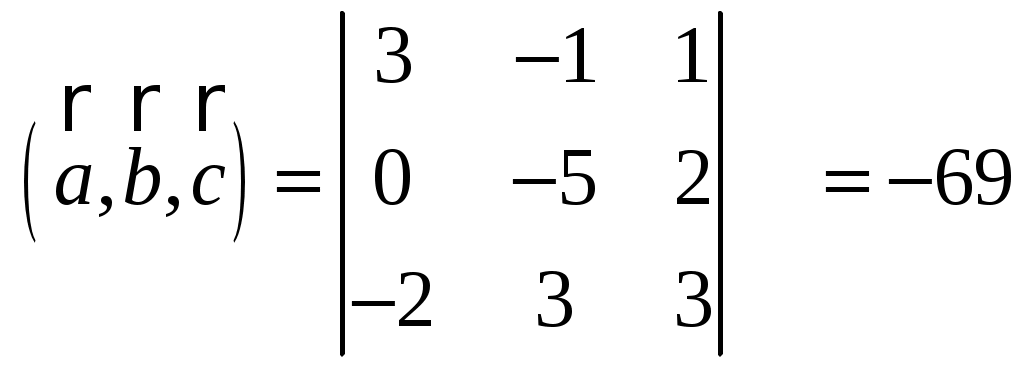   .Отсюда  (заметим, что  – левая тройка, так как смешанное произведение отр |
