Векторная алгебра. ВЕКТОРНАЯ АЛГЕБРА1. Решение. Векторы перпендикулярны, если их скалярное произведение равно нулю. Найдем скалярное произведение векторов и
 Скачать 108.85 Kb. Скачать 108.85 Kb.
|
|
Задание 1 Даны векторы 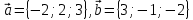 . .1. Проверить перпендикулярность и параллельность векторов. 2. Вычислить 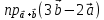 . .3. Найти площадь параллелограмма, построенного на векторах 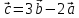 и и 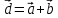 . Сделать рисунок. . Сделать рисунок.Решение. 1. Векторы перпендикулярны, если их скалярное произведение равно нулю. Найдем скалярное произведение векторов 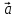 и и 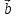 : :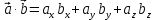 = =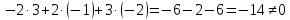 , следовательно, векторы , следовательно, векторы 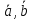 не перпендикулярны. не перпендикулярны.Векторы параллельны, если отношения их координат равны. Найдем отношения координат векторов 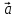 и и 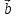 : :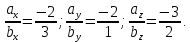 Отношения координат различны, следовательно, векторы 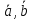 не параллельны. не параллельны.2. Вычислим проекцию вектора 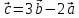 на вектор на вектор 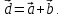 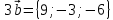 ; ; 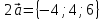 ; ; 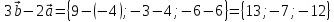 . .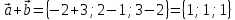 . .Используем формулу: 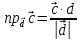 . . Найдем скалярное произведение: 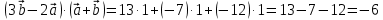 . .Найдем модуль вектора 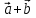 : :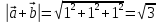 . .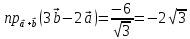 . .3. Площадь параллелограмма, построенного на векторах 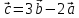 и и 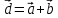 равна модулю векторного произведения этих векторов: равна модулю векторного произведения этих векторов: 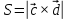 . .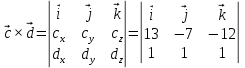 = == 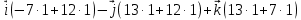 = == 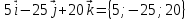 . .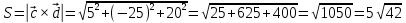 . . ЗАДАНИЕ 2 В прямоугольной системе координат Oxyz даны точки А, В, С, D. Методами векторной алгебры: доказать, что они не лежат в одной плоскости, найти объем пирамиды ABCD, площадь основания АВС, длины боковых ребер, плоские углы при вершине D. Используя полученные данные, найти высоту пирамиды, проведенную из точки D. Решение. A(2; 1; 4), B(-1; 5; -2), C(-7; -3; 2), D(-6; -3; 6). 1) Составим векторы 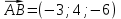 , , 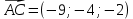 , , 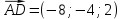 . Если они не компланарны, значит, точки A, B, C, D не лежат в одной плоскости. . Если они не компланарны, значит, точки A, B, C, D не лежат в одной плоскости.Найдем смешанное произведение векторов: 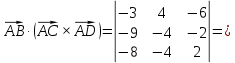 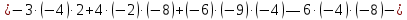 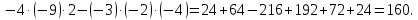 Т.к. смешанное произведение векторов  не равно нулю, значит, они не компланарны и точки А, В, С и D не лежат в одной плоскости. не равно нулю, значит, они не компланарны и точки А, В, С и D не лежат в одной плоскости.2) Найдем объем пирамиды ABCD: 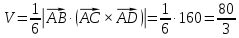 . .3) Найдем площадь основания АВС: 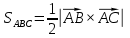 . .Векторное произведение векторов 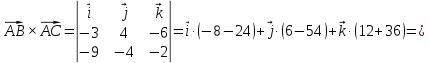 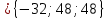 . .Модуль векторного произведения векторов: 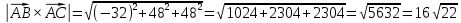 . .Получим: 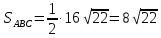 . .4) Найдем длины боковых ребер DA, DB, DC. 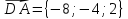 ; ; 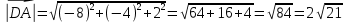 . .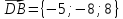 ; ; 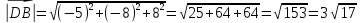 . .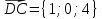 ; ; 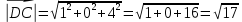 . .5) Найдем плоские углы при вершине D. Угол между векторами 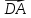 и и 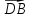 : :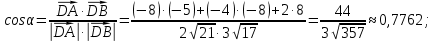 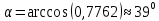 . .Угол между векторами 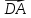 и и 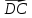 : :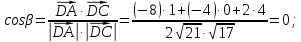 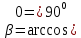 . .Угол между векторами 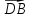 и и 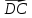 : :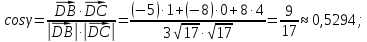 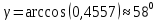 . .6) Найдем высоту пирамиды, проведенную из точки D. 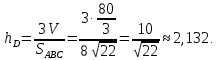 Задание 3. 1. Даны координаты точек А, В, С. Найти: а) уравнение прямой АВ; б) уравнение прямой, которая проходит через точку С перпендикулярно АВ; в) уравнение прямой, которая проходит через точку С параллельно АВ; г) расстояние от точки С до прямой АВ. Уравнения записать в общем виде и с угловым коэффициентом. Прямые показать на чертеже в системе координат xOy. А(-2; 4), В(3; 1), С(10; 7). Решение. а) Каноническое уравнение прямой имеет вид: 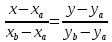 Получим: 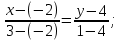 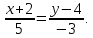 Запишем уравнение прямой в общем виде: 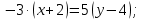 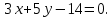 Запишем уравнение прямой АВ с угловым коэффициентом: 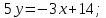 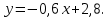 б) Составим уравнение прямой, которая проходит через точку С(10; 7) перпендикулярно АВ. Уравнение прямой, проходящей через точку М(x0,y0) перпендикулярно прямой y=kx+b, имеет вид: 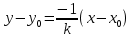 . .Получим: 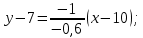 . .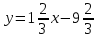 или или 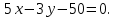 в) Составим уравнение прямой, которая проходит через точку С параллельно АВ. 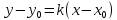 ; ;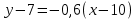 ; ;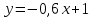 или или 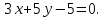 г) Найдем расстояние от точки С(7;10) до прямой АВ с уравнением 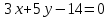 . .Расстояние от точки М(x0, y0) до прямой Ax+By+C=0 определяется по формуле 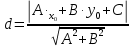 . .Получим: 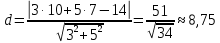 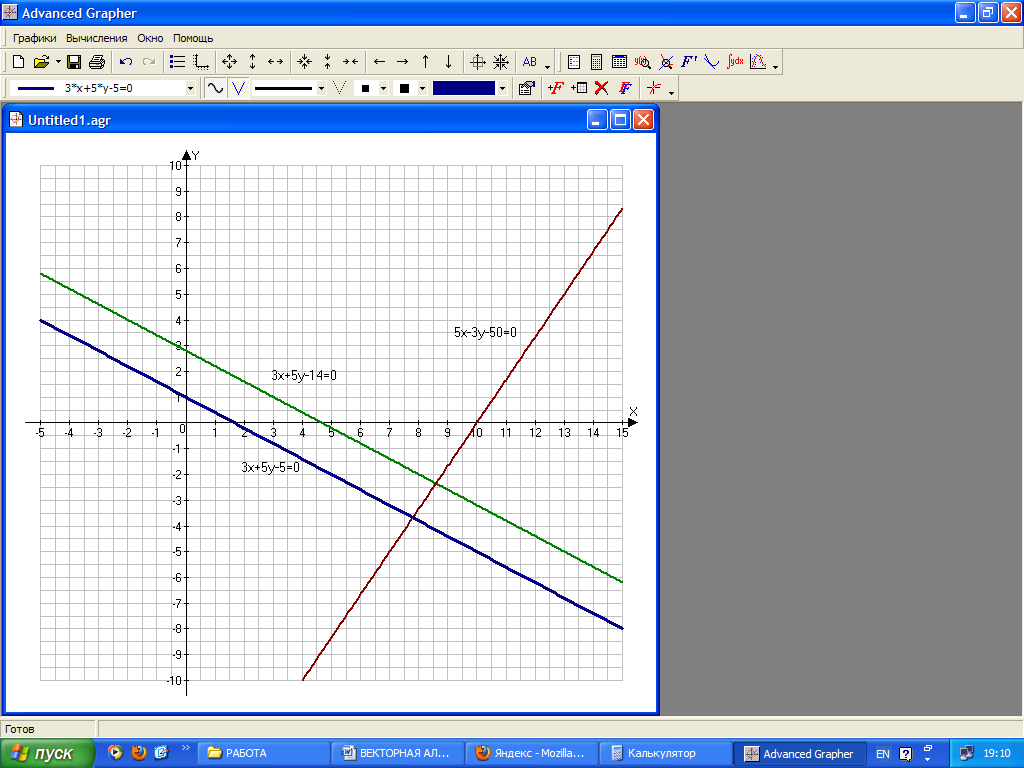 ЗАДАНИЕ 4 Написать каноническое уравнение кривой, применяя метод выделения полного квадрата. Найти координаты центра кривой, координаты вершин. Сделать чертеж в системе координат xOy. 4x2 + 3y2 – 8x + 12y – 32 = 0. Решение. Выделим полные квадраты: 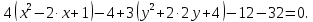 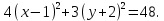 Разделим на 48 обе части: 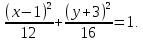 Получили каноническое уравнение эллипса. Найдем параметры кривой. Полуоси эллипса: 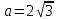 , , 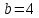 . . Центр эллипса: С(1; -3). Выполним чертеж: 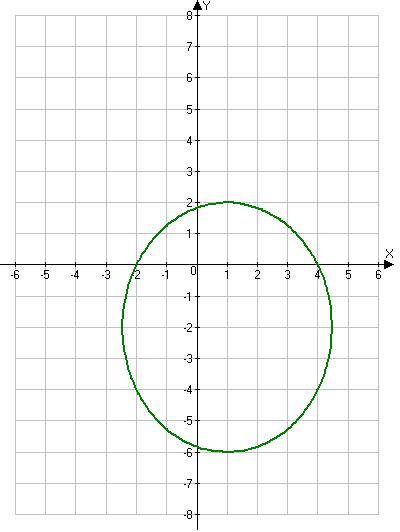 ЗАДАНИЕ 5 Составить уравнение плоскости, проходящей через три точки А, В, С. Сделать условный рисунок. А(-1; 3; 4), В(-1; 5; 0), С(2; 6; 1). Решение. Используем формулу: 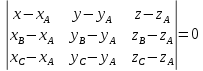 Получим: 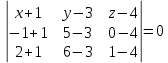 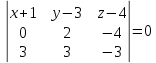 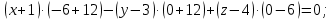 x 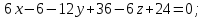 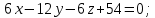 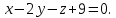  ЗАДАНИЕ 6 Найти точку пересечения прямой и плоскости. Сделать условный рисунок. 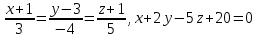 Решение. Представим уравнение плоскости в виде двух уравнений: 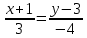 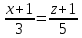 Составим уравнения прямых, лежащих в плоскости: 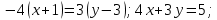 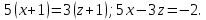 Для нахождения точки пересечения прямой и плоскости решим систему уравнений: 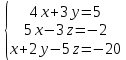 Запишем систему в матричном виде: 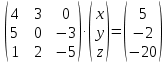 Применим метод Крамера: 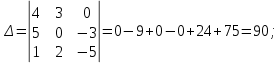 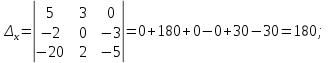 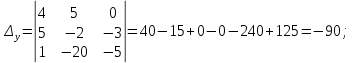 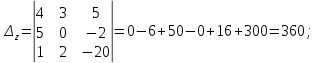 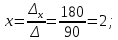 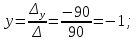 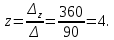 Таким образом, точка пересечения данных прямой и плоскости имеет координаты (2; -1; 4). |
