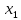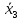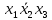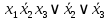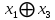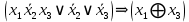Дискретная математика (Задача 6, вариант 4). Задача 6, вариант 4. Задача 2 Даны функции и а вычислить таблицу значений функции
 Скачать 41.27 Kb. Скачать 41.27 Kb.
|
|
Вариант 4 Задача 2 Даны функции  и и  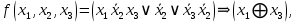 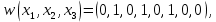 а) вычислить таблицу значений функции 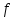 , ,б) найти минимальные ДНФ функций 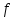 и и 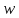 , ,в) выяснить полноту системы 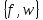 , если система не полна, дополнить систему функцией , если система не полна, дополнить систему функцией 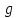 до полной системы, до полной системы,г) из функциональных элементов, реализующих функции полной системы 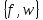 или или 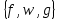 построить функциональные элементы, реализующие базовые функции построить функциональные элементы, реализующие базовые функции 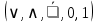 . .Решение: а) вычислим таблицу значений функции 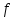 , ,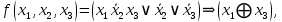
получаем таблицу значений функции 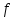
б) найдём минимальные ДНФ функций 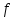 и и 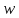 , ,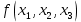 0  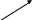 01 0-1 01 0-1 0 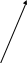  11 -11 11 -11 1  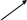 00 1-0 00 1-01  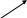 10 11- 10 11-111
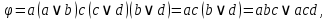 минимальные ДНФ 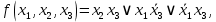 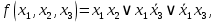
 0  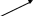  01 0-1 01 0-10 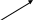 11 -01 11 -01101 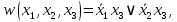 в) выясним полноту системы 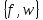 , , на основе теоремы Поста о функциональной полноте, для того, чтобы система булевых функций была полной, необходимо и достаточно, чтобы она включала хотя бы одну функцию, не сохраняющую константы 0, не сохраняющую константы 1, не самодвойственную, нелинейную и немонотонную, одна и та же функция может представлять в функционально полной системе одно или несколько требуемых свойств, 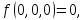 функция функция 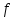 сохраняет 0, сохраняет 0,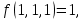 функция функция 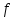 сохраняет 1, сохраняет 1,для противоположных наборов значений аргументов функция не принимает противоположные значения, значит она не самодвойственна, 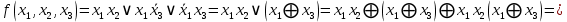 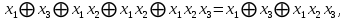 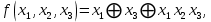 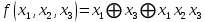 , функция не линейна, , функция не линейна,из таблицы значений видно 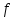 , что функция , что функция 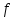 немонотонна, немонотонна, так как 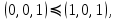 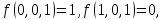 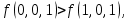  функция функция 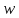 сохраняет 0, сохраняет 0,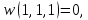 функция функция 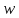 не сохраняет 1, не сохраняет 1,для противоположных наборов значений аргументов функция 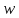 не принимает противоположные значения, значит она не самодвойственна, не принимает противоположные значения, значит она не самодвойственна,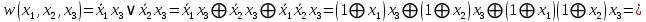 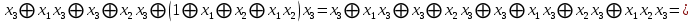 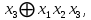 функция не линейна , так как полином Жегалкина этой функции содержит нелинейные члены, из таблицы значений видно, что функция 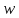 немонотонна, немонотонна, так как 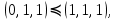 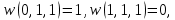 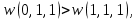 результаты представим в виде таблицы,
система функций 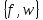 не является полной, так как не содержит функции, которая не сохраняет 0 . не является полной, так как не содержит функции, которая не сохраняет 0 .Дополним систему 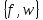 функцией функцией  которая не сохраняет 0 , которая не сохраняет 0 ,
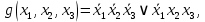 функция 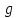 образует с функцией образует с функцией 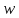 полную подсистему, подобрать функцию полную подсистему, подобрать функцию 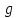 так, чтобы она не образовывала полную подсистему с так, чтобы она не образовывала полную подсистему с 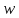 невозможно, так как для функции невозможно, так как для функции 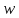 выполняются все условия теоремы Поста о функциональной полноте кроме условия не сохранения 0. выполняются все условия теоремы Поста о функциональной полноте кроме условия не сохранения 0.Представим функции 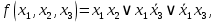 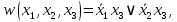 с помощью конъюнкции двух переменных по лемме о нелинейной булевой функции, по лемме о нелинейной булевой функции если булева функция нелинейна, то из неё с помощью подстановки вместо аргументов констант, переменных 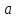 и и 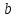 и их инверсий и их инверсий 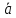 и и 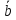 и , возможно, инверсией самой функции, можно получить конъюнкцию 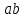 , ,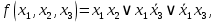 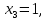 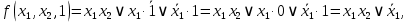 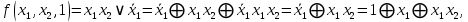 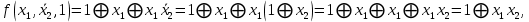 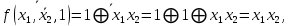 из функции 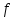 с помощью подстановки вместо аргумента с помощью подстановки вместо аргумента 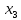 константы 1 , переменной константы 1 , переменной 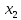 её её инверсии 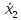 и инверсией самой функции, мы получили конъюнкцию и инверсией самой функции, мы получили конъюнкцию 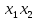 , ,это также доказывает, что функция 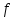 не линейна, не линейна, 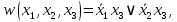 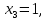 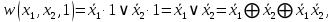 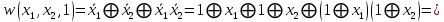 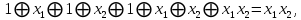 из функции 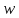 с помощью подстановки вместо аргумента с помощью подстановки вместо аргумента 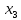 константы 1 мы получили конъюнкцию константы 1 мы получили конъюнкцию 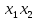 , ,это также доказывает, что функция 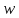 не линейна. не линейна.г) Из функциональных элементов, реализующих функции полной системы 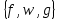 построим функциональные элементы, реализующие базовые функции построим функциональные элементы, реализующие базовые функции 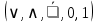 , ,
если все три аргумента 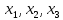 функции функции 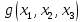 принимают одинаковое значение, то функция принимают одинаковое значение, то функция 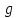 принимает значение, равное их отрицанию, значит отрицание можно представить с помощью функции принимает значение, равное их отрицанию, значит отрицание можно представить с помощью функции 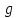 в виде в виде 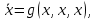 если все три аргумента 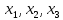 функции функции 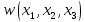 принимают одинаковое значение, то функция принимают одинаковое значение, то функция 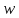 принимает значение, равное 0, значит константу 0 можно представить с помощью функции принимает значение, равное 0, значит константу 0 можно представить с помощью функции 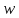 в виде в виде 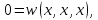 константа 1 – это отрицание константы 0, значит константу 1 можно представить с помощью функций 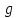 и и 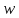 в виде в виде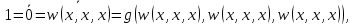 если значение третьего аргумента равно значению первого аргумента функции 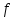 , то функция , то функция 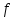 принимает значение, равное значению конъюнкции первого и второго аргументов, значит конъюнкцию можно представить с помощью функции принимает значение, равное значению конъюнкции первого и второго аргументов, значит конъюнкцию можно представить с помощью функции 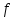 в виде в виде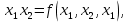 если значение третьего аргумента равно значению второго аргумента функции 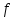 , то функция , то функция 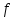 принимает значение, равное значению дизъюнкции первого и второго аргументов, значит дизъюнкцию можно представить с помощью функции принимает значение, равное значению дизъюнкции первого и второго аргументов, значит дизъюнкцию можно представить с помощью функции 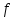 в виде в виде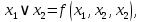 функциональные элементы, реализующие базовые функции 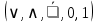 мы построили из функциональных элементов, реализующих функции полной системы мы построили из функциональных элементов, реализующих функции полной системы  в виде в виде 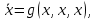 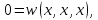 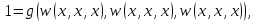 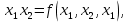 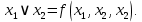 Ответ: 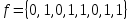 , , минимальные ДНФ 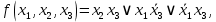 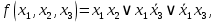 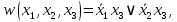 система функций 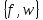 не является полной, не является полной, система дополнена функцией 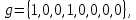 система функций 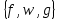 является полной, является полной, 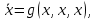 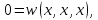 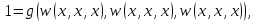 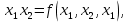 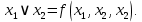 |