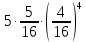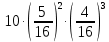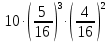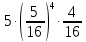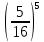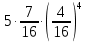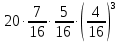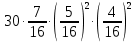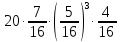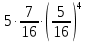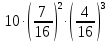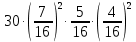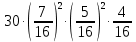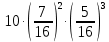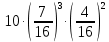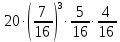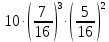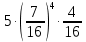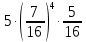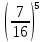Домашняя работа №2 по теории вероятностей.. Задача 2 Условие Проводятся испытания по схеме Бернулли с вероятностью успеха в одном испытании p
 Скачать 30.85 Kb. Скачать 30.85 Kb.
|
|
Задача №2 Условие: Проводятся испытания по схеме Бернулли с вероятностью успеха в одном испытании p. Найти вероятность того, что в n испытаниях число успехов будет не меньше k1 и не больше k2 Найти вероятность того, что в n испытаниях относительная частота успеха будет отличаться от его вероятности не больше чем на E Сколько опытов нужно провести, чтобы с вероятностью 0,95 относительная частота успеха отличалась от его вероятности не больше, чем на E. p=0, 75; n=8000; k1=5950; k2 =6050; E=0, 05. Решение 1) Применяем формулу интегральную теорему Муавра-Лапласа: 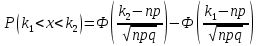 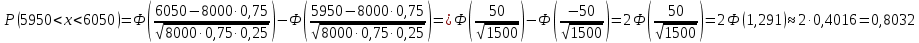 2) Применим формулу 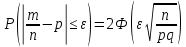 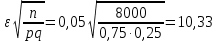 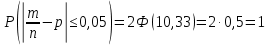 3) Применим формулу 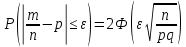 Здесь 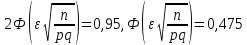 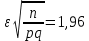 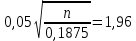 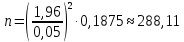 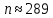 Задача №3 Условие: В урне 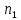 белых шаров, белых шаров, 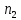 –черных и –черных и 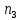 –синих. Наудачу извлекается m шаров. Обозначим через E число вынутых белых шаров, а через µ– черных. Найдите совместное распределение случайных величин E и µ и значение совместной функции распределения FEµ(x,y) в точках (a1, a2), (b1, b2), (c1, c2) и (d1, d2), если выборка производится: А) с возвращением, Б) без возвращения. –синих. Наудачу извлекается m шаров. Обозначим через E число вынутых белых шаров, а через µ– черных. Найдите совместное распределение случайных величин E и µ и значение совместной функции распределения FEµ(x,y) в точках (a1, a2), (b1, b2), (c1, c2) и (d1, d2), если выборка производится: А) с возвращением, Б) без возвращения.В случае Б) найдите законы распределения компонент E и µ, их математические ожидания, дисперсии и коэффициент корреляции. 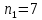 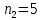 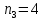 m = 5 (a1, a2)=(6,2) (b1, b2)=(5,3) (c1, c2)=(4,1) (d1, d2)=(2,2) Решение Всего вынимается 5 шаров. Среди них могут быть белые, черные и синие. Рассмотрим все возможные варианты комбинаций шаров
Так как синих шаров всего 4, последнюю комбинацию не рассматриваем. Таким образом, получаем следующие возможные значения пар (E, µ): (0,1), (0,2),(0,3), (0,4) (0,5), (1,0), (1,1), (1,2) (1,3), (1,4), (2,0), (2,1), (2,2), (2,3), (3,0), (3,1), (3,2), (4,0), (4,1), (5,0). В зависимости от типа выборки составим таблицу совместного распределения, учитывая количество возможных вариантов порядка появления шаров Всего шаров 7 + 5 + 4 = 16 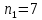 – белых – белых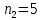 – черных – черных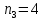 – синих – синиха) выборка с возвращением
F(6,2) = P(E<6,µ<2) = P(1,0)+Р(2,0)+Р(3,0) +Р(4,0) +Р(5,0) +Р(0,1) + P(1,1)+Р(2,1) +Р(3,1) +Р(4,1) = 0,5017 F(5,3) = P(E<5,µ<3) = P(1,0)+Р(2,0)+Р(3,0) +Р(4,0) +Р(0,1) + P(1,1)+Р(2,1) +Р(3,1) +Р(4,1)+ Р(0,2) + P(1,2)+Р(2,2) +Р(3,2) +Р(4,2) = 0,8030 F (4,1) = P(E<4,µ<1) = P(1,0)+Р(2,0)+Р(3,0) = 0,0908 F(2,2) = P(E<2,µ<2) = P(1,0)+Р(0,1)+Р(1,1) = 0,0574 б) выборка с возвращением 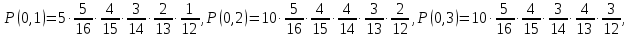 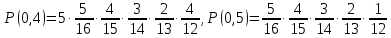 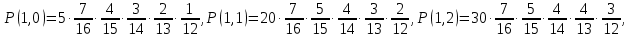 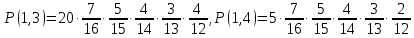 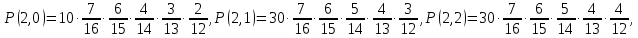 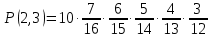 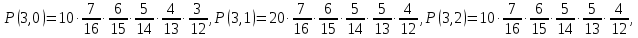 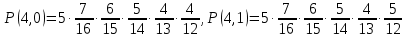 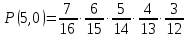
F(6,2) = P(E<6,µ<2) = P(1,0)+Р(2,0)+Р(3,0) +Р(4,0) +Р(5,0) +Р(0,1) + P(1,1)+Р(2,1) +Р(3,1) +Р(4,1) = 0,4836 F(5,3) = P(E<5,µ<3) = P(1,0)+Р(2,0)+Р(3,0) +Р(4,0) +Р(0,1) + P(1,1)+Р(2,1) +Р(3,1) +Р(4,1)+ Р(0,2) + P(1,2)+Р(2,2) +Р(3,2) +Р(4,2) = 0,8565 F (4,1) = P(E<4,µ<1) = P(1,0)+Р(2,0)+Р(3,0) = 0,0689 F(2,2) = P(E<2,µ<2) = P(1,0)+Р(0,1)+Р(1,1) = 0,0348 Законы распределения компонент E и µ, их математические ожидания, дисперсии и коэффициент корреляции
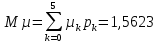 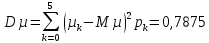
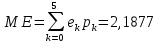 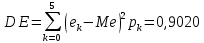 Коэффициент корреляции 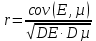 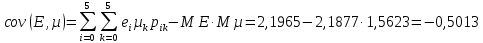 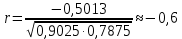 Задача №4. Случайная величина 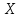 имеет распределение Лапласа с плотностью имеет распределение Лапласа с плотностью 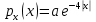 . Определите коэффициент . Определите коэффициент 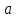 , функцию распределения , функцию распределения 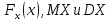 . .Решение. Найдем 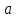 из условия нормировки плотности: из условия нормировки плотности: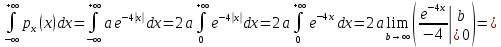 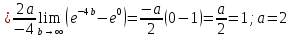 Найдем функцию распределения 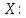 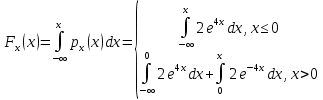 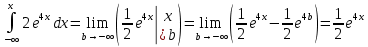 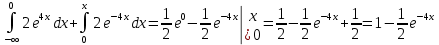 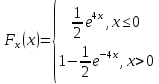 Найдем математическое ожидание и дисперсию. 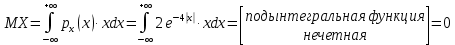 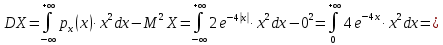 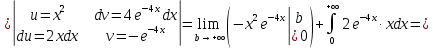 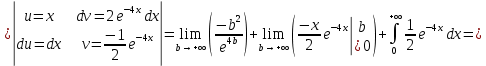 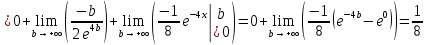 Ответ.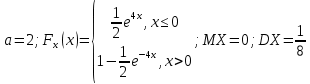 |