Задача 2 Вариант 2. 3

• Название: Задача 2 Вариант 2. 3
• Дата: 08.01.2023
• Размер: 302.34 Kb.
• Имя файла: _9757739.docx
• Тип: Задача; #876269
• страница: 1 из 3

Задача №2 Вариант №2.3

С завода поступило n партий измерительных приборов, по 20 приборов в каждой партии, из которых k приборов имеют знак качества. Наудачу отбираются по одному прибору из каждой партии.

1. 
   Построить ряд и функцию распределения числа приборов со знаком качества среди отобранных, если n=4 и k=3. Вычислить математическое ожидание и дисперсию рассматриваемой случайной величины.
   
2. 
   Оценить вероятность того, что среди отобранных будет хотя бы один прибор со знаком качества, если n=40 и k=1.
   

Решение

1. 
   Вероятность того, что из каждой партии взят прибор со знаком качества равна:
   

р = ³

20

Вероятность того, что из каждой партии взят прибор без знака качества равна: _q= 17



20


п
Обозначим сл. вел. Х – число приборов со знаком качества среди отобранных Х имеет биномиальное распределение. Каждая вероятность считается по

формуле Бернулли Р_п(т)=

n=4 p=0,15

q=1-p=0,85

С^т р^т q^п-т.

4
р(Х=0)=р₄(0)=С⁰ ∙ 0,15⁰ ∙ 0,85⁴ = 0,522


4
р(Х=1)=р₄(1)=С¹ ∙ 0,15¹ ∙ 0,85³ = 0,368


4
р(Х=2)=р₄(2)=С² ∙ 0,15² ∙ 0,85² = 0,098


4
р(Х=3)=р₄(3)=С³ ∙ 0,15³ ∙ 0,85¹ = 0,011


4
р(Х=4)=р₄(4)=С⁴ ∙ 0,15⁴ ∙ 0,85⁰ = 0,001

Ряд распределения:

Х	0	1	2	3	4
Р	0,522	0,368	0,098	0,011	0,001

Вычислим математическое ожидание M(X)=1*0.368+2*0.098+3*0.011+4*0.001=0,6

Вычислим дисперсию

D(X)  M(X² )  M² (X) 

= (1² ∗ 0.368 + 2² ∗ 0.098 + 3² ∗ 0.011 + 4² ∗ 0.001) − 0,6² ≈ 0,51

Запишем функцию распределения:

𝐹⁽𝑋⁾ =

0, 𝑥 ≤ 0,





0,522, 0 < 𝑥 ≤ 1

0,89, 1 < 𝑥 ≤ 2

0,988, 2 < 𝑥 ≤ 3

^{0,999, 3 < 𝑥 ≤ 4}

^{ 1, 𝑥 > 4

Построим график функции распределения: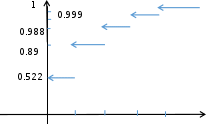
F(x)


x

^{0 1} _{2 3} 4


2)

Вероятность того, что из каждой партии взят прибор со знаком качества равна:

р = ¹

20

Вероятность того, что из каждой партии взят прибор без знака качества равна: _q= 19



20


п
Обозначим сл. вел. Х – число приборов со знаком качества среди отобранных Х имеет биномиальное распределение. Каждая вероятность считается по

формуле Бернулли Р_п(т)=

n=40

p=1/20

q=1-p=19/20

С^т р^т q^п-т.

р(Х=0)= р

(0)=⁰

1 ⁰

₁₉ 40

нет приборов со знаком качества.

40

40
С ∙ ( )

20

• 
  ( )
  

20

≈ 0,129 −

Вероятность того, что среди отобранных будет хотя бы один прибор со знаком качества р=1-0,129=0,871
Задача №3 Вариант №3.3

Непрерывная СВ Х задана функцией распределения F(x). Найти: а) значения коэффициентов А и В,

б) плотность распределения f(x),

в) вероятность того, что СВ Х примет значение в интервале (x = ^𝜋 , х

= ^𝜋),

г) математическое ожидание и дисперсию СВ Х,

1 ₃ 2 ₂

д) построить графики F(x) и f(x).
0 при 𝑥 ≤ 0,

𝐹⁽𝑥⁾ = {А⁽В − 𝑐𝑜𝑠𝑥⁾ при 0 ≤ 𝑥 ≤ 𝜋 ,

1 при 𝑥 ≥ 𝜋
Решение а)

𝐹⁽0⁾ = А⁽В − 𝑐𝑜𝑠0⁾ = А⁽В − 1⁾ = 0
𝐹⁽𝜋⁾ = А⁽В − 𝑐𝑜𝑠𝜋⁾ = А⁽В + 1⁾ = 1

Решаем систему уравнений
Откуда
А⁽В − 1⁾ = 0

А⁽В + 1⁾ = 1
В = 1, А = 0,5

0 при 𝑥 ≤ 0,

𝐹⁽𝑥⁾ = {0.5⁽1 − 𝑐𝑜𝑠𝑥⁾ при 0 ≤ 𝑥 ≤ 𝜋

1 при 𝑥 ≥ 𝜋
б) плотность распределения f(x)
0 при 𝑥 ≤ 0,

𝑓⁽𝑥⁾ = 𝐹′⁽𝑥⁾ = {^{0.5 ∙ 𝑠𝑖𝑛𝑥 при 0 ≤ 𝑥 ≤ 𝜋}

0 при 𝑥 ≥ 𝜋

в) вероятность того, что СВ Х примет значение в интервале (x
= ^𝜋 , х
= ^𝜋),

1 ₃ 2 ₂

𝜋 𝜋 𝜋 𝜋 𝜋 𝜋

𝑃 (

3

≤ 𝑋 ≤

) = 𝐹 ( 2 3

) − 𝐹 (

₂) = 0.5(1 − 𝑐𝑜𝑠

₂) − 0.5 (1 − 𝑐𝑜𝑠

₃) =

= 0.5⁽1 − 0⁾ − 0.5⁽1 − 0.5⁾ = 0.5 + 0.25 = 0.75
г)
найдем математическое ожидание M(x)

+∞ 𝜋

𝜋 𝜋

М⁽Х⁾ = ∫ 𝑥 ∙ 𝑓⁽𝑥⁾𝑑𝑥 = ∫ 0.5𝑥𝑠𝑖𝑛𝑥𝑑𝑥 = 0.5⁽𝑠𝑖𝑛𝑥 − 𝑥𝑐𝑜𝑠𝑥⁾ | =



−∞ 0 ^{0 2}

найдем дисперсию D(x)

+∞ 𝜋

2 2 2

_𝜋 2

𝐷⁽Х⁾ = ∫ 𝑥 ∙ 𝑓⁽𝑥⁾𝑑𝑥 − 𝑀 ⁽𝑥⁾ = ∫ 0.5𝑥

−∞ 0

𝑠𝑖𝑛𝑥𝑑𝑥 − ( ) =

2

_{( 2 )} 𝜋 𝜋 ²

= 0.5

2𝑥𝑠𝑖𝑛𝑥 − (2 − 𝑥

)𝑐𝑜𝑠𝑥

| − ( )

0 2

≈ 1,364

д) построим график F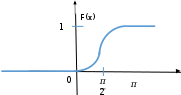(x)

x


график функции распределения f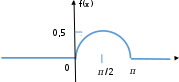(x)

x

Задача №4 Вариант 4.3

СВ Х задана плотностью распределения. Найти:

а) значение коэффициента А,

б) функцию распределения F(x),

в) вероятность того, что СВ Х примет значение в интервале (х₁, х₂),

г) вероятность того, что СВ Х в n независимых испытаниях, проводимых в одинаковых условиях, ни разу не попадает в интервал (х₁, х₂),

д) математическое ожидание и среднеквадратичное отклонение СВ Х, е) построить графики F(x) и f(x). х1=1, х2=3, n=4

_{𝑓(𝑥) = {}𝐴𝑥² + 𝑏𝑥 + 6 при 2 ≤ 𝑥 ≤ 4,

0 при х > 2 или х < 4

Решение

а)

4 4

2
𝑥³ 𝑏 ₂ 4

∫ f⁽x⁾dx = ∫ ⁽𝐴𝑥 + 2𝑥 + 6⁾𝑑𝑥 = (𝐴 ₃ + ₂ 𝑥 + 6𝑥) | =