Вариант 26- Задача1-4. Задача 2 Вариант 26 к р. 2 Рассчитать сложную схему. Проверить баланс мощностей а I 6 i 1
 Скачать 224.86 Kb.
|
|
Вариант 26 Найти все токи, напряжения, ЭДС. Проверить баланс мощностей.   I2 I4 d R1 = 5 Ом  R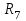 2 = 9 Ом I1 I3 R3 = 10 Ом b R4 = 8 Ом R5 = 4 ОмR6 = 6 Ом I6 I7 R7 = 10 Ом   R8 = 12 Ом  I5 R0 = 14 Ом I7 = 4 A I8 а 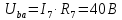 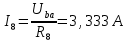 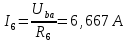 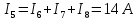 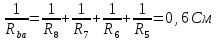 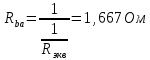 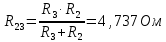 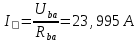 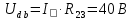 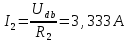 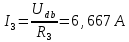 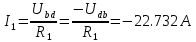 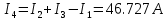 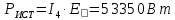 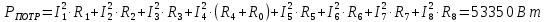 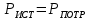  Задача 2 Вариант 26* к.р.2 Рассчитать сложную схему. Проверить баланс мощностей.   а I6   I1 R1 = 10 Ом I4 R2 = 5 Ом R3 = 10 Ом  b d R4 = 10 Ом I3 R5 = 5 Ом I5 I2 R6 = 8 Ом c E = 10 В  R7= R1R2/( R1+R2 + R6) 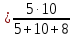 = 2,174 ОмR8= R2R6/( R1+R2 + R6)= 1,739 Ом R9= R1R6/( R1+R2 + R6)= 3,478 Ом   а R9 R8 R7 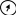 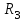 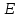 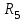 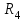 I4 b о d  I3 I5  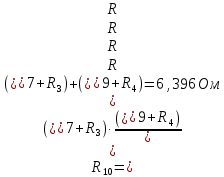 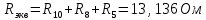 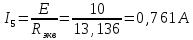 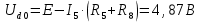 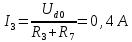 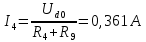 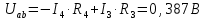 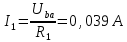 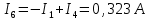 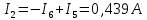 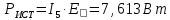 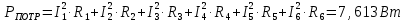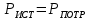а Вариант 26 кр3  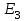 r1 = 3 Ом I4 r2 = 6 Ом I5 I6 r3 = 9 Ом  r4 = 7 Ом r5 = 4 Ом r6 = 2 Ом E1 = 6 В d c b E2 = 10 В  I3 I1 E3 = 8 В  I2 Рассчитать токи методом законов Кирхгофа, предварительно упростив схему, и проверить баланс мощностей. Разложим заданную электрическую цепь не её геометрические элементы: ветви – n = 6, узлы m = 4, независимые контуры – p=3. Произвольно зададимся условно положительными направлениями тока в ветвях, число составляемых уравнений в системе равно числу неизвестных токов, т. е. 6 (I1, I2, I3, I4, I5, I6). Для произвольных узлов составим уравнения на основании 1 закона Кирхгофа. Число их для рассматриваемой схемы m-1=4-1=3 I4 – I5 – I6 = 0 – для узла а; I5 – I1 + I2 = 0 – для узла b; I1 – I4 – I3 = 0 – для узла с; На основании II закона Кирхгофа составим недостающее в системе число уравнений n-(m-1)=6-(4-1)=3, т.е. количество уравнений, равное числу независимых контуров. Произвольно выберем направление обхода контуров (Н.О. – обозначим стрелкой). -I1R1 – I5R5 – I4 R4= -E1 - E2 - для контура acba (I) I6R6 – I3R3+ I4 R4 = -E3 + E1 - для контура cadc (II) I1R1 + I3R3 + I2 R2= E2+ E3для контура bcdb (III)  I4 – I5 – I6 = 0;I5 – I1 + I2 = 0 I1 – I4 – I3 = 0 -I1R1 – I5R5 – I4 R4= -E1 - E2 I6R6 – I3R3+ I4 R4 = -E3 + E1 I1R1 + I3R3 + I2 R2= E2+ E3 Подставим заданные числовые значения Э.Д.С. и сопротивлений и решим ее относительно неизвестных токов методом Крамера         A A     A A     A A Вт Вт Вариант 26 к.р.4 R  1 = 2 ОмR2 = 8 Ом  R3 = 5 Ом R4 = 4 Ом   I6 I2 R5 = 6 Ом I5 I4 I1 R6 = 5 Ом   E1 = 5 В E2 = 4 В E3 = 6 В I3 Независимые контуры – p=3.  I4 Произвольно зададимся условно положительными направлениями контурных токов в независимых контурах (I11, I22, I33) и условно положительным направлением их обхода (Н.О.).  На основании II закона Кирхгофа, для контурных токов, составим систему уравнений I11 (R1+R6+ R4) – I22 R6 – I33R4 = – E1 для контура (I) I22 (R2+ R5+ R6) – I11 R6 – I33R5 = E2 - для контура (II) I33(R4+ R3+ R5)– I22R5 – I11 R4= E3 для контура (III) Подставим заданные числовые значения Э.Д.С. и сопротивлений и решим ее относительно неизвестных контурных токов.  I11 (2+5+4) – I22 5– I334 = -5I22 (8+6+5) – I11 5 – I336 = 4 I33(5+ 6+ 4)– I22 6 – I11 4= 6              I11 = -0.117 I22 = 0.339 I33 = 0.504 Значения искомых токов в ветвях определяются по найденным числовым значениям контурных токов I1= -I11=0.117A; I2= I22=0.339A; I3= I33= 0.504 A; I4= I33-I11= 0.621A; I5= I22- I33= -0.165; I6= I22- I11= 0.456A.  Вт Вт |