фин анализ. Задача 2 Задание Тест 2 Задание Расчетные задачи 2 Задание Ситуационная задача
 Скачать 79.5 Kb.
|
|
ВАРИАНТ № 17 ОглавлениеЗадание 1. Ситуационная задача 2 Задание 2. Тест 2 Задание 3. Расчетные задачи 2 Задание 1. Ситуационная задачаИмущество организации стоимостью 18 млн. руб. было застраховано на один год у двух страховщиков: у страховщика № 1 – на страховую сумму 16,0 млн. руб., у страховщика № 2 – на 5,7 млн. руб. (двойное страхование). В результате страхового случая, предусмотренного договором страхования, имущество погибло. Определите, в каком размере каждый страховщик выплатит страховое возмещение страхователю. Решение Страховое возмещение страховщика 1: СВ1= 16/ (16+5,7)*18=13,27 Страховое возмещение страховщика 2: СВ1= 5,7/ (16+5,7)*18=4,72 Ответ: 13, 27 и 4, 27 Задание 2. Тест1. Отзыв лицензии на проведение страховой деятельности влечет за собой: а) прекращение права юридического лица осуществлять страховую деятельность; б) исключение юридического лица из Единого Государственного реестра страховщиков и объединений страховщиков; в) оба ответа верны. 2. Двойное страхование – это: а) ответственность страховщика по двум и более страховым событиям, включенным в договор страхования; б) страхование одного объекта в страховой сумме, превышающей действительную стоимость объекта; в) страхование объекта у двух или нескольких страховщиков в страховой сумме, превышающей страховую стоимость объекта. Задание 3. Расчетные задачи1. Определите единовременный брутто-взнос при страховании мужчины на случай смерти на четыре года, если возраст застрахованного x = 36 лет, годовая норма доходности i = 8%, страховая сумма S = 500 000 руб., нагрузка в структуре тарифной ставки f = 11%. Решение Для решения задачи необходимо составить уравнение эквивалентности, то есть приравнять обязательства страхователя и страховщика на момент заключения договора. Для этого приведем (дисконтируем) взносы страхователей и ожидаемые выплаты страховой компании на момент начала договора страхования. Для простоты решения будем полагать, что страховщик производит страховые выплаты в конце года, в котором наступила смерть застрахованного лица.  Будем рассуждать следующим образом: все живущие мужчины в возрасте 47 лет (из таблицы смертности их число равно ) заплатят взнос в размере . Образуется страховой фонд в размере . Этой суммы денег должно хватить на все выплаты страховщика. Рассчитаем ожидаемую стоимость страховых выплат страховщика. В течение первого года страхования число умерших (из таблицы смертности) равно . По каждому случаю смерти страховщик выплачивает страховую сумму . Поэтому в конце первого года страховщик должен выплатить общую сумму . Дисконтируем эту сумму на начало (на момент заключения) договора: . В течение второго года страхования число умерших равно (число умерших в возрасте 48 года). Поэтому в конце второго года страховщик должен выплатить сумму . Дисконтируем эту сумму на начало договора, то есть на два года назад: .   В течение третьего года страхования число умерших равно . Поэтому в конце третьего года страховщик должен выплатить сумму . Дисконтируем эту сумму на начало договора: . Составляем уравнение эквивалентности:  (1) Тарифной ставкой называется ставка взноса с единицы страховой суммы. Поэтому из уравнения (9) найдем нетто-ставку Tn как отношение взноса P к страховой сумме S. Для этого разделим правую и левую часть уравнения сначала на S:  (2) а затем полученное уравнение разделим на : 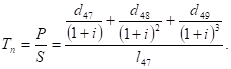 (3) Подставив данные из условия задачи из таблицы смертности , получим: 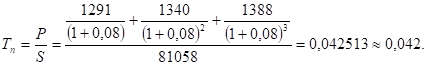 Вычислим брутто-ставку:  Рассчитаем страховую премию при страховой сумме 35000 руб.:  (4)  Следовательно, страхователь заплатит 1634,5 рублей в качестве страхового взноса. В случае смерти застрахованного страховая компания выплатит 35000 рублей выгодоприобретателю, указанному в страховом полисе. Ответ: брутто-ставка равна 4,67%; страховая премия равна 1634,5 рублей. Страховая сумма 2. Вычислите брутто-взнос при страховании от несчастного случая, если вероятность наступления страхового событияp = 0,13, отношение средней выплаты к средней страховой сумме  , нагрузка в структуре тарифной ставки f = 33%, планируемое количество договоров N = 20 000, вероятность неразорения компании γ = 0,95, страховая сумма по договору страхования равна S = 160 000 руб.Решение Нетто-ставка для видов страхования иных, чем страхование жизни, рассчитывается по формуле:  где - основная часть нетто-ставки, (2)  - рисковая надбавка. (3) Здесь N - планируемое количество договоров страхования, б(г) - квантиль, который берется из таблицы 1 в соответствии с вероятностью не разорения компании г. Таблица 1- Значения квантилей нормального распределения.
Вычислим основную часть тарифной ставки:  Вычислим рисковую часть тарифной ставки:  (4)  Затем вычислим нетто-ставку: (5) Вычислим брутто-ставку:  (6)  Ответ: тарифная ставка при страховании имущества предприятий равна 0,65%. |