МОДЕЛЬ ПОТРЕБИТЕЛЬСКОГО ВЫБОРА. статья. Модель потребительского выбора
 Скачать 72.69 Kb. Скачать 72.69 Kb.
|
|
I (1) МОДЕЛЬ ПОТРЕБИТЕЛЬСКОГО ВЫБОРА Будем полагать, что имеется n различных товаров. Тогда некоторый набор товаров будем обозначать через n - мерный вектор x = (x1, x2, ….., xn) где хi - количествоi-го товара. Естественные ограничения на набор товаров – это хi  0 (i= 1,2,...,п); в условной записи х 0 (i= 1,2,...,п); в условной записи х  0, где 0 - нулевой вектор. Множество всех наборов товаров X называется пространством, так как в нем можно сложить любые два набора и умножить любой набор на любое неотрицательное число (последнее справедливо для случая безграничной делимости и умножения товаров). 0, где 0 - нулевой вектор. Множество всех наборов товаров X называется пространством, так как в нем можно сложить любые два набора и умножить любой набор на любое неотрицательное число (последнее справедливо для случая безграничной делимости и умножения товаров).Выбор индивида-потребителя характеризуется отношением предпочтения: считается, что потребитель может сказать о любых двух наборах, какой более желателен, или он не видит между ними разницы. Отношение предпочтения транзитивно: если набор х предпочтительнее наборау, а наборупредпочтительнее набораz, то набор х предпочтительнее набораz. Будем полагать, что поведение потребителя полностью описывается аксиомой индивида - потребителя: каждый индивид-потребитель принимает решения о потреблении, покупках и т.п.,исходя только из своей системы предпочтений. Функция полезности На множестве потребительских наборов X определена функция (2) и(х) = u(x1, x2,…. xn), значение которой на потребительском наборе x равно потребительской оценке индивида для этого набора. Функцияи(х) называетсяфункцией полезности потребителя или функцией потребительского предпочтения. Согласно этому определению каждый потребитель имеет свою функцию полезности. Однако все множество потребителей можно разделить на определенные классы потребителей (по возрасту, имущественному положению и т.п.) и каждому классу приписать некоторую, может быть, осредненную функцию полезности. Таким образом, функцияи(х) является потребительской оценкой или уровнем удовлетворения потребностей индивида при приобретении данного набора х. Если набор x предпочтительнее набора y для данного индивида, то и(х)>u(y). (3) Укажем свойства функции полезности в предположении о ее дифференцируемости. 1.  δu/δxi = и’i >0, i = 1,2,3, ..., п. δu/δxi = и’i >0, i = 1,2,3, ..., п.Первые частные производные функции полезности называютсяпредельными полезностями продуктов. Из этого свойства вытекает, что если x’k > х”k при неизменных количествах других продуктов, то u(x1,.., х’k, хк+1,..., хn) > u(х1,..., х”k, xk+1,….xn), т.е. возрастание потребления одного продукта при неизменном потреблении других продуктов приводит к росту потребительской оценки. Заметим, что векторδи/δх = (δu/δx1, δи/δх2,…., δu/δxn ) является градиентом функции и(х); он показывает направление наибольшего роста функции. Для функции полезностии(х) ее градиент представляет собой вектор предельных полезностей продуктов. (4) 2. δ2u/δ2xi = и”I <0, i = 1,2,3,…., п. т.е. предельная полезность любого товара уменьшается с ростом его потребления. Это утверждение называетсязаконом Госсена (немецкий экономист XIX века, впервые на практике установивший эту закономерность). 3. δ2u/(δxiδxj) = и”ij >0, i≠j (i,j= 1,2,3, ...,n). (5) Это свойство означает, что предельная полезность каждого продукта увеличивается с ростом количества другого продукта. Нетрудно видеть, что указанные свойства функции полезности аналогичны свойствам 3-5 производственной функции. Формально это следует из трактования функции полезности как производственной функции, ресурсами которой являются товары, а выпуском - уровень удовлетворения потребностей индивида. Приведем несколько видов функций полезности, удовлетворяющих принятым допущениям. Неоклассическая: и(х1, х2)= хα1хβ2, α, β > 0, α+β < 1. (6) Квадратическая: и(х) = 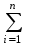 aixi + aixi + 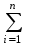 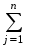 bijxixj (7) bijxixj (7)где матрица ||bij || отрицательно определена и аi + 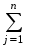 bij >0 для i = 1,2,3 .. ., n. bij >0 для i = 1,2,3 .. ., n. 3. Логарифмическая функция: и(х) = 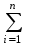 ai logd (xi – bi ), (8) ai logd (xi – bi ), (8)гдеai >0, xi > bi ≥ 0 дляi = 1,2,3 .. .,n. Линии безразличия В прикладных задачах и моделях потребительского выбора часто используется частный случай набора из двух товаров, т.е. когда функция полезности зависит от двух переменных. Здесь вводится понятиелинии безразличия - это линия, соединяющая потребительские наборы, имеющие один и тот же уровень удовлетворения потребностей индивида. По сути дела линии безразличия представляют собой линии уровня функции u = f(x1,x2) или сечения поверхности f(x1,x2) плоскостями, параллельными плоскости х1Oх2; уравнения линий безразличия: (9) u(x1,x2) = const Множество линий безразличия называется картой линий безразличия (карта линий уровня - это снесенные на плоскость х1Oх2 линии уровня, соответствующие различным значениям постоянной величины в правой части (9)). Карта линий безразличия изображается на плоскости х1Oх2 в виде семейства кривых. Понятие линий безразличия и оперирование с ними встречается во многих экономических приложениях, имеющих цель оптимизации экономических процессов. В случае многомерной функции полезности (2), определенной в пространстве много мерных наборов (1), аналогичным образом можно ввести в рассмотрение поверхность безразличия - поверхность уровня функции (2) или гиперповерхность размерностип-1. Укажем основные свойства линий безразличия: Линии безразличия, соответствующие разным уровням удовлетворения потребностей, не касаются и не пересекаются. Это следует из вида их определения (9). (10) (11) Линии безразличия убывают. Рассмотрим уравнение этой линии в виде х2= φ(х1) которое можно получить из (9). Дифференциал функции вдоль линии уровня равен нулю, т.е. du(x1,x2) = u’1dx1+ u’2dx2= 0, откуда следует, что первая производная функции (10) dx2/dx1 = - и’1/и’2 отрицательна в силу свойства 1 функций полезности (формулы (3)). 3. Линии безразличия выпуклы вниз. Действительно, вторая производная функции (10), согласно правилу дифференцирования частного, вычисляется по формуле: d(dx2/dx1)/dx1 = d2х2/d 2х1 = -(и’’11 и’2 - u’’21 u’1 )/(и’2)2 Нетрудно видеть, что согласно свойствам 2 и 3 функций полезности выражение в правой части этого равенства отрицательно, т.е. график функции (10) является выпуклым вниз.  Характерный вид линии безразличия функции полезности на рис №1. 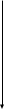  X1, причем C1<C2<C3<C4 X1, причем C1<C2<C3<C4 Из формулы (11) следует важное приближенное равенство -∆x2/∆x1 ≈ - u’1/u’2 Это соотношение показывает, на сколько индивид должен увеличить (уменьшить) потребление второго продукта при уменьшении (увеличении) потребления первого продукта на одну единицу без изменения уровня удовлетворения своих потребностей. Отношение-∆х2/∆x1; называетсянормой замены первого продукта вторым, а величинуdx2 / dx1 - предельной нормой замены первого продукта вторым. Пример: Если предельная полезность первого товара равна 6, а второго - 2, то при уменьшении потребления первого товара на единицу нужно увеличить потребление второго товара на 3 единицы при том же уровне удовлетворения потребностей. Бюджетное множество Пусть р = (р1, р2, …., pn) - вектор цен на набор из n продуктов х. Зафиксируем некоторую денежную сумму I - доход индивида, который он готов потратить на приобретение набора продуктов х принадлежит X (на самом деле это расход индивида на набор продуктов). Множество наборов товаров стоимостью не более I при данных ценах р называется бюджетным множеством (В). При этом множество наборов стоимостью ровно I называется границей G множества В. Таким образом, множество В ограничено границей G, а также естественными ограничениями х ≥ 0. Поскольку граница G определяется соотношением рх = I, то бюджетное множество В описывается системой следующих неравенств: Х ≥ 0, рх ≤ I, (12) или в развернутой форме: xi ≥ 0 (i=1,2,3, ..., п), p1x1 + p2x2 + ...+ pntxn ≤ I (13) Для случая набора из двух товаров бюджетное множество представляет собой треугольник в системе координат х1Ox2 , ограниченный координатными осями и прямойр1x1 + p2x2 = I (Рисунок №2): XI  Задача потребительского выбора (постановка задачи) В теории потребления полагается, что потребитель всегда стремится максимизировать свою полезность и единственным ограничением для него является ограниченность дохода I, который он может потратить на покупку набора товаров. В общем виде задача потребительского выбора (задача рационального поведения потребителя на рынке) формулируется следующим образом: найти потребительский набор (14) x* = (x*1, x*2, ….., x*n), который максимизирует его функцию полезности при заданном бюджетном ограничении. Формальный вид задачи потребительского выбора – ищется точка максимума (14) функции полезности на бюджетном множестве (15) u(x) = u(x1, x2, …., xn) → max; xi ≥ 0 (i = 1, 2, 3, ….., n), p1x1 + p2x2 + …. + pnxn ≤ I (16) Рассмотрим задачу потребительского выбора для случая набора из двух товаров: найти набор x* = (x*1, x*2) такой что u(x) = u(x1, x2) → max; x1 ≥ 0, p1x1 + p2x2 + …. + pnxn ≤ I Поиск оптимального набора х* можно интерпретировать графически как последовательный переход на линии безразличия более высокого уровня полезности (рисунок №3) - вправо - вверх - до тех пор, пока эти линии имеют общие точки с бюджетным множеством. Из геометрии бюджетного множества В и формы линий безразличия следует, что искомая точка (x*1, х*2) лежит на границе G, т.е. на прямой , р1х1 + р2х2 = I . Таким образом, задача потребительского выбора сводится к задаче на условный экстремум - найти точку (x*1, x*2) максимума функции u(x1, x2) при условии, что эта точка находится на прямой p1x1 + p2x2 = I. В условной записи (17) и(х) = u(x1x2) → max; p1x1 + p2x2 = I В общем случае бюджетного множества n-мерных наборов В также справедливо, что точка х* лежит на границе G (на гиперплоскости), определяемой условием рх = I. Поэтому задача потребительского выбора формулируется аналогичным образом в виде задачи на условный экстремум: при заданной функции u(х) и известных векторе р и величине I найти точку такую, что и(х) = и(х1,x2,…..,xn) → max; (18) рх = р1x1 + p2x2 + …. + pnxn = I Последнее уравнение в (18) называется уравнением связи. Рисунок №3: XI 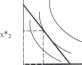 >Х2 |
