математика. Вариант 2. Задача Определить точки пересечения прямой 2х 3у 6 0 с координатными осями и построить эту прямую на чертеже
 Скачать 66 Kb. Скачать 66 Kb.
|
|
Вариант 2 Задача 1. Определить, какие из точек М1(–1; 1), М2(2; 3), М3(6; 3), М4(–4; –1), М5(3; –1), М6(–2; 1) лежат на прямой 2x – 3у + 5 = 0 и какие не лежат на ней. Решение. По определению, если точка лежит на прямой то при подстановке координат точки в уравнение прямой выполняется равенство, в противном случае равенство не выполняется. М1(–1; 1) 2*(-1)-3*1+5=0, равенство истинно, значит точка М1 принадлежит прямой заданной указанным в условии уравнением М2(2;3) 2*2-3*3+5= 0, равенство истинно, значит точка М2 принадлежит прямой заданной указанным в условии уравнением М3(6;3) 2*6-3*3+5 не равно 0, равенство не выполняется, значит точка М3 не принадлежит заданной условием прямой М4(-4;-1) 2*(-4)-3(-1)+5= 0, равенство истинно, значит точка М4 принадлежит прямой заданной указанным в условии уравнением М5(5;3) 2*5-3(-3)+5 не равно 0, М5 не принадлежит М6(-2;-1) 2*(-2)-3*(-1)+5 не равно 0, М6 не принадлежит Ответ: прямой 2x – 3у +5 = 0 принадлежит точки М1, М2, М4, М6. Задача 2. Определить точки пересечения прямой 2х + 3у – 6 = 0 с координатными осями и построить эту прямую на чертеже. Решение. Определим точку пересечения с осью Ох у=0 2х-6=0; х=3; Таким образом имеем точку пересечения с координатами(3;0). Определим точку пересечения с осью Оу х=0 3у-6=2; у=2; координаты точки пересечения 0,2 Построим график функции. Из равнения видно угловой коэффициент 3, проводим прямую с угловым коэффициентом минус три через найденные точки пересечения координатных осей. 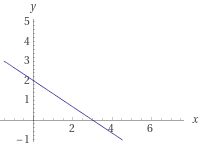 Ответ: (3;0), (0,2). Задача 3. Стороны АВ, ВС и АС треугольника ABC даны соответственно уравнениями 2x + 3у – 5 = 0, 2х – 3у+10 = 0, х – 3 = 0. Определить координаты его вершин. Решение. По определению, точки пересечения прямых, на которых лежат стороны треугольника, являются его вершинами. Найдем координаты этих точек пересечения. - прямых 2x + 3у – 5 = 0(1), 2х - 3у+10 = 0(2), Из (2) х=3/2у-5; в (1) имеем 2*(3/2у-5)-3у-5=0;(3) Решеаем (3) 3у-10+3у-5=0;отсюда у=15/6=2,5 тогда х=3/2*15/6 -5=45/12 -5= -5/4; Имеем координаты точки пересечения (15/6; -5/4). -прямых 2х - 3у+10 = 0, х – 3 = 0. Аналогично х=3, 6 -3у+10=0; х=3, у= 16/3. Имеем координаты точки пересечения (3; 16/3). -прямых 2x + 3у – 5 = 0, х – 3 = 0. Аналогично х=3, 6 + 3у - 5=0; х=3, у= 1/3. Имеем координаты точки пересечения(3; 1/3). 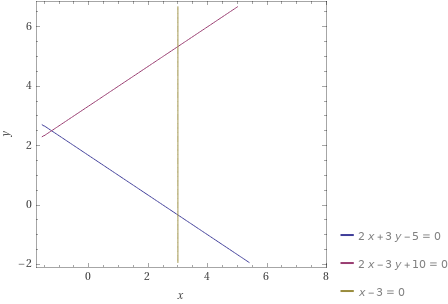 Ответ: (15/6;-5/4), (3; 16/3), (3; 1/3). Задача 4. Составить уравнение прямой и построить прямую на чертеже, зная её угловой коэффициент k и отрезок b, отсекаемый ею на оси Оу: 1) k = 3, b = 3; 2) k = 4, b = 0; 3) k = 0, b = 2; 4) k = -3/2 b = 3; 5) k = 2, b = –5; 6) k = -1/2 b = -1/3 Решение Из условия 1. у=3х+3; 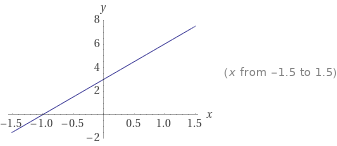 2. у= 4х; 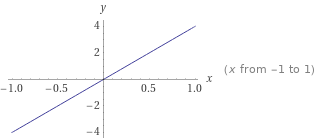 3. у=2; 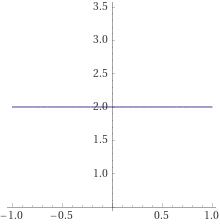 4. у= -3/2 х - 3; 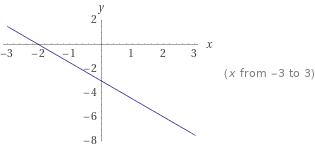 5. у= 2х - 5; 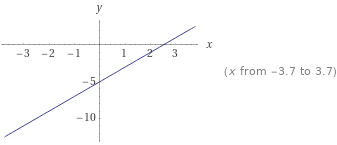 6. у= -1/2 х -1/3. 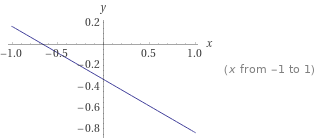 Задача 5. Определить угловой коэффициент k и отрезок b, отсекаемый на оси Оу, для каждой из прямых: 1) 4х – у + 3 = 0; 2) 2х + 5у – 6 = 0; 3) 5х + 2у + 2 = 0; 4) 3x + 4y; = 0; 5) y – 4 = 0. Решение. Из условия, 1. k=4 b=3 2. k= -2/5 b= 3 3. k= -5/2 b= -1 4. k= -3/4 b=0 5. k= 0 b= 4 |
