Задача Пусть даны приближённые значения
 Скачать 175.91 Kb. Скачать 175.91 Kb.
|
|
Задача 1. Пусть даны приближённые значения a и b величин с точными значениями A и B соответственно. Определим, какое из равенств A =a или B = b точнее. Например, определить, какое равенство точнее: 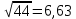 или или 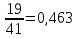 Для решения этой задачи существует следующий алгоритм: 1. Найти приближённые значения a1 и b1 чисел A и B соответственно с большим числом знаков после запятой, чем у a и b. 2. Найти погрешности вычислений a – a1 и b – b1 как разности между двумя приближёнными значениями чисел A и B соответственно. 3. Определить предельные абсолютные погрешности вычислений αAи αBс избытком (округлить полученные значения погрешности вычислений a – a1 и b – b1). 4. Найти предельные относительные погрешности вычислений 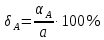 ; ;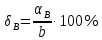 5. Сравнить предельные относительные погрешности вычисления двух чисел, сделать вывод: если A B равенство A=a точнее равенства, B=b; если A B, равенство B=b точнее равенства A=a. Решение: 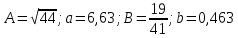 1. Найдём приближённые значения чисел 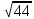 и и 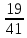 с большим числом десятичных знаков с большим числом десятичных знаковa1 = 6,633 b1 = 0,4634. 2. Определим погрешности вычислений a – a1 и b – b1 a – a1 = 6,63 – 6,633 = – 0,003; b – b1 = 0,463 – 0,4634= – 0,0004. 3. Определим предельные абсолютные погрешности αA и αB с избытком αA = 0,004; αB = 0,0005. 4. Найдём предельные относительные погрешности вычислений 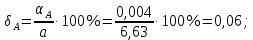 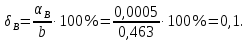 6. Поскольку A B, равенство 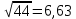 точнее равенства точнее равенства 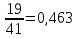 . .Задачи для самостоятельного решения 1. Определить, какое равенство точнее: A=a; B=b. Варианты индивидуальных заданий 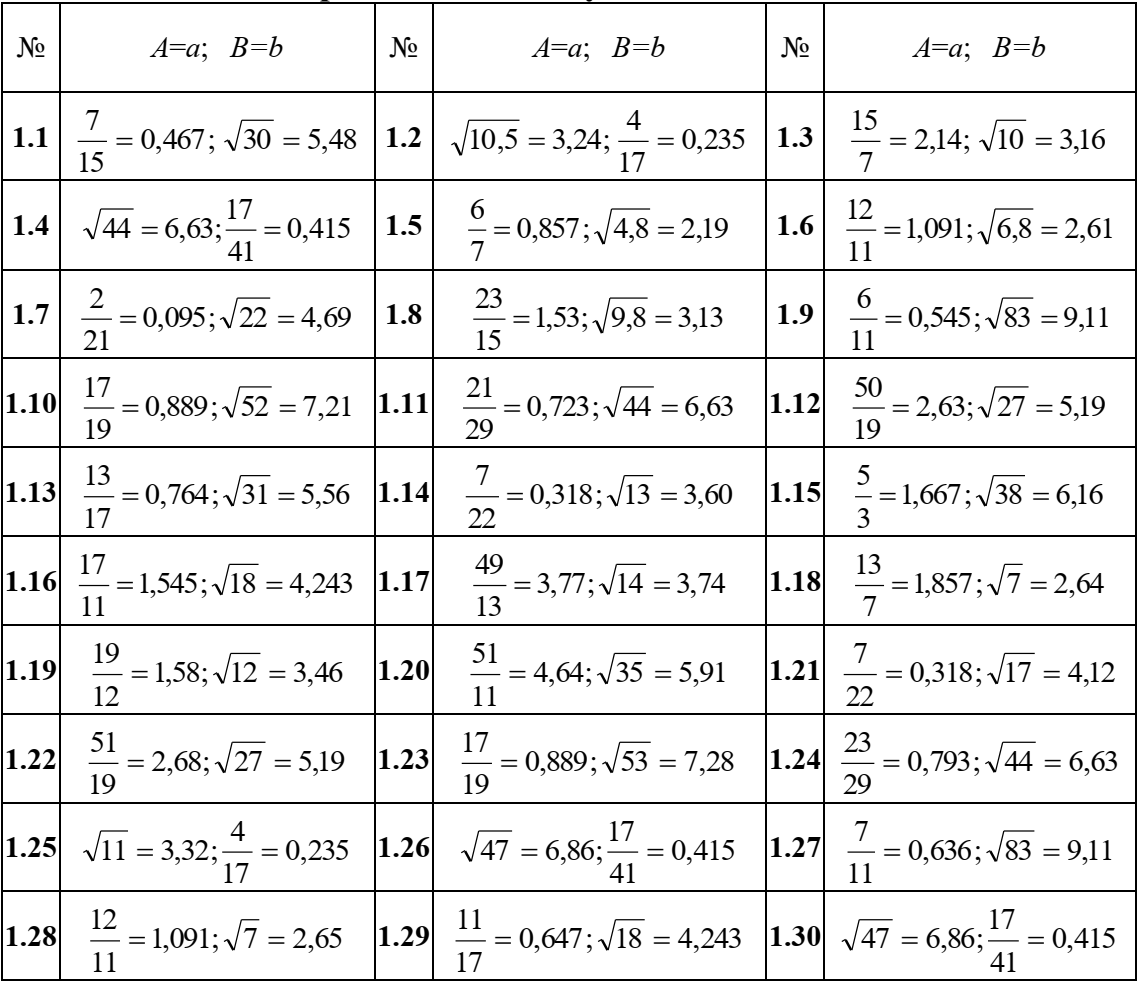 |
