Контрольная 2. Дифференциальное и интегральное исчисления функции одной переменной
 Скачать 269.22 Kb. Скачать 269.22 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное автономное образовательное учреждение высшего образования «Северный (Арктический) федеральный университет имени М.В. Ломоносова» Высшая школа энергетики нефти и газа _____________________________________________________ (наименование высшей школы / филиала / института / колледжа) КОНТРОЛЬНАЯ РАБОТА
Архангельск 2022 Задание 1 8. а) 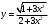 , б) , б) 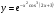 , в) , в) 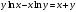 . .Решение а) 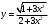 . .Используя правило дифференцирования частного, правило дифференцирования сложной функции и табличные формулы, получим: 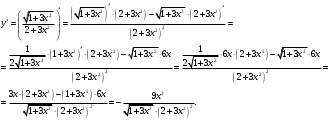 б) 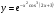 . .Используя правило дифференцирования произведения, правило дифференцирования сложной функции и табличные формулы, получим: 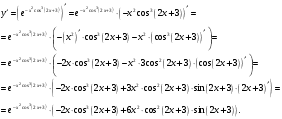 в) 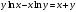 . .Функция задана неявно в виде 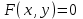 . .Дифференцируем обе части данного уравнения, считая 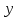 функцией от функцией от 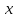 : :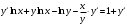 Выразим из уравнения 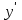 : :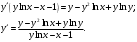 Задание 2 Исследовать методами дифференциального исчисления функцию и построить ее график, используя результаты исследования. 8. 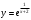 Решение Для полного исследования функции и построения ее графика применяется следующая примерная схема: найти область определения функции; исследовать функцию на непрерывность и определить характер точек разрыва; исследовать функцию на четность и нечетность, периодичность; найти точки пересечения графика функции с осями координат; исследовать функцию на монотонность и экстремум; найти интервалы выпуклости и вогнутости, точки перегиба; найти асимптоты графика функции; по полученным данным построить график функции. Применим вышеуказанную схему для исследования данной функции. 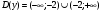 . .Функция не определена в точке 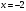 . Следовательно, . Следовательно, 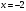 есть точка разрыва функции. Исследуем характер точки разрыва, для чего найдем односторонние пределы функции в этой точке: есть точка разрыва функции. Исследуем характер точки разрыва, для чего найдем односторонние пределы функции в этой точке: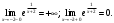 Следовательно, 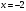 – точка разрыва второго рода; – точка разрыва второго рода;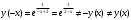 .Функция не является ни четной, ни нечетной. Функция не периодическая. .Функция не является ни четной, ни нечетной. Функция не периодическая.С осью Ох точек пересечения нет. С осью Оу: 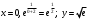 . .Точка 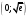 – точка пересечения с осью Оy. – точка пересечения с осью Оy.Находим производную. 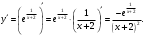 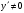 при при 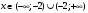 и не существует при и не существует при 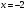 . .Критических точек нет. 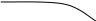     – – – –  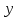 –2 –2 Функция убывает на всех 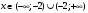 . .Находим вторую производную. 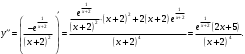 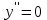 при при 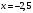 и не существует при и не существует при 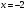 . .Критическая точка второго рода: 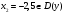 . .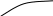   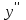 - + + - + +      -2,5 -2 -2,5 -2 Функция вогнута на интервалах 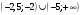 , функция выпукла на интервале , функция выпукла на интервале 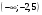 . .Точка перегиба 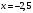 , , 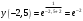 . .Так как точка 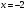 - точка разрыва второго рода, то прямая - точка разрыва второго рода, то прямая 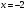 - вертикальная асимптота. - вертикальная асимптота.Найдем наклонные асимптоты 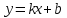 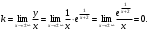 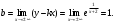 Тогда 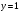 - горизонтальная асимптота - горизонтальная асимптотаПо полученным данным строим график функции. 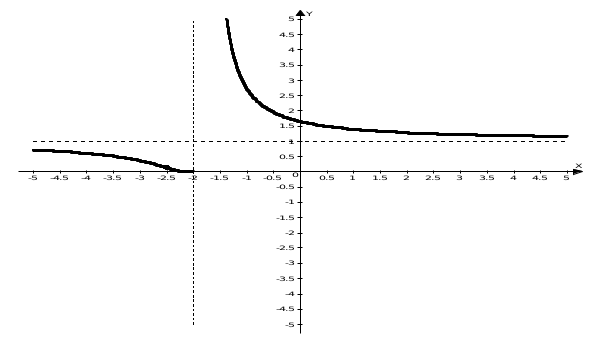 Задание 3 Найдите неопределенные интегралы. В п. а) и б) результаты проверить дифференцированием. 8. а) 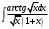 ; б) ; б)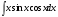 ; ;в) 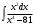 ; г) ; г) 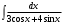 . .Решение а) 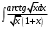 . .Применим подстановку 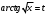 : :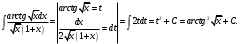 Проверка: 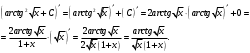 б) 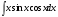 ; ;Применим формулу интегрирования по частям 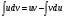 . . 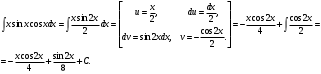 Проверка: 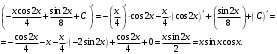 в) 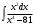 . .Разложим подынтегральную дробь на сумму простейших дробей: 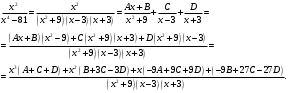 Коэффициенты 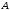 , ,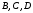 найдем из условия: найдем из условия: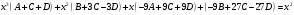 . . Приравняем коэффициенты с одинаковыми степенями при x: 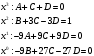 откуда откуда 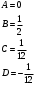 Таким образом, 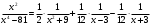 . .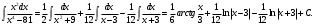 г) 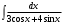 ; ;Для преобразования подынтегральной функции применим формулы универсальной тригонометической подстановки 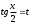 . . 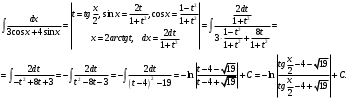 Задание 4 Вычислите определенные интегралы. 8. 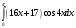 . .Решение Находим интеграл с помощью формулы интегрирования по частям 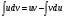 и применим формулу Ньютона-Лейбница: и применим формулу Ньютона-Лейбница: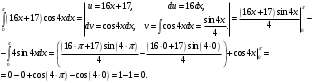 Ответ: 0. Задание 5 Найдите общее решение дифференциального уравнения. 8. а) 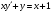 ; б) ; б) 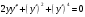 . .Решение а) 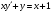 . .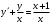 Это линейное дифференциальное уравнение первого порядка. Будем искать решение в виде 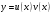 , тогда , тогда 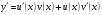 . После подстановки . После подстановки 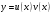 и выражения для производной в уравнение получим и выражения для производной в уравнение получим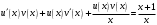 . .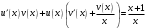 . .Потребуем: 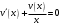 . .Получаем систему: 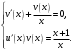 Решим уравнение 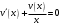 . .Получаем: 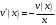 . .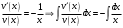 . .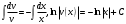 . .откуда при C =0: 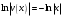 и искомая функция будет иметь вид: и искомая функция будет иметь вид: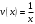 . .После подстановки функции 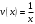 во второе уравнение, получим во второе уравнение, получим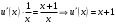 . Решим последнее уравнение: . Решим последнее уравнение: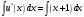 , ,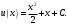 Тогда 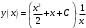 – общее решение исходного уравнения. – общее решение исходного уравнения.б) 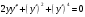 . .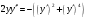 . .Имеем дифференциальное уравнение второго порядка, допускающее понижение порядка, так как не содержит  Введем подстановку: 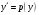 , , 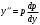 . .Получаем: 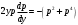 . .Получаем: 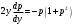 Разделяя переменные, последовательно находим: 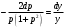 ; ; 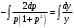 ; ; 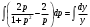 ; ; 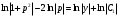 ; ; 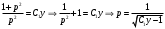 С учетом подстановки: 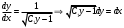 . .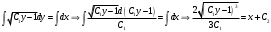 – общий интеграл. – общий интеграл.При решении было упущено решение: 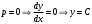 . .Задание 6 Решите задачу Коши 8. 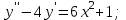  Решение. Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Общее решение y(x) исходного линейного неоднородного дифференциального уравнения имеет вид: 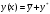 , , где 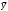 – общее решение соответствующего однородного уравнения, – общее решение соответствующего однородного уравнения,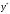 – частное решение исходного неоднородного уравнения. – частное решение исходного неоднородного уравнения.1) Найдем 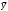 – общее решение соответствующего однородного уравнения, т.е. уравнения: – общее решение соответствующего однородного уравнения, т.е. уравнения: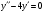 Для этого составляем характеристическое уравнение: 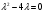 Получаем: 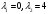 . . Эти корни являются действительными разными, поэтому система решений, соответствующая этим корням, будет иметь вид: 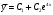 . .2) Найдем 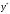 – частное решение исходного неоднородного уравнения. – частное решение исходного неоднородного уравнения.Частное решение неоднородного уравнения будем искать в виде 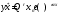 . .В нашем случае 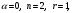 так как так как 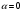 один раз встречается среди корней характеристического уравнения. один раз встречается среди корней характеристического уравнения.Итак, 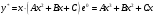 , где , где 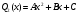 это многочлен второй степени. это многочлен второй степени. Находим: 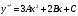 . .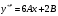 . .Подставляем в исходное уравнение: 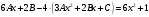 . .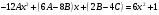 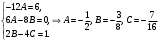 . .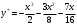 . .Общее решение y(x) исходного линейного неоднородного дифференциального уравнения имеет вид: 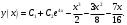 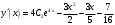 Воспользуемся начальными условиями:  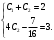 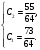 Тогда искомое частное решение: 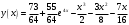 . .Ответ: 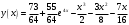 . . | |||||||||||||||||||||||||||||||||||||||||||||||||||
