Математика. РГР Математика Сырчин 9ОПба-3. Задача 20 Найти производные данных функций б По формуле Сначала прологарифмуем
 Скачать 65.17 Kb. Скачать 65.17 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Комсомольский-на-Амуре государственный университет» Факультет авиационной и морской техники Кафедра «Высшая математика» РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №2 по дисциплине «Математика» «Дифференциальное исчисление функции одной и нескольких переменных» Вариант № 0 Студент группы 9ОПба-3 А. С. Сырчин Преподаватель Н. Л. Катунцева 2020 Задача 20: Найти производные данных функций: 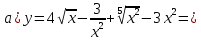 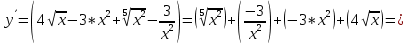 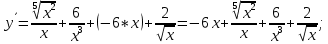 б) 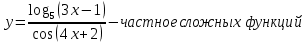 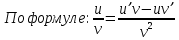 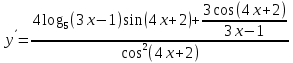 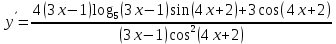 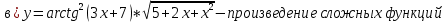 По формуле: 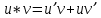 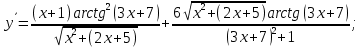 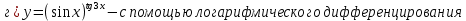 Сначала прологарифмуем: 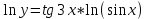 Теперь найдём производную функции, заданную неявно: 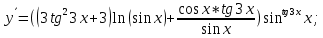 д) 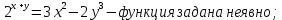 Найдём производную, зная, что у сложная функция, зависящая от х: 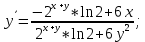 Задача 30: Найти 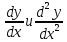 для функций: для функций:а) 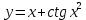 Найдем производные первого и второго порядков: 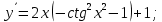 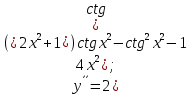 б) 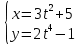 Функция задана параметрически, где: 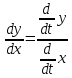 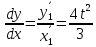 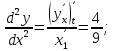 Задача 40: Найти: а) дифференциал; б) приближенное значение заданной величины с помощью дифференциала 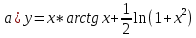 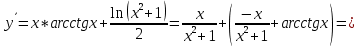 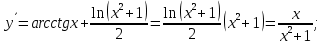 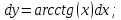 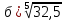 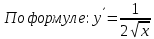 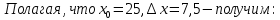 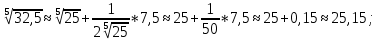 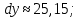 Задача 50: Найти наибольшее и наименьшее значение функции y=f(x) на отрезке 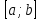 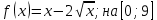 Найдем значения функций на концах отрезка: 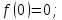 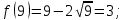 Найдем производную: 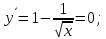 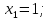 Таким образом: 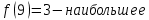  Задача 60: Найти 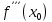 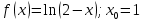 Найдем производную первого порядка: 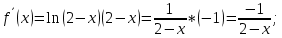 Найдем производную второго порядка: 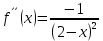 Найдем производную третьего порядка: 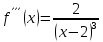 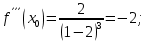 Задача 80: Исследовать и построить график функции: 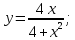 ООФ: 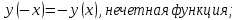 Пересечение с осью Оу - x=0, y=0; Пересечение с осью Ох- y=0; 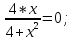 x1=0;  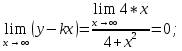 y=0 – горизонтальная асимптота; Найдем первую производную: 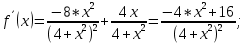 Отсюда: 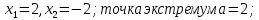 Найдём производную второго порядка: 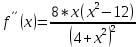 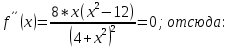 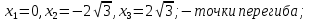 Построим искомый график: 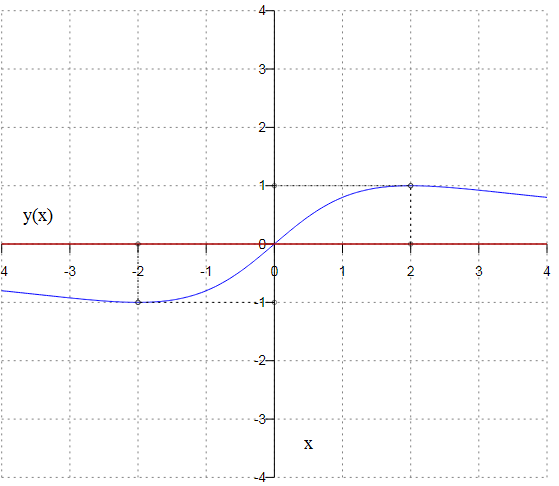 Задача 10: Проверить, удовлетворяет ли указанному уравнению данная функция: 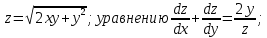 Найдем частные производные: 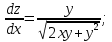 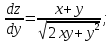 Подставим: 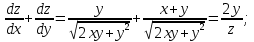 Тождество выполняется. Задача 20: Вычислить приближенно данные выражения, заменив приращения соответствующих функций их полными дифференциалами. Оценить в процентах возникающую при этом относительную погрешность вычислений. 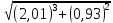 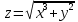 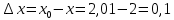 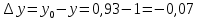 Найдем частные производные: 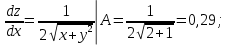 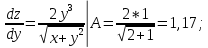 Приращение: 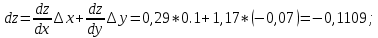 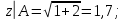 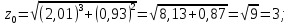 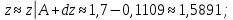 Погрешность: 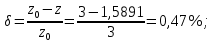 Задача 30: Задана функция 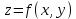 1) исследовать на экстремум 2) найти наибольшее и наименьшее значения функции в замкнутой области D, ограниченной заданными линиями. Сделать чертеж. 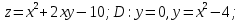 1) 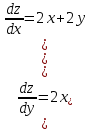 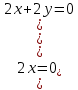 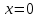 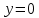 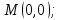 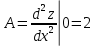 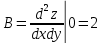 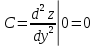 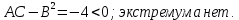 2) 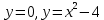 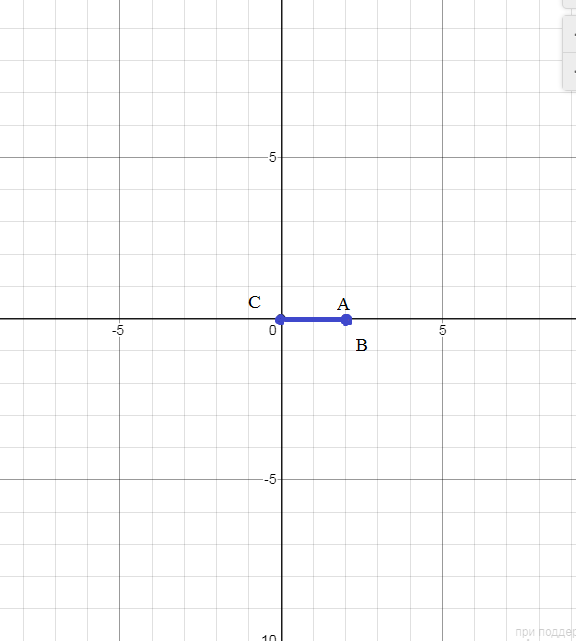 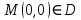 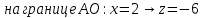 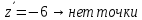 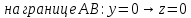 |
