ДЗ по Физике Задача 3-3 (Варианты 9-20). Задача 33 для вариантов с 9 по 20
 Скачать 126.29 Kb. Скачать 126.29 Kb.
|
|
Задача 3-3 для вариантов с 9 по 20 Каждая колебательная система (КС), представленная на рис. 28, 29, 30, 31, состоит из шайбы массой m и двух упругих пружин, имеющих жесткости k1 и k2 . Движение КС происходит в окружающей среде с малыми вязкими свойствами (малым коэффициентом сопротивления r). На рис. 28, 30 шайба колеблется под действием пружин, соединенных параллельно, а на рис. 29, 31 колебания происходят под действием пружин, соединенных последовательно. Массой пружин можно пренебречь. На рис. 28, 29 КС имеет горизонтальное расположение, а на рис. 30, 31 вертикальное расположение в поле силы тяжести. Длины 1-ой и 2-ой пружин в недеформированных состояниях равны l10 и l20. На рис.28, 30 L - длина каждой пружины в деформированном состоянии при t=0. На рис.29, 31 L - общая длина двух пружин в деформированном состоянии при t=0. Возможные векторы начальной скорости шайбы равны V1, V2. Шайбу, находящуюся в положении равновесия, смещают до расстояния L, а затем импульсом придают ей в начальный момент времени t=0 скорость V1 или V2 , в соответствии с заданием (см. таблицы №10 - 13). В результате КС приходит в колебательное движение. Общие исходные данные: 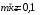 , , 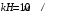 , , 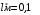 , , 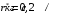 , , 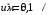 , , 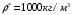 , , 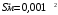 , , 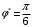 . .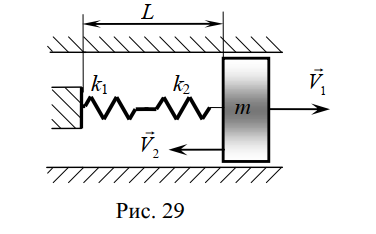
Решение 1. 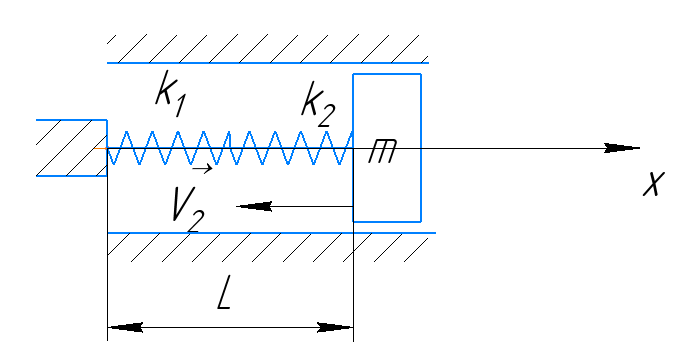 По второму закону Ньютона 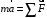 (1) (1)Проецируя (1) на ось x 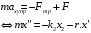 (2) (2)где: x2 – изменение длины второй пружины. Так как две пружины соединяются последовательно 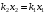 (3), где x1 – изменение длины первой пружины (3), где x1 – изменение длины первой пружиныКроме того, имеем 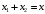 (4) (4)Из (3) и (4) 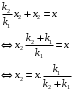 (5) (5)Из (2) и (5) 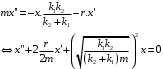 (6) (6)Дифференциальное уравнение свободных затухающих колебаний запишется так: 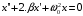 (7) (7)Где: 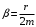 - коэффициент затухания, - коэффициент затухания, 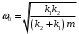 - круговая частота свободного незатухающего колебания - круговая частота свободного незатухающего колебанияТогда период свободного незатухающего колебания равен 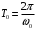 (8) (8)Круговая частота 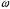 и период T свободного затухающего колебания и период T свободного затухающего колебания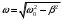 (9) (9)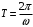 (10) (10)Логарифмический декремент затухания вычисляется по формуле 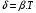 (11) (11)Решение уравнения (7) при 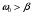 имеет вид имеет вид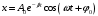 (12) (12)Из (12) 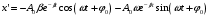 (13) (13)В начальный момент времени 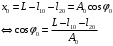 (14) (14)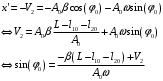 (15) (15)Из (14), (15) и 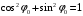 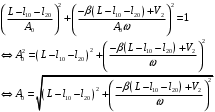 (16) (16)Из (14) 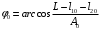 (17) (17)При 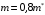 , , 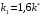 , ,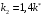 , , 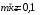 , , 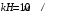 , , 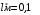 , , 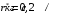 , , 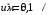 , ,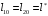 , , 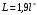 , ,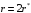 , , 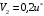 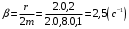 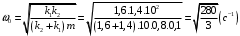 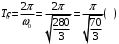 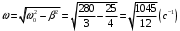 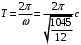 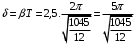 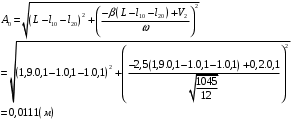 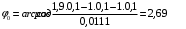 Уравнение колебания 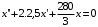 Его решение 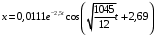 |
