Задача 65 Шаровая заглушка радиусом

• Название: Задача 65 Шаровая заглушка радиусом
• Дата: 26.05.2022
• Размер: 92.61 Kb.
• Имя файла: 4626566.docx
• Тип: Задача; #550724

Задача 3.65

Шаровая заглушка радиусом R запирает отверстие диаметром d в вертикальной стенке сосуда.

Определить наименьший уровень воды в сосуде, при котором стальной шар ( 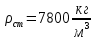) радиусом R = 100 мм еще будет находиться в равновесии.

d = 1,5R, p = 0,1 ати.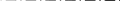



p


H

R

d

Решение

Так как в условии задачи не оговорено, какое давление над свободной поверхностью воды в сосуде, то будем считать его избыточным (манометрическим), т.е. р = р_изб = 0,1 ати = 9810 Па.

Определим вес шара

G =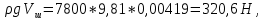

где V_ш =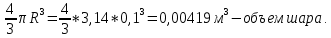

Определим смоченный объем шара

V_ABCMA = V_ш – V_AKCMA= 0,00419 – 0,00032 = 0,00387 м³,

где объем сегмента V_AKCMA определим по формуле

V_AKCMA = 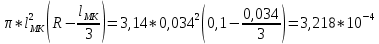м³.

Значение l_MK определяли следующим образом (рис. 1):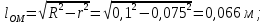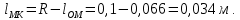





где r = 0,5d = 0,75R = 0,075 м.



H A

R r

у B O M K d = 0,15 м

P_г

C

Рис. 1. Расчетная схема к решению задачи

Горизонтальную составляющую силы гидростатического давления определим из выражения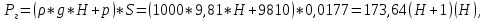



где S = 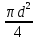= = 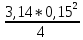0,0177 м² – площадь отверстия.

Определим координату центра давления (точку приложения силы Р_г)

у = 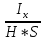= = 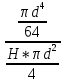= = 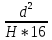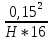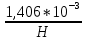м.

В виду того, что значение у очень мало, считаем, что сила P_г приложена к центру сечения.

Вертикальная составляющая силы гидростатического давления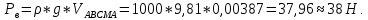



Для определения искомой величины H запишем условие равновесия шара относительно точки С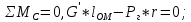



Здесь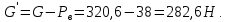

Тогда получим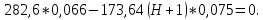



Отсюда определим искомую величину Н

H = 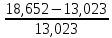= 0,43 м.

Ответ: H = 0,43 м.