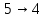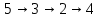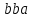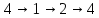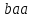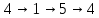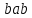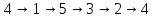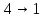Дискретная математика (Задача 7, вариант 4). Задача 7, вариант 4. Задача 7 Автомат задан набором где алфавит, множество начальных состояний, входов
 Скачать 54.5 Kb. Скачать 54.5 Kb.
|
|
Вариант 4 Задача 7 Автомат задан набором 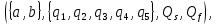 где 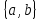 - алфавит, - алфавит, 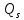 - множество начальных состояний, входов, - множество начальных состояний, входов,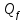 - множество конечных состояний, выходов, и списком дуг с метками , определяющих допустимые переходы. Запись - множество конечных состояний, выходов, и списком дуг с метками , определяющих допустимые переходы. Запись 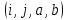 означает, что дуга означает, что дуга 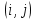 , идущая из состояния , идущая из состояния 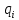 , в состояние , в состояние 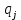 , имеет две метки - , имеет две метки - 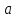 и и 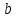 . .Построить граф автомата и найти язык 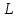 , допускаемый автоматом. , допускаемый автоматом.Детерминизировать автомат. Построить графы автоматов, представляющих языки 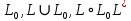 . .Из построенных графов удалить 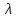 - переходы . - переходы .Вход 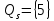 , выход , выход 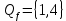 , дуги , дуги 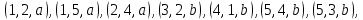 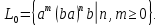 Решение: Граф автомата 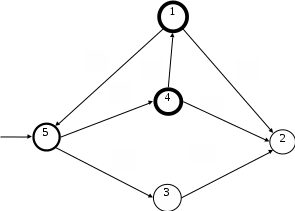 Толстой линией обозначено начальное состояние, двойной линией обозначены конечные состояния. Найдём язык, который распознаётся данным автоматом, составим таблицу возможных переходов между состояниями автомата и соответствующих последовательностей символов,
в таблице приведены последовательности символов, из которых строятся слова языка 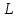 , , 2 – наименьшие возможные слова языка 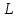 , также любое слово будет начинаться с этих последовательностей, , также любое слово будет начинаться с этих последовательностей, 1- 2 - возможные слова языка 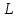 , последовательности символов до перехода в состояние 4, , последовательности символов до перехода в состояние 4,3 - 5 - возможные повторяющиеся последовательности символов, последовательности могут повторяться в любом количестве и в любом порядке, 6 - возможные окончания слова, если слово заканчивается в состоянии 1, 2 - последовательности, которые также являются словами языка 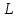 , , для языка 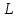 получаем следующее представление, получаем следующее представление,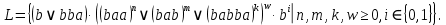 Данный автомат недетерминированный, так как есть из одного состояния при прочтении символа есть неоднозначные переходы, например, из состояния 1 при прочтении 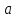 возможен переход в состояния 2 и 5, возможен переход в состояния 2 и 5,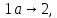 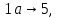 из состояния 5 при прочтении 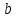 возможен переход в состояния 3 и 4, возможен переход в состояния 3 и 4,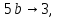 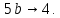 Найдем эквивалентный детерминированный автомат. Представим все возможные переходы автомата в виде таблицы, в которой каждому состоянию соответствует строка, каждому символу алфавита соответствует столбец, на пересечении строки и столбца, соответствующего символу алфавита указываются состояния, в которые переходит автомат из данного состояния при прочтении данного символа, в последнем столбце указано, является ли данное состояние конечным, 0 – состояние не является конечным, 1 – состояние является конечным,
построим детерминированный автомат, первая строка таблицы записывается без изменений, следующими в качестве состояний записываются состояния и множества состояний, в которые переходит первое состояние, далее в качестве состояний записываются состояния и множества состояний, в которые переходят предыдущие состояния и множества состояний, и так пока все состояния и множества состояний, в которые переходят предыдущие состояния и множества состояний, не будут перечислены в таблице, получаем таблицу
Создадим обозначения для новых состояний , представленных множествами состояний, и запишем обозначения в 5-й столбец таблицы,
запишем автомат с использованием новых обозначений,
Построим граф детерминированного автомата 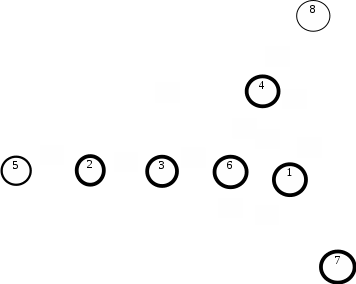 толстой линией обозначено начальное состояние, двойной линией обозначены конечные состояния. Построим граф детерминированного автомата, представляющего язык 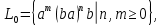 граф детерминированного автомата, представляющего язык 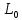 , ,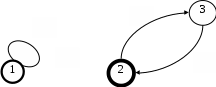 Построим графы автоматов, представляющих объединение языков 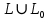 , ,конкатенацию языков 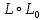 и итерацию языка и итерацию языка 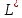 , ,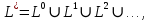 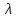 - пустое слово, - пустое слово, 0 – начальное состояние, для того, чтобы не возникало неоднозначности в обозначении состояний автоматов, будем обозначать состояния автомата, представляющего язык 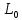 9 - 11 , то есть к каждому обозначению состояния автомата для 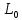 прибавим 8 . Новые переходы будем обозначать цветными стрелками, 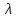 – переходы будем обозначать синими и зелёными стрелками , – переходы будем обозначать синими и зелёными стрелками ,при удалении 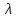 – переходов – переходовпереходы, если прочитаны символы 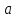 или или 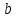 будем обозначать зелёными и фиолетовыми стрелками. будем обозначать зелёными и фиолетовыми стрелками.Построим граф автомата, представляющего объединение языков 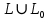 , ,обозначим в виде прямоугольников графы автоматов , представляющих языки 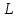 и и 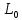 , тогда граф автомата, представляющего объединение языков , тогда граф автомата, представляющего объединение языков 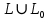 может быть представлен в виде, может быть представлен в виде,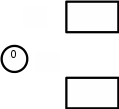 Граф автомата, представляющего объединение языков 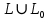 , ,  Построим граф автомата, представляющего конкатенацию языков 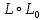 , ,обозначим в виде прямоугольников графы автоматов , представляющих языки 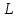 и и 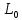 , тогда граф автомата, представляющего конкатенацию , тогда граф автомата, представляющего конкатенацию языков 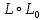 может быть представлен в виде, может быть представлен в виде,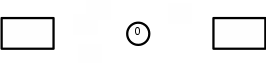 Граф автомата, представляющего конкатенацию языков 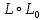 , ,  Построим граф автомата, представляющего итерацию языка 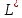 , ,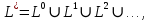 обозначим в виде прямоугольника граф автомата , представляющего язык 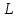 , тогда граф автомата, представляющего итерацию языка , тогда граф автомата, представляющего итерацию языка 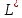 , может быть представлен в виде, , может быть представлен в виде,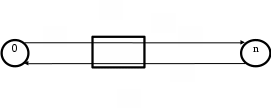 Граф автомата, представляющего итерацию языка 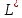 , ,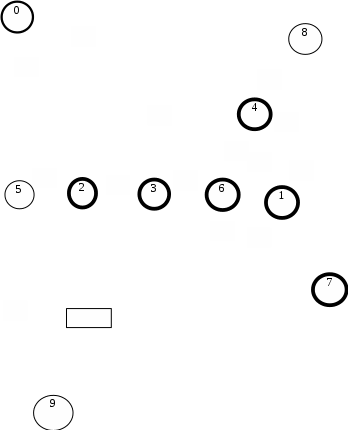 Из построенных графов автоматов, представляющих объединение языков 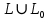 , , конкатенацию языков 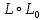 и и итерацию языка 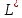 , , удалим 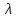 - переходы . - переходы .Граф автомата, представляющего объединение языков 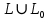 , ,  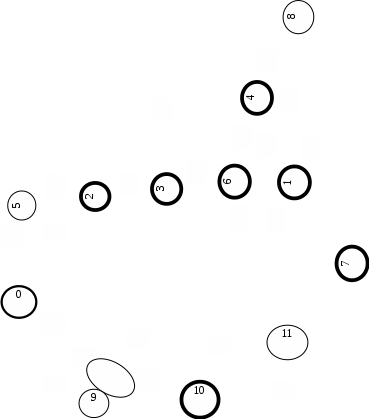 граф автомата, представляющего объединение языков 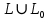 без 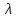 – переходов , – переходов , 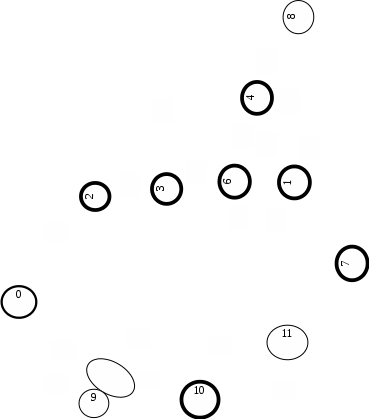 Граф автомата, представляющего конкатенацию языков 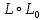 , ,  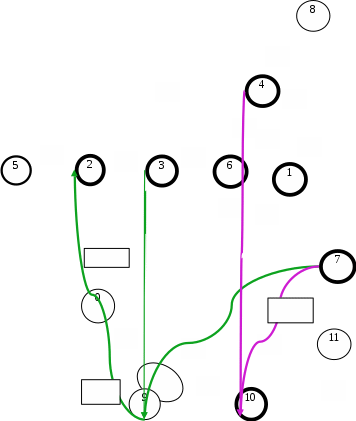 . граф автомата, представляющего конкатенацию языков 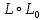 без 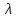 – переходов , – переходов ,  Граф автомата, представляющего итерацию языка 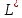 , ,  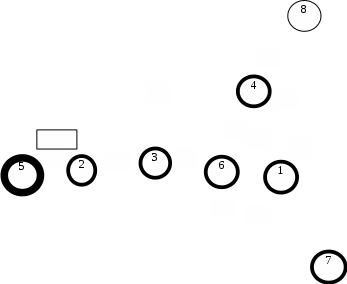 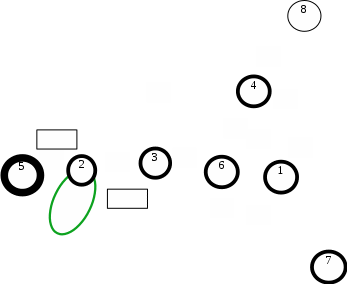 граф автомата, представляющего итерацию языка 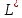 без без 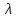 – переходов , – переходов ,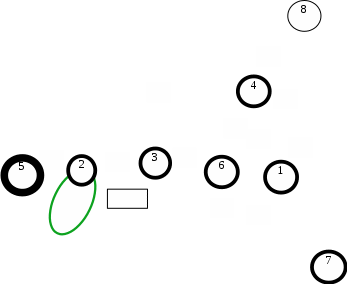 |