Задача 7 Условие
 Скачать 135.6 Kb. Скачать 135.6 Kb.
|
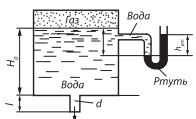
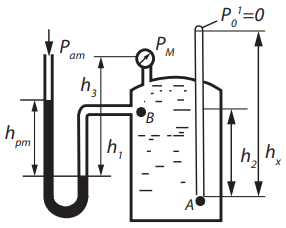
Задача № 1.7Условие: Закрытый резервуар с керосином снабжен закрытым пьезометром, дифференциальным ртутным и механическим манометрами. Определить высоту поднятия ртути hрт в дифференциальном манометре и пьезометрическую высоту hx в закрытом пьезометре, если показания манометра рм = 0,12 МПа, а расстояния между точками соответственно равны: h1 = 1,3 м, h2 = 2,3 м, h3 = 2,0 м. Решение: Дано:
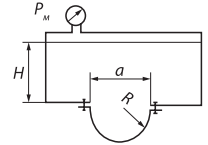
Давление в точке В: 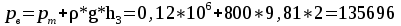 Па. Па.Давление в точке А: 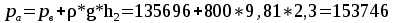 Па. Па.Определяем высоту hx из уравнения равновесия: 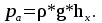 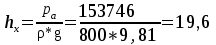 м. м.Определяем hрт: 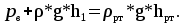 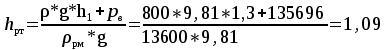 м. м.Ответ: hрт – 1,09 м; hх – 19,6 м. Задача № 2.8 Условие: В дне призматического резервуара с бензином имеется прямоугольное отверстие a * b = 1 * 2 м, перекрытое полуцилиндрической крышкой радиусом R = 0,5 м. Определить усилие, воспринимаемое болтами крышки, если уровень бензина Н = 3,5 м, а давление паров бензина рм = 18 кПа. Решение: Дано:
Вертикальная составляющая силы давления на криволинейную поверхность равна весу жидкости в объеме тела давления: 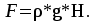 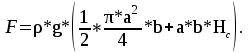 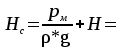 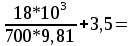 6,12 м. 6,12 м.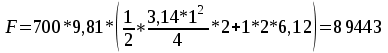 Н. Н.Ответ: F = 89 кН. Задача № 3.7Условие: Определить расход воды, вытекающей из бака через короткую трубу (насадок) диаметром d = 30 мм и коэффициентом сопротивления ξ = 0,5, если показание ртутного манометра hрт = 1,47 м; H1 = 1 м; H0 = 1,9 м; l = 0,1 м. Решение: Дано:
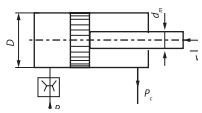
Избыточное давление газа в баке: 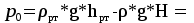 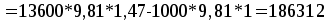 Па. Па.Составим уравнение Бернулли для сечений 1-1 и 2-2: 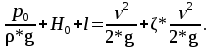 Отсюда найдем скорость истечения из бака: 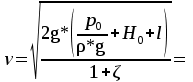 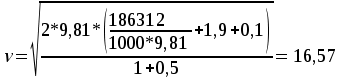 м/с. м/с.Расход воды: 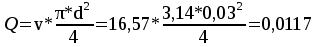 м³/с = 11,7 л/с. м³/с = 11,7 л/с.Ответ: Q = 11,7 л/с. Задача № 4.8Условие: Определить значение силы F, преодолеваемой штоком гидроцилиндра при движении его против нагрузки со скоростью υ = 20 мм/с. Давление на входе в дроссель pН = 20 МПа; давление на сливе pс = 0,3 МПа; коэффициент расхода дросселя μ = 0,62; диаметр отверстия дросселя d = 1,2 мм; D = 70 мм; dШ = 30 мм; ρ = 900 кг/м3. Решение: Дано:
Расход через дроссель равен: 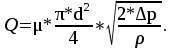 С другой стороны, расход через дроссель также равен: 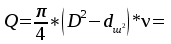 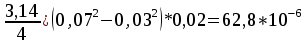 м³/с м³/сНайдем Δр: 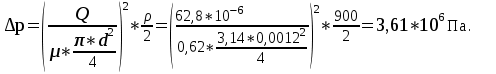 Находим давление слева от поршня: 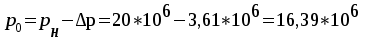 Па. Па.Находим значение силы F из уравнения равновесия: 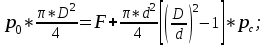 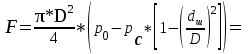 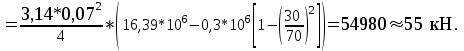 Ответ: F = 55 кН. Задача № 5.7Условие: На рисунке показан сложный трубопровод. Определить расходы в каждом из простых трубопроводов, если их длины соответственно равны: l1 = 5 м, l2 = 3 м, l3 = 3 м, l4 = 6 м, а суммарный расход Q = 6 л/мин. Считать, что режим течения ламинарный, а диаметры трубопроводов одинаковы. Решение: Дано:
В узле A поток с расходом Q0 разделяется на два потока с расходами Q1 и Q2: 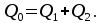 В узле B поток с расходом Q2 разделяется на два потока с расходами Q3 и Q4: 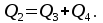 Суммарные потери на участке B-C, состоящем из параллельно соединенных 3 и 4 участков, равны потерям на каждом из них: 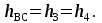 Потери на участке A-C равны потерям в 1 трубопроводе или сумме потерь на участке A-B во втором трубопроводе и потерь на участке B-C: 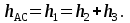 По условию задачи режим течения в подводящем трубопроводе ламинарный, следовательно, на всех участках режим также ламинарный. При ламинарном режиме течения потери на трение по длине определяются по формуле Пуазейля: 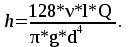 Учитывая, что на всех участках трубопровода диаметр одинаковый, можно записать 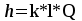 . Выразив потери через соответствующие длины и расходы, получаем систему из 4 уравнений с 4 неизвестными: . Выразив потери через соответствующие длины и расходы, получаем систему из 4 уравнений с 4 неизвестными: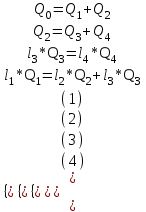 Из (1) получаем (5): 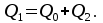 Подставив (5) в (4) имеем (6): 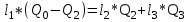 или или 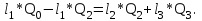 Из (3) следует, что: 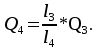 Выразив Q2 в (2) через 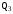 , имеем (7): , имеем (7):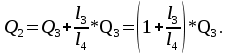 После подстановки (7) в (6) получим: 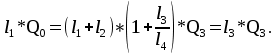 Откуда 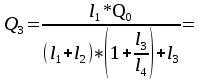 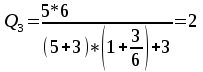 л/мин; л/мин;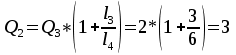 л/мин; л/мин;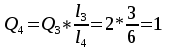 л/мин; л/мин;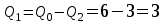 л/мин. л/мин.Ответ: Q1 = 3 л/мин; Q2 = 3 л/мин; Q3 = 2 л/мин; Q4 = 1 л/мин. |

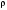 = 800 кг/м3
= 800 кг/м3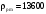 кг/м3
кг/м3