Надежность, эргономика и качество автоматизированных систем обработки информации и управления. Надежность, эргономика и качество автоматизированных систем обра. Задача 8
 Скачать 206.34 Kb. Скачать 206.34 Kb.
|
|
Вариант 8 Задача 1.8 На испытание поставлено 400 резисторов. За время наработки 10000 час отказало 4 резистора. За последующие 1000 час отказал еще 1 резистор. Определить частоту и интенсивность отказов резисторов в промежутке времени 10000 – 11000 час. Найдем частоту отказов по формуле: 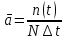 где 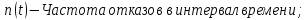 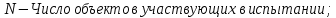 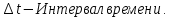 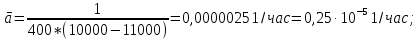 Найдем интенсивность отказов по формуле: 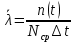 где 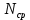 – Среднее число объектов, исправно работавших в интервале времени; – Среднее число объектов, исправно работавших в интервале времени;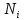 – Число изделий, работавших в начале интервала Δt; – Число изделий, работавших в начале интервала Δt;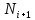 – Число объектов, исправно работавших в конце интервала времени Δt. – Число объектов, исправно работавших в конце интервала времени Δt.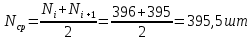 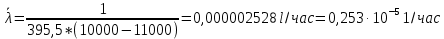 Ответ: 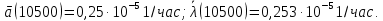 Задача 1.28 На испытание поставлено 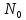 изделий. За время t час вышло из строя изделий. За время t час вышло из строя 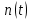 штук изделий. За последующий интервал времени штук изделий. За последующий интервал времени 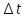 вышло из строя вышло из строя 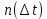 изделий. Необходимо вычислить вероятность безотказной работы за время t и t+ изделий. Необходимо вычислить вероятность безотказной работы за время t и t+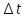 , частоту отказов и интенсивность отказов на интервале , частоту отказов и интенсивность отказов на интервале 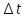 . . Вероятность безотказной работы вычислим по формуле: 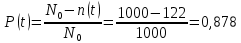 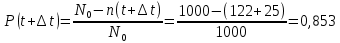 Найдем частоту отказов по формуле: 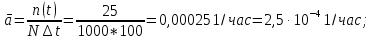 Найдем интенсивность отказов по формуле: 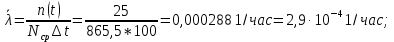 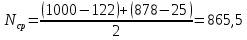 Ответ: 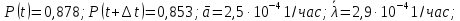 Задача 1.108 В течение времени 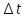 производилось наблюдение за восстанавливаемым изделием и было зафиксировано производилось наблюдение за восстанавливаемым изделием и было зафиксировано 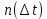 отказов. До начала наблюдения изделие проработало отказов. До начала наблюдения изделие проработало 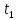 [час], общее время наработки к концу наблюдения составило [час], общее время наработки к концу наблюдения составило 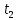 [час]. Требуется найти наработку на отказ. [час]. Требуется найти наработку на отказ. Найдем наработку на отказ по формуле: 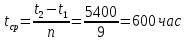 Ответ: 600 час Задача 1.123 В течение некоторого времени производилось наблюдение за работой 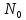 экземпляров восстанавливаемых изделий. Каждый из образцов проработал экземпляров восстанавливаемых изделий. Каждый из образцов проработал 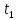 [час], и имел [час], и имел 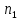 отказов. Требуется определить наработку на отказ по данным наблюдения за работой всех изделий. отказов. Требуется определить наработку на отказ по данным наблюдения за работой всех изделий. 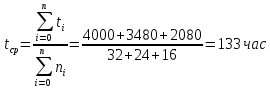 Ответ: 133 час Задача 1.138 Система состоит из N приборов, имеющих разную надежность. Известно, что каждый из приборов, проработав вне системы 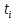 [час], имел [час], имел 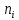 отказов. Для каждого из приборов справедлив экспоненциальный закон надежности. Необходимо найти наработку на отказ всей системы. отказов. Для каждого из приборов справедлив экспоненциальный закон надежности. Необходимо найти наработку на отказ всей системы. 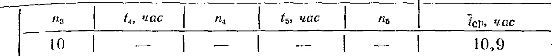 Найдем наработку на отказ всей системы по формуле: 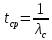 Где 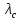 — интенсивность отказа системы. — интенсивность отказа системы.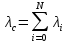 Где 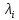 — интенсивность i – го прибора. — интенсивность i – го прибора.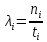 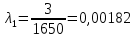 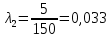 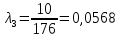 Тогда 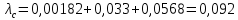 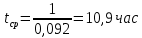 Ответ: 10,9 час. Задача 1.167 Используя данные задачи 1.166 вычислить частоту отказов шарикоподшибников для времени t = 150 час. Задача 1.166: «Время исправной работы скоростных шарикоподшибников подчинено закону Вейбулла с параметрами a = 2,6; 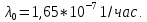 Необходимо найти вероятность безотказной работы шарикоподшибника в течение 150 час» Необходимо найти вероятность безотказной работы шарикоподшибника в течение 150 час»Частоту отказов найдем через произведение интенсивности отказов на : 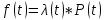 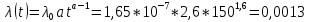 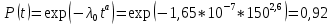 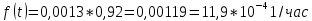 Ответ: 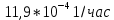 Задача 2.8 Невосстанавливаемая в процессе работы аппаратура состоит из 2000 элементов, средняя интенсивность отказов которых 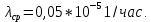 Время непрерывной работы аппаратуры t = 200 час. Определить вероятность безотказной работы и среднюю наработку до первого отказа. Время непрерывной работы аппаратуры t = 200 час. Определить вероятность безотказной работы и среднюю наработку до первого отказа.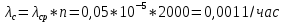 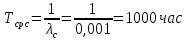 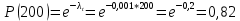 Ответ: 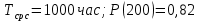 Задача 2.28 Изделие состоит из N элементов, средняя интенсивность отказов которых 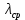 . Требуется вычислить вероятность безотказной работы в течение t и среднюю наработку до первого отказа. . Требуется вычислить вероятность безотказной работы в течение t и среднюю наработку до первого отказа.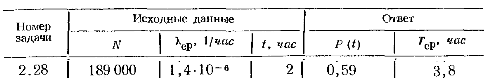 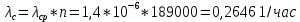 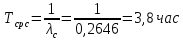 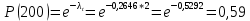 Ответ: 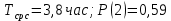 Задача 2.48 Изделие состоит из Nчастей. Надежность каждой части изделия характеризуется вероятностью 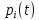 безотказной работы в течение времени t. Необходимо найти вероятность безотказной работы изделия. безотказной работы в течение времени t. Необходимо найти вероятность безотказной работы изделия.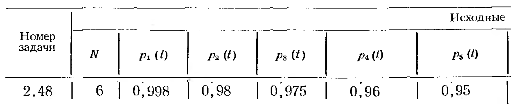 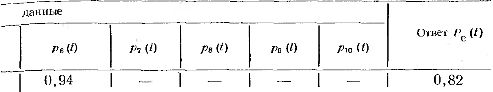 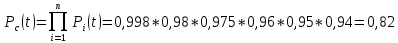 Задача 2.78 Изделие состоит из N групп приборов. Отказы первой группы подчинены экспоненциальному закону с интенсивностью отказов 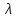 , отказы приборов второй группы — закону Релея с параметром σ и отказы приборов третьей группы — закону Вейбулла с параметрами , отказы приборов второй группы — закону Релея с параметром σ и отказы приборов третьей группы — закону Вейбулла с параметрами 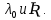 Необходимо найти вероятность безотказной работы в течение времени t. Необходимо найти вероятность безотказной работы в течение времени t. 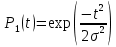 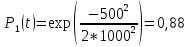 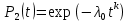 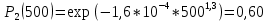 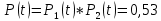 Ответ: 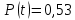 Задача 2.108 Система состоит из N элементов. Вероятность безотказной работы одного элемента в течение времени t равна 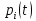 . Требуется определить вероятность безотказной работы системы. . Требуется определить вероятность безотказной работы системы. Вероятность безотказной работы системы найдем по формуле: 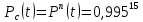 Вероятность 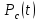 близка к единице, поэтому для ее вычисления воспользуемся формулой: близка к единице, поэтому для ее вычисления воспользуемся формулой: 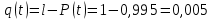 . .Тогда 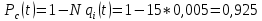 Ответ: 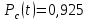 Задача 2.138 В изделии могут быть использованы только те элементы, средняя интенсивность отказов которых равна 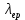 . Изделие имеет число элементов N. Требуется определить среднюю наработку до первого отказа и вероятность безотказной работы в конце первого часа. . Изделие имеет число элементов N. Требуется определить среднюю наработку до первого отказа и вероятность безотказной работы в конце первого часа. 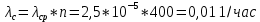 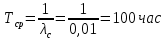 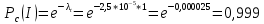 Ответ: 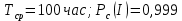 Задача 2.168 Необходимо выполнить ориентировочный расчет надежности системы, состоящей из N элементов различного типа. Требуется вычислить вероятность безотказной работы системы в течение времени t и среднюю наработку до первого отказа 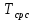 . .  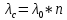 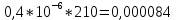 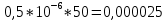 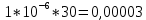 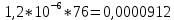 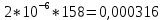 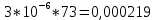 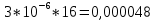 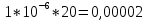 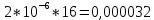 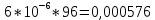 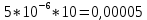 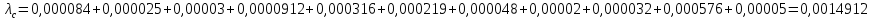 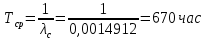 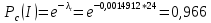 Ответ: 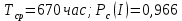 |
