Темы 1 - 11 - Контрольная работа. Задача Батарея, состоящая из 10 орудий, ведет огонь по 15 кораблям неприятеля. Найти вероятность того, что все орудия стреляют

• Название: Задача Батарея, состоящая из 10 орудий, ведет огонь по 15 кораблям неприятеля. Найти вероятность того, что все орудия стреляют
• Анкор: Темы 1 - 11 - Контрольная работа.doc
• Дата: 24.04.2017
• Размер: 114.5 Kb.
• Имя файла: Темы 1 - 11 - Контрольная работа.doc
• Тип: Задача; #3697

Контрольная работа. Темы 1 -12.

Вариант I

Задача 1. 12 студентов случайным образом рассаживаются на 12 первых местах одного ряда партера. Какова вероятность, что студенты М и Н будут сидеть рядом?
Задача 2. Батарея, состоящая из 10 орудий, ведет огонь по 15 кораблям неприятеля. Найти вероятность того, что все орудия стреляют:

а) по одной цели;

б) по разным целям (выбор цели случаен и не зависит от выбора других).
Задача 3. В ящике находится 20 лампочек, среди которых 3 перегоревшие. Найти вероятность того, что 10 лампочек, наудачу взятых из ящика, будут гореть.
Задача 4. На АТС могут поступать вызовы трех типов. Вероятности поступления вызовов первого, второго и третьего типа соответственно равны 0,2; 0,3; 0,5. Поступило три вызова. Какова вероятность того, что:

а) все они разных типов;

б) среди них нет вызова второго типа.
Задача 5. На елочный базар поступают елки из трех лесхозов, причем первый лесхоз поставил 50% елок, второй – 30% елок, а третий – 20%. Среди елок первого лесхоза 10% голубых, второго – 20%, а третьего – 30%. Куплена одна елка. Она оказалась голубой. Какова вероятность того, что она поставлена вторым лесхозом?
Задача 6. Вероятность того, что изделие не выдержит испытания, равна 0,004. Какова вероятность того, что из 750 проверяемых изделий более трех изделий не выдержат испытания?

_________________________________________________________________________________
Контрольная работа. Темы 1 -12.

Вариант II

Задача 1. 9 туристов наудачу рассаживаются по 12 вагонам электрички. Найти вероятность того, что все они окажутся

а) в одном вагоне?

б) во втором вагоне?

в) в разных вагонах?
Задача 2. В автопарке 20 экскурсионных автобусов двух марок 12 и 8 соответственно. Вероятность выезда на экскурсию автобусов каждой марки одна и та же. Какова вероятность того, что после выезда на экскурсию 16 автобусов, в автопарке остались автобусы: а) первой марки?

б) одной марки?

в) разных марок?
Задача 3. С вероятностью 0,4 посланное сообщение принимается при одной передаче. Сколько надо сделать передач, чтобы с вероятностью не менее 0,9 она была принята хотя бы один раз?
Задача 4. В одной коробке находятся 4 красных, 5 зеленых и 3 черных карандаша, а в другой коробке – 3 красных и 2 черных. Из первой коробки взяты три карандаша, из второй – два. Какова вероятность того, что все вытащенные карандаши одного цвета?
Задача 5. Из 1000 ламп 590 принадлежат первой партии, 200 – второй, а остальные – третьей. В первой партии %, во второй – 5%, в третьей – 4% бракованных ламп. Наудачу выбирается одна лампа. Какова вероятность того, что она бракованная?
Задача 6. Проведено 8 независимых испытаний, каждое из которых заключается в одновременном подбрасывании двух монет. Найти вероятность того, что:

а) в трех испытаниях из восьми появится по 2 Герба;

б) не менее двух раз выпадет 2 Герба.

Контрольная работа. Темы 1 -12.

Вариант III

Задача 1. В семизначном телефонном номере стерлись три последние цифры. Найти вероятность того, что стерлись:

а) одинаковые цифры;

б) разные цифры.
Задача 2. На устройство поступают два сигнала, причем поступление каждого сигнала в течение часа равновозможно. Устройство срабатывает, если разность между моментами поступления сигналов менее 10 минут. Найти вероятность того, что устройство сработает.
Задача 3. В урне находится 40 шаров. Вероятность того, что 2 извлеченных шара окажутся белыми, равна 7/60. Сколько в урне белых шаров.
Задача 4. Вероятность потери письма в почтовом отделении равна 0,03, а телеграммы – 0,01. Отправлено два письма и одна телеграмма. Какова вероятность того, что дойдет:

а) только телеграмма;

б) хотя бы одно из отправлений.
Задача 5. В пункте проката имеется 8 новых и 10 подержанных (т.е. хотя бы один раз использованных) автомобилей. Три машины взяли наугад в прокат и спустя некоторое время вернули. После этого вновь наудачу взяли в прокат два автомобиля. Какова вероятность того, что оба автомобиля новые?
Задача 6. Вероятность попадания в цель при каждом выстреле равна 0,8. Найти вероятность того, что при 5 выстрелах цель будет поражена:

а) два раза;

б) не менее двух раз;

в) не будет поражена ни разу.

________________________________________________________________________________________
Контрольная работа. Темы 1 -12.

Вариант IV

Задача 1. Два приятеля В и С решили, что за билетами в кино пойдет тот, у кого выпадет меньшее число очков при бросании игрального кубика. Какова вероятность того, что за билетами пойдет:

а) С;

б) проигравший;

в) выигравший.
Задача 2. В ящике 50 стандартных и 16 дефектных изделий. Сборщик наудачу достает 8 деталей. Найти вероятность того, что среди них:

а) нет дефектных;

б) 3 дефектных.
Задача 3. Вероятность того, что в результате пяти независимых опытов событие А произойдет хотя бы один раз равна 0,99757. Предполагается, что вероятность появления события А в каждом опыте одна и та же. Определить вероятность появления события А в одном опыте.
Задача 4. В мастерской три станка. Они требуют наладки в течение смены с вероятностями 0,05; 0,1 и 0,3 соответственно. Какова вероятность того, что в течение смены потребуется наладить:

а) все станки;

б) только один станок.
Задача 5. В первой урне 3 белых и 7 черных шаров, во второй – 5 белых и 2 черных. Из первой урны переложили во вторую три шара, затем из второй урны извлечен один шар. Какова вероятность того, что он белый?
Задача 6. По каналу связи передаются 7 сообщений, каждое из которых, независимо от других, может быть искажено с вероятностью 0,15. Найти вероятность того, что будет правильно принято не менее двух сообщений.
Контрольная работа. Темы 1 -12.

Вариант V

Задача 1. В ящике лежат девять кубиков с номерами от 1 до 9. Последовательно извлекаются три кубика. Найти вероятность того, что появятся кубики:

а) с номерами 2, 5 и 9;

б) с номерами 5, 2 и 9;

в) с номерами 4, 5, 4.
Задача 2. 52 игральные карты раздаются четверым игрокам. найти вероятность того, что:

а) все Тузы будут у одного игрока;

б) каждый игрок получит один Туз.
Задача 3. Три стрелка делают по одному выстрелу в цель. Вероятности попадания в цель соответственно равны 0,6; 0,85 и 0,7. Какова вероятность попадания в цель:

а) только второго стрелка?

б) хотя бы одного стрелка?
Задача 4. В мешке смешаны нити, среди которых 30% красных, 60% синих и остальные – белые. Какова вероятность того, что три наудачу вытянутые нити окажутся одного цвета?
Задача 5. На склад с оружием совершают налет четыре самолета. Вероятность поражения самолета системой ПВО равна 0,8. При прорыве k самолетов атакуемый объект будет уничтожен с вероятностью р_к. Найти вероятность уничтожения склада.
Задача 6. найти вероятность того, что в серии из 9 подбрасываний игрального кубика 5 очков выпадет менее трех раз.

_________________________________________________________________________________
Контрольная работа. Темы 1 -12.

Вариант VI

Задача 1. В круг вписан квадрат. Найти вероятность того, что случайная точка, брошенная в круг, не попадет в квадрат.
Задача 2. В цветочном ларьке продаются 8 аспарагусов и 5 гераний. Какова вероятность того, что среди 5 проданных растений:

а) 2 аспарагуса?

б) все герани?
Задача 3. В ящике 6 белых и 30 черных шаров. Какова вероятность того, что из двух вынутых шаров один белый, а другой черный?
Задача 4. Вероятность дозвониться с первой попытки в Справочное бюро вокзала составляет 0,4. Какова вероятность того, что:

а) удастся дозвониться при втором звонке?

б) придется звонить не более трех раз?
Задача 5. Батарея из трех орудий произвела залп, причем два снаряда попали в цель. Найти вероятность того, что третье орудие попало, если вероятности попадания в цель первым, вторым и третьим орудиями соответственно равны 0,5; 0,3 и 0,4.
Задача 6. Сообщение содержит 500 символов. Вероятность искажения символа при передаче постоянна и равна р. Если хотя бы один символ искажен, то сообщение принято неверно. При каких значениях р вероятность того, что сообщение будет успешно передано, окажется равной 0,95?

Контрольная работа. Темы 1 -12.

Ответы и решения
Вариант I

Задача 1. 12 студентов случайным образом рассаживаются на 12 первых местах одного ряда партера. Какова вероятность, что студенты М и Н будут сидеть рядом? Ответ:

Решение.
Задача 2. Батарея, состоящая из 10 орудий, ведет огонь по 15 кораблям неприятеля. Найти вероятность того, что все орудия стреляют:

а) по одной цели; Ответ:

Решение.

б) по разным целям (выбор цели случаен и не зависит от выбора других). Ответ:

Решение.
Задача 3. В ящике находится 20 лампочек, среди которых 3 перегоревшие. Найти вероятность того, что 10 лампочек, наудачу взятых из ящика, будут гореть. Ответ:

Решение.
Задача 4. На АТС могут поступать вызовы трех типов. Вероятности поступления вызовов первого, второго и третьего типа соответственно равны 0,2; 0,3; 0,5. Поступило три вызова. Какова вероятность того, что:

а) все они разных типов; Ответ:

Решение.

б) среди них нет вызова второго типа. Ответ:

Решение.
Задача 5. На елочный базар поступают елки из трех лесхозов, причем первый лесхоз поставил 50% елок, второй – 30% елок, а третий – 20%. Среди елок первого лесхоза 10% голубых, второго – 20%, а третьего – 30%. Куплена одна елка. Она оказалась голубой. Какова вероятность того, что она поставлена вторым лесхозом? Ответ:

Решение.
Задача 6. Вероятность того, что изделие не выдержит испытания, равна 0,004. Какова вероятность того, что из 750 проверяемых изделий более трех изделий не выдержат испытания? Ответ:

Решение.
Вариант II

Задача 1. 9 туристов наудачу рассаживаются по 12 вагонам электрички. Найти вероятность того, что все они окажутся

а) в одном вагоне? Ответ:

Решение.

б) во втором вагоне? Ответ:

Решение.

в) в разных вагонах? Ответ:

Решение.
Задача 2. В автопарке 20 экскурсионных автобусов двух марок 12 и 8 соответственно. Вероятность выезда на экскурсию автобусов каждой марки одна и та же. Какова вероятность того, что после выезда на экскурсию 16 автобусов, в автопарке остались автобусы: а) первой марки?

б) одной марки? Ответ:

Решение.

в) разных марок? Ответ:

Решение.
Задача 3. С вероятностью 0,4 посланное сообщение принимается при одной передаче. Сколько надо сделать передач, чтобы с вероятностью не менее 0,9 она была принята хотя бы один раз? Ответ:

Решение.
Задача 4. В одной коробке находятся 4 красных, 5 зеленых и 3 черных карандаша, а в другой коробке – 3 красных и 2 черных. Из первой коробки взяты три карандаша, из второй – два. Какова вероятность того, что все вытащенные карандаши одного цвета? Ответ:

Решение.
Задача 5. Из 1000 ламп 590 принадлежат первой партии, 200 – второй, а остальные – третьей. В первой партии %, во второй – 5%, в третьей – 4% бракованных ламп. Наудачу выбирается одна лампа. Какова вероятность того, что она бракованная? Ответ:

Решение.
Задача 6. Проведено 8 независимых испытаний, каждое из которых заключается в одновременном подбрасывании двух монет. Найти вероятность того, что:

а) в трех испытаниях из восьми появится по 2 Герба; Ответ:

Решение.

б) не менее двух раз выпадет 2 Герба. Ответ:

Решение.
Вариант III

Задача 1. В семизначном телефонном номере стерлись три последние цифры. Найти вероятность того, что стерлись:

а) одинаковые цифры; Ответ:

Решение.
б) разные цифры. Ответ:

Решение.
Задача 2. На устройство поступают два сигнала, причем поступление каждого сигнала в течение часа равновозможно. Устройство срабатывает, если разность между моментами поступления сигналов менее 10 минут. Найти вероятность того, что устройство сработает. Ответ:

Решение.
Задача 3. В урне находится 40 шаров. Вероятность того, что 2 извлеченных шара окажутся белыми, равна . Сколько в урне белых шаров. Ответ: .

Решение. Пусть m – количество белых шаров в урне. Тогда вероятность извлечения белого шара на первом шаге составляет , а на втором - . По правилу умножения: . Преобразуем: , откуда
Задача 4. Вероятность потери письма в почтовом отделении равна 0,03, а телеграммы – 0,01. Отправлено два письма и одна телеграмма. Какова вероятность того, что дойдет:

а) только телеграмма; Ответ:

Решение.

б) хотя бы одно из отправлений. Ответ:

Решение.
Задача 5. В пункте проката имеется 8 новых и 10 подержанных (т.е. хотя бы один раз использованных) автомобилей. Три машины взяли наугад в прокат и спустя некоторое время вернули. После этого вновь наудачу взяли в прокат два автомобиля. Какова вероятность того, что оба автомобиля новые? Ответ:

Решение.
Задача 6. Вероятность попадания в цель при каждом выстреле равна 0,8. Найти вероятность того, что при 5 выстрелах цель будет поражена:

а) два раза; Ответ: 0,0512;

Решение. По формуле Бернулли .

б) не менее двух раз; Ответ:

Решение.

в) не будет поражена ни разу. Ответ: 0,00032.

Решение. По формуле Бернулли .
Вариант IV

Задача 1. Два приятеля В и С решили, что за билетами в кино пойдет тот, у кого выпадет меньшее число очков при бросании игрального кубика. Какова вероятность того, что за билетами пойдет:

а) С; Ответ:

Решение.

б) проигравший; Ответ:

Решение.

в) выигравший. Ответ:

Решение.
Задача 2. В ящике 50 стандартных и 16 дефектных изделий. Сборщик наудачу достает 8 деталей. Найти вероятность того, что среди них:

а) нет дефектных; Ответ:

Решение. Стандартных изделий в партии – 50-16 = 34, следовательно, .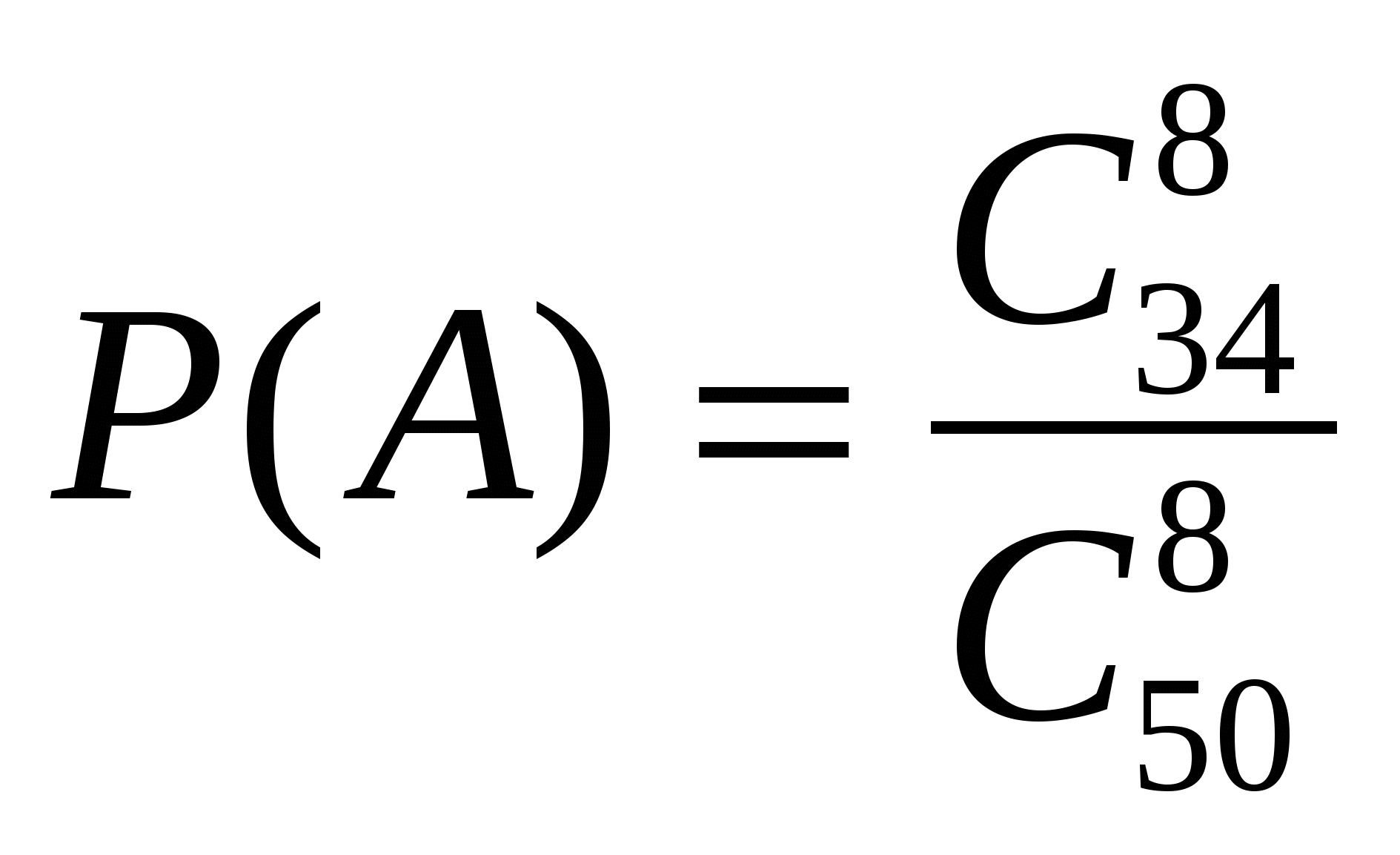

б) 3 дефектных. Ответ:

Решение.
Задача 3. Вероятность того, что в результате пяти независимых опытов событие А произойдет хотя бы один раз равна 0,99757. Предполагается, что вероятность появления события А в каждом опыте одна и та же. Определить вероятность появления события А в одном опыте. Ответ: .

Решение. По условию . Введем противоположное событие В = {в серии опытов событие А не произошло ни разу}. . Отсюда 0,00243, ; .
Задача 4. В мастерской три станка. Они требуют наладки в течение смены с вероятностями 0,05; 0,1 и 0,3 соответственно. Какова вероятность того, что в течение смены потребуется наладить:

а) все станки; Ответ:

Решение.

б) только один станок. Ответ:

Решение.
Задача 5. В первой урне 3 белых и 7 черных шаров, во второй – 5 белых и 2 черных. Из первой урны переложили во вторую три шара, затем из второй урны извлечен один шар. Какова вероятность того, что он белый? Ответ:

Решение.
Задача 6. По каналу связи передаются 7 сообщений, каждое из которых, независимо от других, может быть искажено с вероятностью 0,15. Найти вероятность того, что будет правильно принято не менее двух сообщений. Ответ:

Решение.
Вариант V

Задача 1. В ящике лежат девять кубиков с номерами от 1 до 9. Последовательно извлекаются три кубика. Найти вероятность того, что появятся кубики:

а) с номерами 2, 5 и 9; Ответ:

Решение.

б) с номерами 5, 2 и 9; Ответ:

Решение.

в) с номерами 4, 5, 4. Ответ:

Решение.
Задача 2. 52 игральные карты раздаются четверым игрокам. Найти вероятность того, что:

а) все Тузы будут у одного игрока; Ответ:

Решение.

б) каждый игрок получит один Туз. Ответ:

Решение.
Задача 3. Три стрелка делают по одному выстрелу в цель. Вероятности попадания в цель соответственно равны 0,6; 0,85 и 0,7. Какова вероятность попадания в цель:

а) только второго стрелка? Ответ:

Решение.

б) хотя бы одного стрелка? Ответ:

Решение.
Задача 4. В мешке смешаны нити, среди которых 30% красных, 60% синих и остальные – белые. Какова вероятность того, что три наудачу вытянутые нити окажутся одного цвета? Ответ: .

Решение. .
Задача 5. На склад с оружием совершают налет четыре самолета. Вероятность поражения самолета системой ПВО равна 0,8. При прорыве k самолетов атакуемый объект будет уничтожен с вероятностью р_к. Найти вероятность уничтожения склада. Ответ:

Решение.
Задача 6. Найти вероятность того, что в серии из 9 подбрасываний игрального кубика 5 очков выпадет менее трех раз. Ответ:

Решение. По формуле Бернулли
Вариант VI

Задача 1. В круг вписан квадрат. Найти вероятность того, что случайная точка, брошенная в круг, не попадет в квадрат. Ответ: .

Решение. Пусть R – радиус круга, тогда длина стороны квадрата - . Искомая вероятность .
Задача 2. В цветочном ларьке продаются 8 аспарагусов и 5 гераний. Какова вероятность того, что среди 5 проданных растений:

а) 2 аспарагуса? Ответ:

Решение.

б) все герани? Ответ:

Решение.
Задача 3. В ящике 6 белых и 30 черных шаров. Какова вероятность того, что из двух вынутых шаров один белый, а другой черный? Ответ:

Решение.
Задача 4. Вероятность дозвониться с первой попытки в Справочное бюро вокзала составляет 0,4. Какова вероятность того, что:

а) удастся дозвониться при втором звонке? Ответ:

Решение.

б) придется звонить не более трех раз? Ответ:

Решение.
Задача 5. Батарея из трех орудий произвела залп, причем два снаряда попали в цель. Найти вероятность того, что третье орудие попало, если вероятности попадания в цель первым, вторым и третьим орудиями соответственно равны 0,5; 0,3 и 0,4. Ответ:

Решение.
Задача 6. Сообщение содержит 500 символов. Вероятность искажения символа при передаче постоянна и равна р. Если хотя бы один символ искажен, то сообщение принято неверно. При каких значениях р вероятность того, что сообщение будет успешно передано, окажется равной 0,95? Ответ:

Решение.