Задачи по графам.. Задачи_окончательный. Задача. Дан орграф порядка 6 Сколько в нем маршрутов длины 3 Записать их. Решение
 Скачать 227.73 Kb. Скачать 227.73 Kb.
|
|
6 вариант Маршруты в орграфе Задача. Дан орграф порядка 6 Сколько в нем маршрутов длины 3? Записать их. 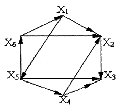 Решение. Используем алгебраический метод решения задачи. Запишем матрицу смежности. Матрица смежности орграфа - несимметричная:  Возведем эту матрицу в степень3: 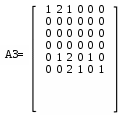 Суммируя все элементы полученной матрицы, находим, что число маршрутов длиной 3 равно двенадцати. Три единицы, стоящие по диагонали, показывают, что сюда входит 3 помеченных контура. Очевидно, это контуры X1–X5–X6, X5–X6–X1 и X6–X1–X5. 2. Компоненты сильной связности графа Задача. Найти компоненты сильной связности орграфа 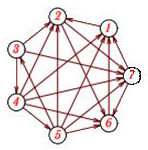 Решение. Найдем матрицу смежности вершин орграфа G:  Найдем матрицу достижимости вершин орграфа: 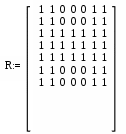 Найдем матрицу контрдостижимости вершин орграфа: 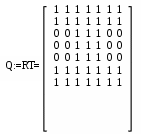 Отсюда получаем матрицу сильных компонент связности орграфа:  Таким образом, данный орграф содержит сильные компоненты связности G1 = (1,2,6,7). 3. Кратчайший путь в орграфе Задача. Для заданного орграфа найти кратчайший путь от вершины s к вершине t. На рисунке рядом с дугой указан ее вес. 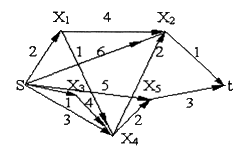 Решение. 1. Вершина s получает постоянную метку 0, остальные - метку ∞: 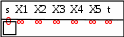 2. Вычисляем расстояния от вершины s с постоянной меткой 0. Вершины X1, X2, X3, X4 и X5 меняют свои временные метки на 2, 6, 1, 3 и 5. Вершина t имеет прежнюю метку - ∞. Очевидно, наименьшей меткой является 1. Она и становится постоянной:  3. Вычисляем расстояния от вершины X3 с постоянной меткой 1. Вершина X4 имеет расстояния 4 до вершины X3. Суммируя, получаем значение 5. Для вершины X4 прежнее значение 3, было меньше нового значения 5. Следовательно, значение метки X4 не меняем; оно остается равным 3. Вершины X1, X2, X5 не имеют соединения с вершиной X3, поэтому просто переносим их значения на новую строку. Из трех временных меток — 2, 6 3 и 5 - наименьшая принадлежит вершине X1. Эта метка и становится постоянной:  4. Вычисляем расстояния от вершины X1 с постоянной меткой 2. Вершина X4 имеет до нее расстояние 1. Суммируя (1+2), получаем значение 3 временной метки вершины X4, равное прежнему значению. Вершина X2 имеет расстояние 4 до вершины X1. Суммируя (2+4), получаем значение 6 временной метки вершины X2, равное предыдущему значению. Вершина X5 не имеет соединения с вершиной X1, поэтому просто переписываем значение 5 на новую строку. Из трех временных меток вершин 6, 3 и 5 наименьшая принадлежит вершине X4. Эта метка и становится постоянной: 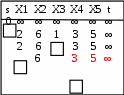 5. На следующем этапе, вычисляя расстояния от вершины X4 с постоянной меткой 3. Вершины X2 и X5, имеют расстояние до X4 2 и 2, соответственно. Суммируя с значением метки X4 (2+3), у обеих вершин получаем расстояние, равное 5. При одинаковых значениях вершин X2 и X5, суммируем значения их меток с расстоянием до вершины t. От X5 до t, расстояние (5+3) равно 8, а от вершины X2 (5+1) равно 6. Соответственно метка вершины X6 становится постоянной. А минимальное расстояние между вершинами s и t равно 6. 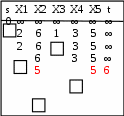 4. Поток в сети Задача. Задана пропускная способность дуг транспортной сети с началом (истоком) в вершине S и концом (стоком) в вершине t. Используя алгоритм Форда – Фалкерсона, найти максимальный поток по сети. 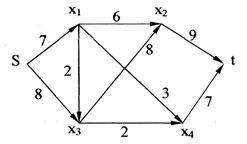 Решение. Алгоритм состоит из двух частей — насыщения потока и его перераспределения. 1. Насыщение потока. Рассмотрим путь S–X1–X2–t. Пропустим через этот путь поток, равный 6. При этом дуга [X1, X2] будет насыщенной. Аналогично, путь S–X3–X4–t - насытим потоком 2, дуга [X3, X4] будет насыщенной. Распределение потока отметим на графе. В числителе ставим пропускную способность, в знаменателе — поток. Числитель всегда больше знаменателя, а знаменатель может быть и нулем. 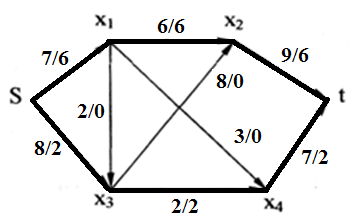 Заметим, что из S в t есть еще 2 ненасыщенных пути. Первый путь S–X1–X4–t, поток в котором можно увеличить на 1. При этом насытится дуга [S, X1]. 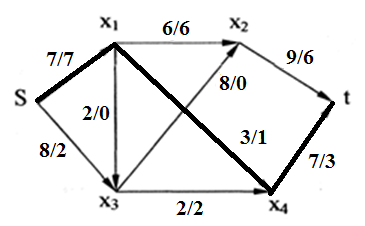 Второй путь S–X3–X2–t, поток в котором можно увеличить на 3. При этом насытится дуга [X2, t]. 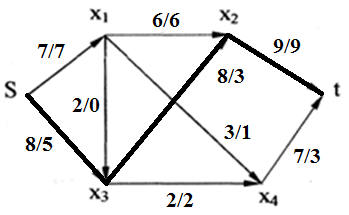 Из S в t больше нет ненасыщенных путей. По дуге [S, X1] двигаться нельзя (она уже насыщена), а движение по дуге [S, X3] проходит через дуги [X3, X2] и [X2, t] – эта дуга также насыщена. 2. Перераспределение потока. Найдем последовательность вершин от S к t, такую, что дуги, соединяющие соседние вершины, направленные из S в t, не насыщены, а дуги, направленные в обратном направлении, не пусты. В единственной последовательности: S–X3–X1–X4–t дуга [X3, X1] в обратном направлении пуста. Перераспределение потока не выполняется. На рисунке указаны потоки. 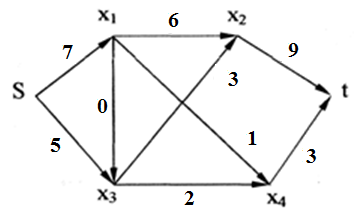 Поток в насыщенной сети можно посчитать по потоку, выходящему из истока S или входящему в сток t. Очевидно, эти числа должны быть равны. Кроме того, для проверки решения следует проверить условие сохранения потока по узлам. Для каждого узла суммарный входящий поток должен быть равен выходящему. Максимальный поток от вершины S к вершине t равен 12. |
