Олимпиадные задания. 5 кл 21-22. Задача Денис расставил числа от 1 до 9 в клетки квадрата 33 так, что сумма чисел во всех строках и во всех столбцах равна 15. А лёша стёр числа от 1 до 5 и вместо них написал буквы , , , и .
 Скачать 68.48 Kb. Скачать 68.48 Kb.
|
|
Внутришкольная олимпиада 2021-2022 учебного года Математика 5 классЗадача 5.1. Денис расставил числа от 1 до 9 в клетки квадрата 3×3 так, что сумма чисел во всех строках и во всех столбцах равна 15. А Лёша стёр числа от 1 до 5 и вместо них написал буквы 𝐴, 𝐵, 𝐶, 𝐷 и 𝐸. Получившийся квадрат изображён на рисунке. 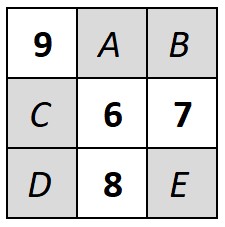 Где какие числа стояли первоначально?
Задача 5.2. Из квадрата со стороной 10 вырезали зелёный квадрат со стороной 2, синий квадрат и жёлтый прямоугольник (см. рисунок). Чему равен периметр оставшейся фигуры? Периметр фигуры — сумма длин всех её сторон. 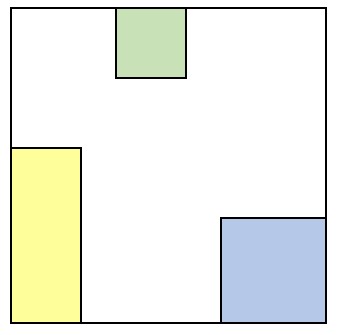 Задача 5.3. Ирина плохо учила математику в начале учебного года, поэтому в журнале у неё стояло 3 тройки и 2 двойки. Но в середине октября она собралась с силами и начала получать только пятёрки. Какое минимальное количество пятёрок нужно получить Ирине, чтобы её средний балл стал в точности равен 4? Задача 5.4. Алёна, Боря, Вера и Полина собирали яблоки в саду. Кто-то из них собрал 11 яблок, другой — 17, третий — 19, четвёртый — 24. Известно, что одна из девочек собрала 11 яблок; Алёна собрала яблок больше, чем Боря; суммарное количество яблок, собранное Алёной и Верой, делится на 3. Кто сколько яблок собрал?
Задача 5.5. Квадрат 2×2 можно разрезать на маленький квадратик и уголок четырьмя способами. Все способы разрезания показаны на рисунке ниже. Сколько существует способов разрезать квадрат 4×4 на три уголка и маленький квадратик, изображённые на рисунке? (Способы, отличающиеся поворотом или переворотом квадрата, считаются различными.) 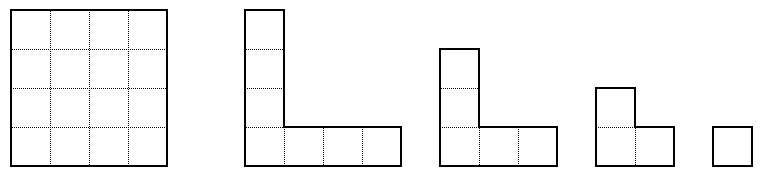  |
