6872200_Задача 4. Задача Динамика валового сбора сельскохозяйственных культур в хозяйстве характеризуется следующими данными

• Название: Задача Динамика валового сбора сельскохозяйственных культур в хозяйстве характеризуется следующими данными
• Дата: 24.03.2022
• Размер: 20.67 Kb.
• Имя файла: 6872200_Задача 4.docx
• Тип: Задача; #413895

Задача 4.

Динамика валового сбора сельскохозяйственных культур в хозяйстве характеризуется следующими данными:

Год	Темы прироста валового сбора по сравнению с предыдущим годом, в %
	Озимая пшеница	Сахарная свекла	Подсолнечник
2008	+20	-10	+5
2009	-5	+14	+11
2010	+7	+9	-7
2011	+2	-15	+14
2012	+14	+10	+5

1. 
   Определите валовой сбор культуры в 2012 г. по сравнению с 2007 г. увеличился в наибольшей степени, какой – в наименьшей степени.
   
2. 
   Рассчитайте, на сколько центнеров повысился валовой сбор каждой культуры за рассматриваемый период, если известно, что в 2007 г. Собрано: озимой пшеницы – 40 тыс.ц., сахарной свеклы – 30 тыс. ц., подсолнечника – 1600 ц.
   

Решение.

1. 
   На основе цепных темпов прироста из формулы
   рассчитаем цепные темпы роста:
   

Озимая пшеница 2008г. Т_р(ц)=(+20+100)/100=1,2

2009г. Т_р(ц)=(-5+100)/100=0,95

2010г. Т_р(ц)=(+7+100)/100=1,07

2011г. Т_р(ц)=(+2+100)/100=1,02

2012г. Т_р(ц)=(+14+100)/100=1,14

Сахарная свекла 2008г. Т_р(ц)=(-10+100)/100=0,9

2009г. Т_р(ц)= ₎=(+14+100)/100=1,14

2010г. Т_р(ц)=(+9+100)/100=1,09

2011г. Т_р(ц)=(-15+100)/100=0,85

2012г. Т_р(ц)=(+10+100)/100=1,1

Подсолнечник 2008г. Т_р(ц)=(+5+100)/100=1,05

2009г. Т_р(ц)= ₎=(+11+100)/100=1,11

2010г. Т_р(ц)=(-7+100)/100=0,93

2011г. Т_р(ц)=(+14+100)/100=1,14

2012г. Т_р(ц)=(+5+100)/100=1,05

На основе цепных темпов роста определим базисный темп роста 2012 года в сравнении с базисным годом (2007г), так как произведение цепных коэффициентов роста равно базисному:

Озимая пшеница 1,2*0,95*1,07*1,02*1,14=1,42

Сахарная свекла 0,9*1,14*1,09*0,85*1,1=1,05

Подсолнечник 1,05*1,11*0,93*1,14*1,05=1,3

Соответственно базисный темп прироста составляет:

Озимая пшеница (1,42-1)*100=42%

Сахарная свекла (1,05-1)*100=5%

Подсолнечник (1,3-1)*100=30%

Из базисных темпов прироста можем сделать вывод о том, что в наибольшей степени увеличился валовой сбор озимой пшеницы (на 42%), в наименьшей степени – валовой сбор сахарной свеклы (на 5%).

2. 
   Валовой сбор каждой культуры за рассматриваемый период увеличился:
   

Озимой пшеницы на 16800 центнеров ((40000ц. * 42%)/100%)

Сахарной свеклы на 1500 центнеров ((3000*5%)/100%)

Подсолнечника на 480 центнеров ((1600*30%)/100%)

Задача 14.

В таблице приведены данные об остатках оборотных средств торговой фирмы на начало месяца:

Дата	1 января	1 февраля	1 марта	1 апреля
Остатки оборотных средств, млн.руб.	21,5	22,7	24,3	23,8

Рассчитайте средние остатки оборотных средств за квартал.

Решение.

Средние остатки за квартал рассчитаем по формуле средней хронологической для моментного ряда с равноотстоящими уровнями:



где - значение признака в i-ый момент времени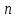

– количество значений



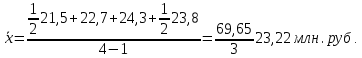Задача 15.

В таблице приведены данные об остатках готовой продукции на складе за год по состоянию на отдельные даты:

Дата	1 января	1 апреля	1 августа	1 октября	1 декабря
Остатки готовой продукции, млн.руб.	3,7	4,1	3,5	3,9	3,2

Рассчитайте среднегодовую стоимость остатков готовой продукции на складе предприятия.

Решение.

Если интервальный ряд имеет неравноотстоящие уровни, то средний уровень ряда вычисляется по формуле средней арифметической взвешенной: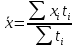



где - значение признака в i-ый момент времени;

- длительность интервала времени между уровнями.

Если в качестве длительности интервала возьмем месяцы:



Если в качестве длительности интервала возьмем дни: