|
|
Задача для движения 1 чцы в заданном внешнем поле. Для решения уря надо знать и
1.1.Разделение переменных.
m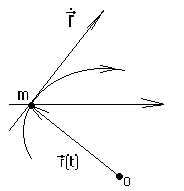 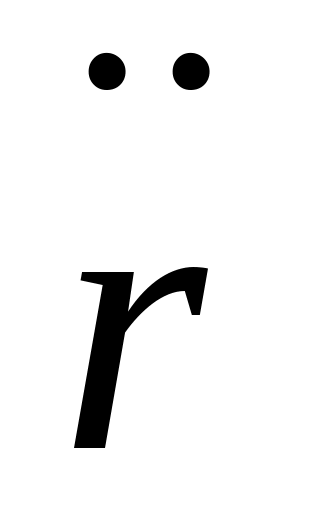 (t)= (t)=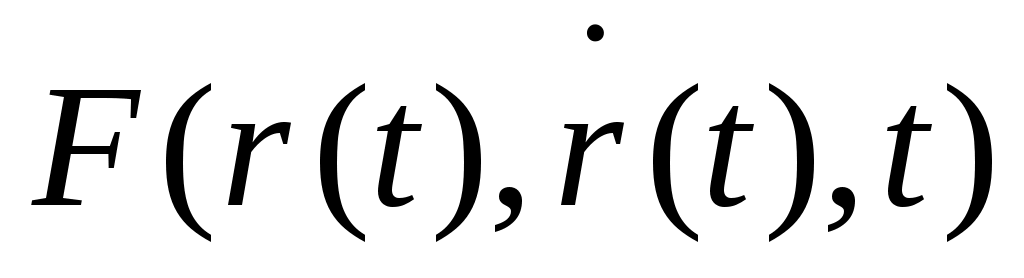 — (1) — ур-е дв-я. — (1) — ур-е дв-я.
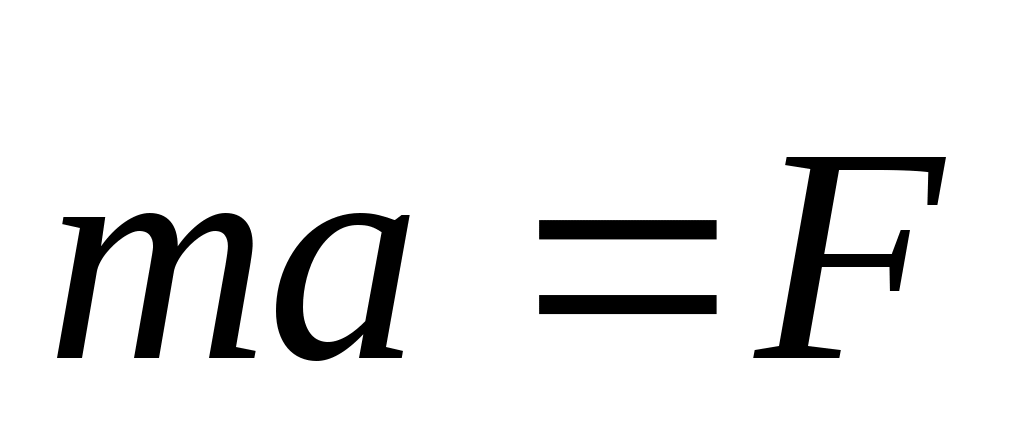 — определение силы. — определение силы. 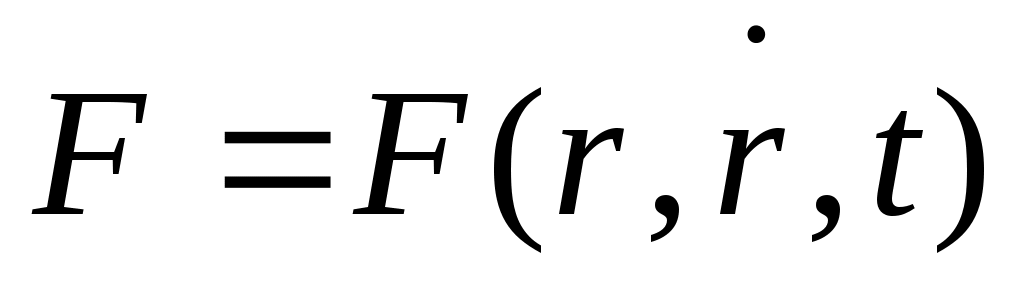
(1) – диф. ур. II порядка отн-но 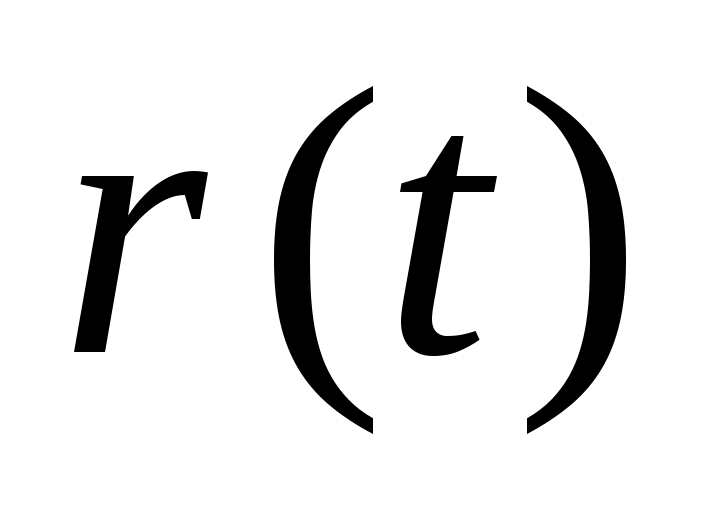 . Задаем нач. коорд. . Задаем нач. коорд. 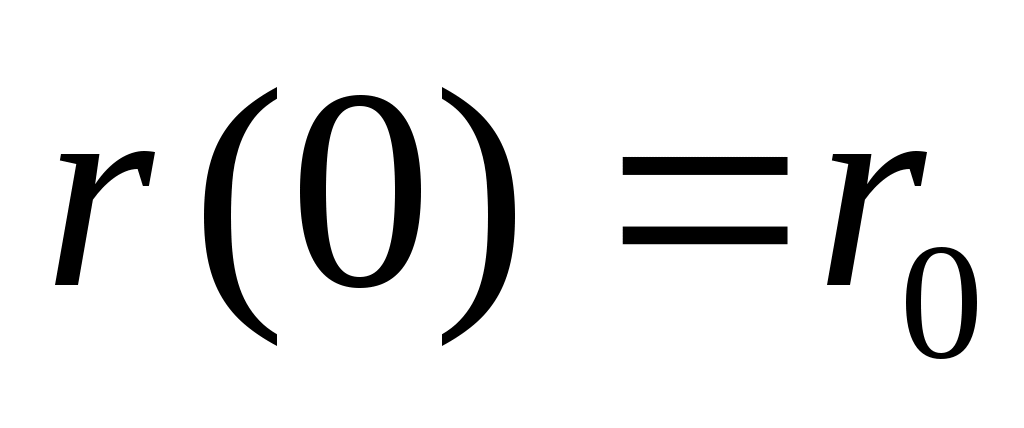 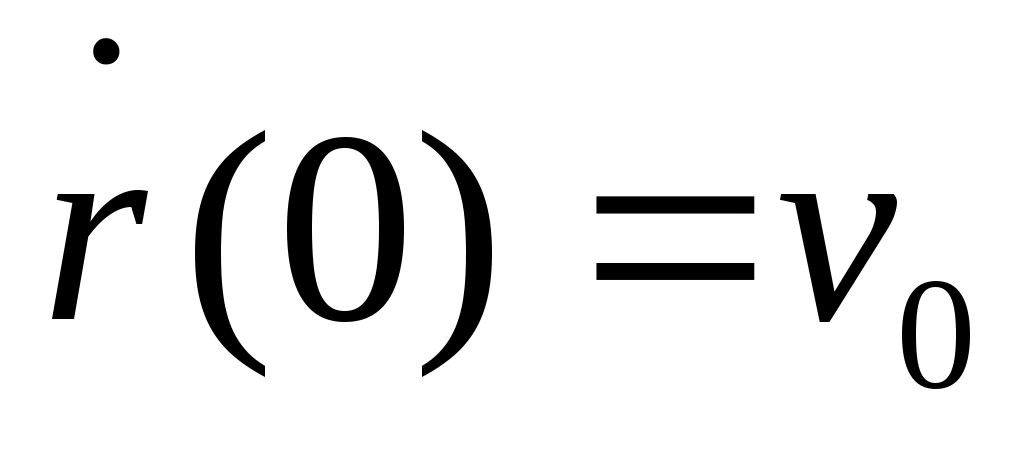 . Так формируется задача для движения 1 ч-цы в заданном внешнем поле. Для решения ур-я надо знать __ и …. . . Так формируется задача для движения 1 ч-цы в заданном внешнем поле. Для решения ур-я надо знать __ и …. .
Н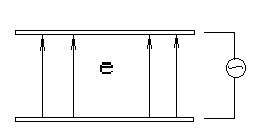 о (1) — это не 1 ур. а 3: о (1) — это не 1 ур. а 3:
 ; ; ; ;
 — это и есть разделение переменных. Вместо того, чтобы рассматривать движение точки в трехмерном пространстве, рассмотрим решение трех одномерных движений. — это и есть разделение переменных. Вместо того, чтобы рассматривать движение точки в трехмерном пространстве, рассмотрим решение трех одномерных движений.
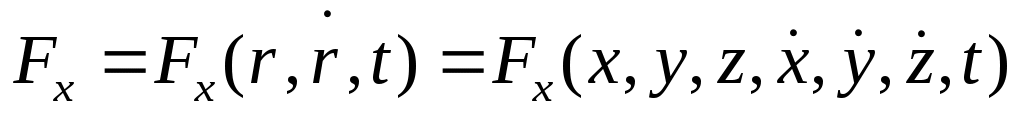 В частном случае может оказаться так, что В частном случае может оказаться так, что 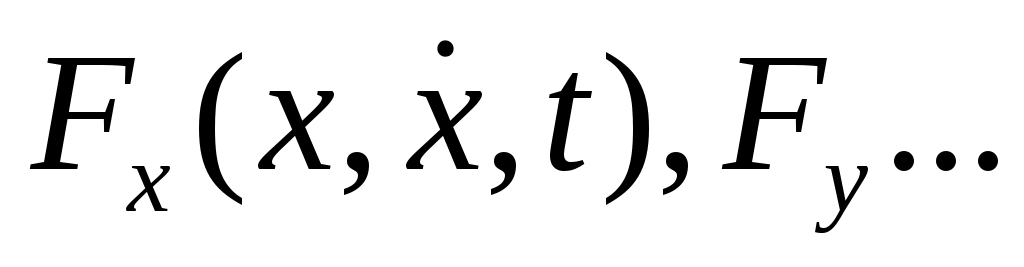 — это уравнение — это уравнение 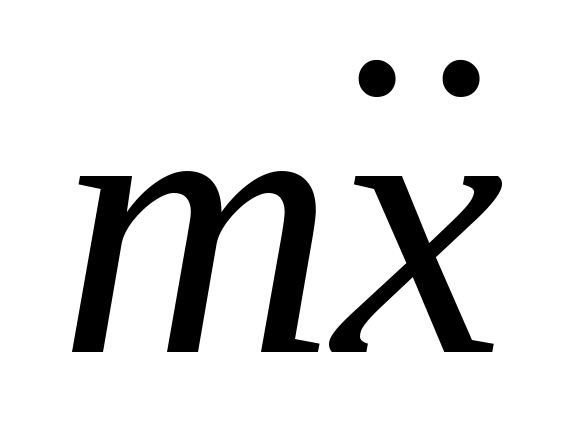 можно решать отдельно от других уравнений: можно решать отдельно от других уравнений:  — проекция точки, — проекция точки, 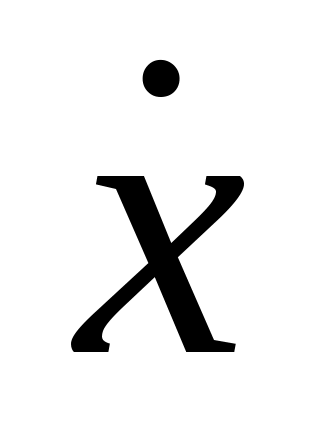 — проекция скорости движения только вдоль оси — проекция скорости движения только вдоль оси  . Такое движение называется одномерным. . Такое движение называется одномерным.
1.2. Одномерное движение под действием силы F(t).
Рассматривая двух- и трехмерное движение 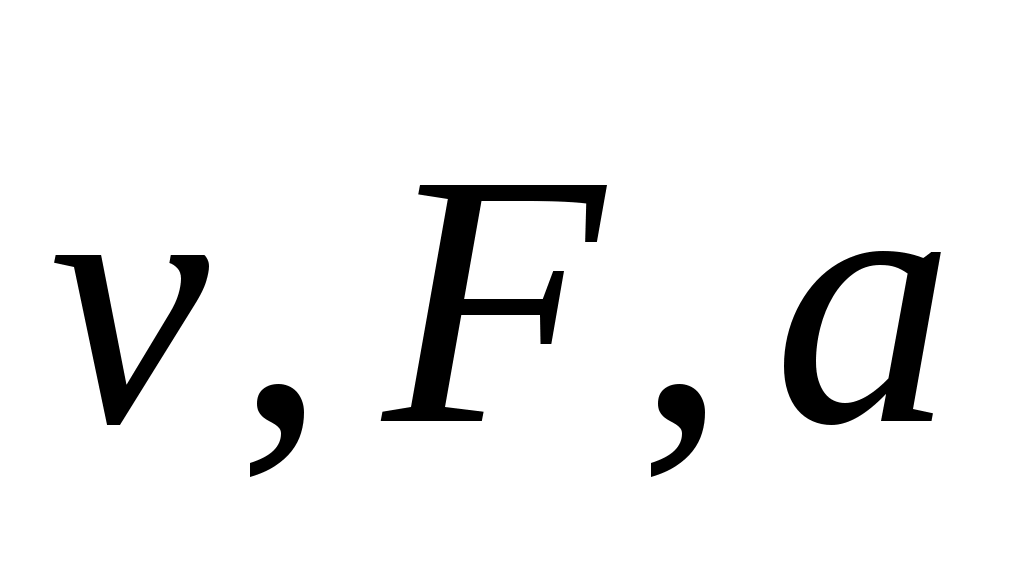 обозначают вектора скорости, силы и ускорения. Абс. величину этих векторов обозначаем обозначают вектора скорости, силы и ускорения. Абс. величину этих векторов обозначаем  , то они не могут быть ни “—“ ни “+”, а их проекции , то они не могут быть ни “—“ ни “+”, а их проекции 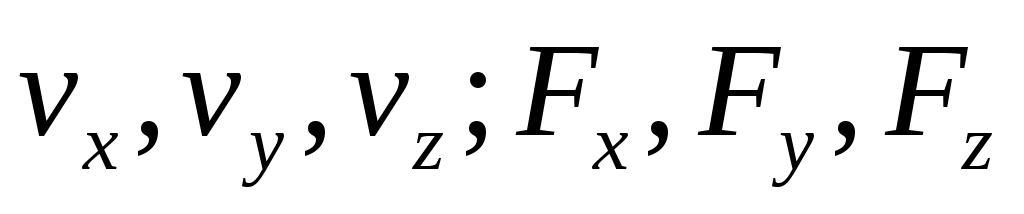 — могут. Но в одномерных задачах индекс опускается, т.к. не рассматриваются другие проекции. В одномерных — — могут. Но в одномерных задачах индекс опускается, т.к. не рассматриваются другие проекции. В одномерных —  - проекции, а в многомерных - проекции, а в многомерных  - абс. величины. - абс. величины.
Рассм. конденсатор.
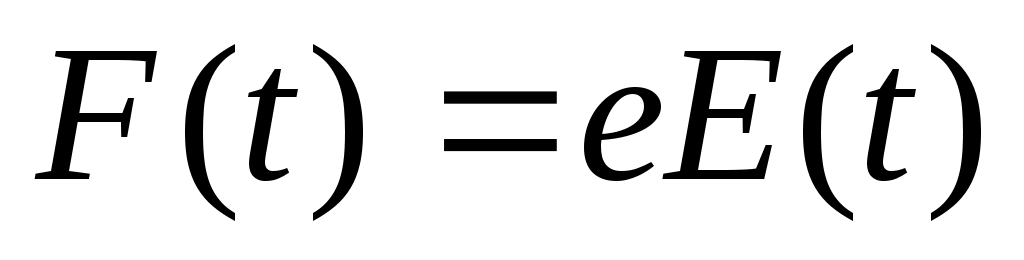 . В одном. . В одном.
случае получ. ДУ 2 пор.  с пост. коэф-ом m. с пост. коэф-ом m.  ; ;   ; ;  ; ;  ; ;  ; ; 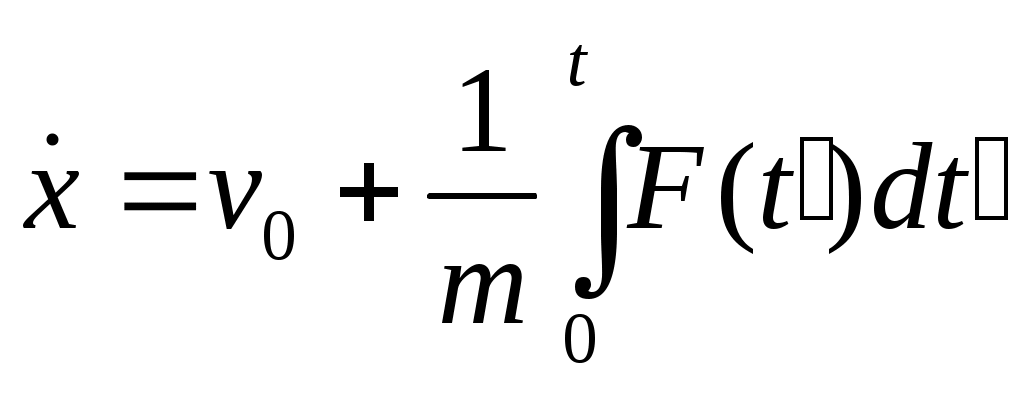 — результат 1-го интегрирования Ур-я Ньютона в этой задаче. Интегрируем еще раз. — результат 1-го интегрирования Ур-я Ньютона в этой задаче. Интегрируем еще раз.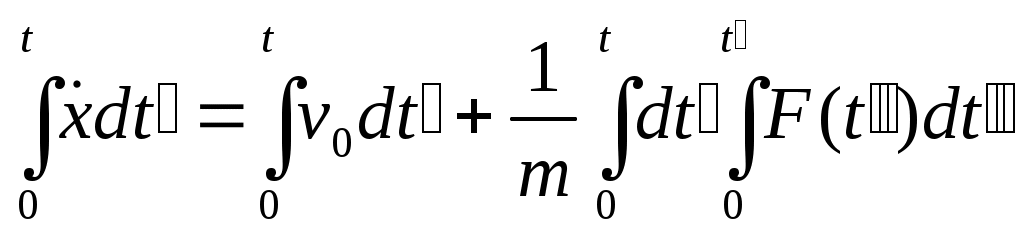 ; ; 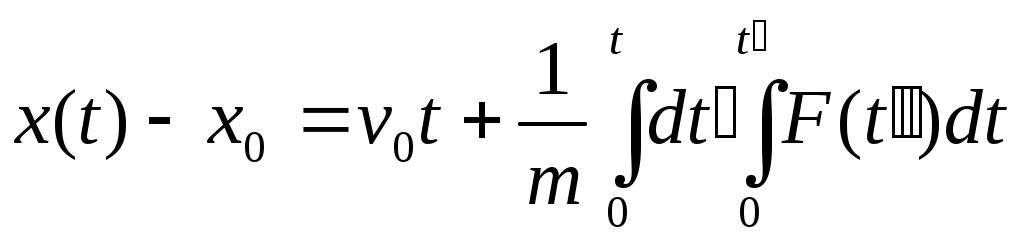 ; ; 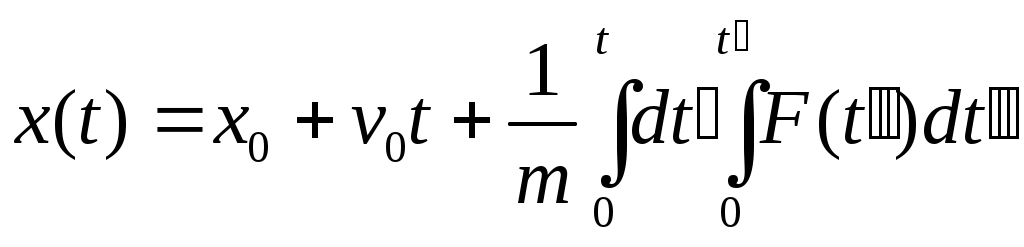 (*) Предположим, что F не зависит от времени, тогда преобразуем в одинарный интеграл. Применим правило Дирихле: Если бы пределы интегрирования были постоянными, то можно поменять местами. Но здесь 1 из пределов является переменной величиной, тогда переходим к дополнительной области интегрирования от t′′ до t: (*) Предположим, что F не зависит от времени, тогда преобразуем в одинарный интеграл. Применим правило Дирихле: Если бы пределы интегрирования были постоянными, то можно поменять местами. Но здесь 1 из пределов является переменной величиной, тогда переходим к дополнительной области интегрирования от t′′ до t: 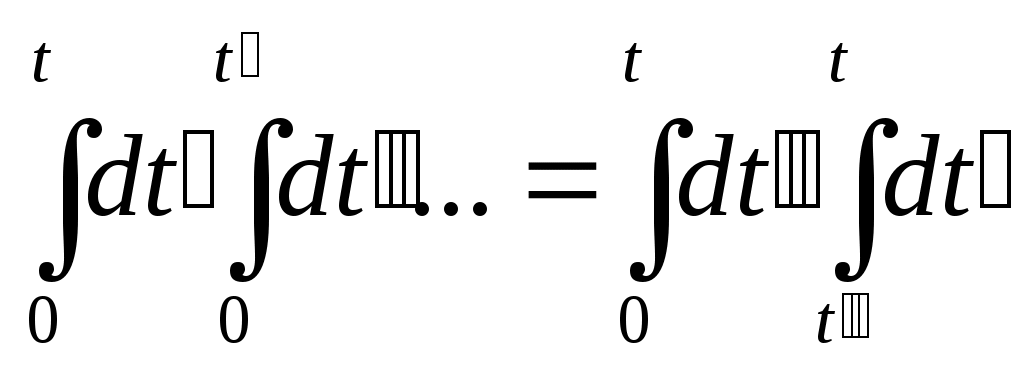 — правило Дирихле. Применяя его к (*), получим: — правило Дирихле. Применяя его к (*), получим: 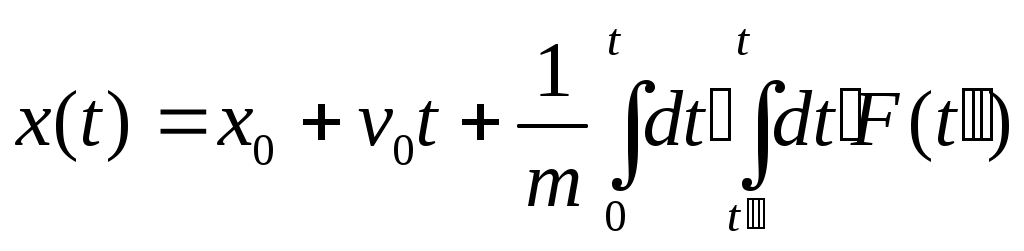 ; ; 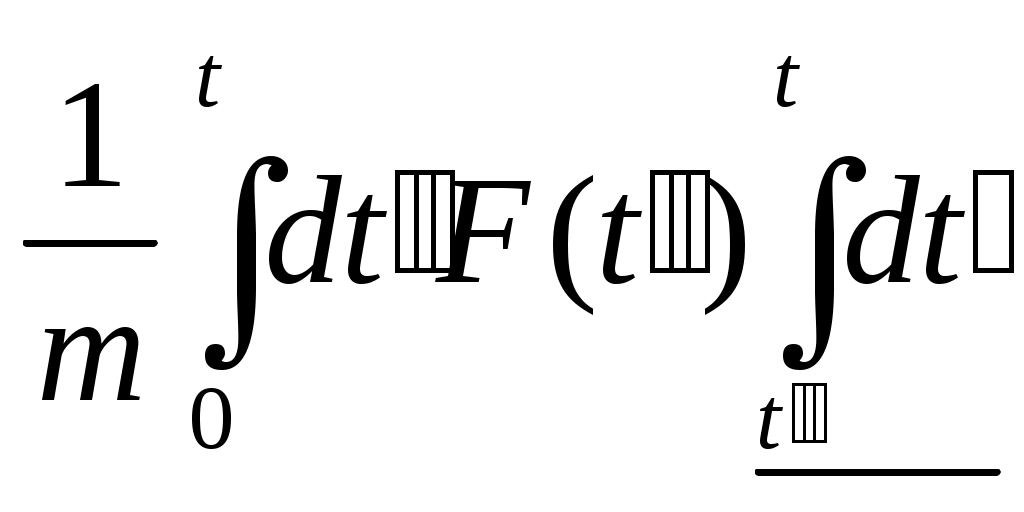 Сосчитаем внутр. Интеграл, тогда получим: t- t′′ Сосчитаем внутр. Интеграл, тогда получим: t- t′′
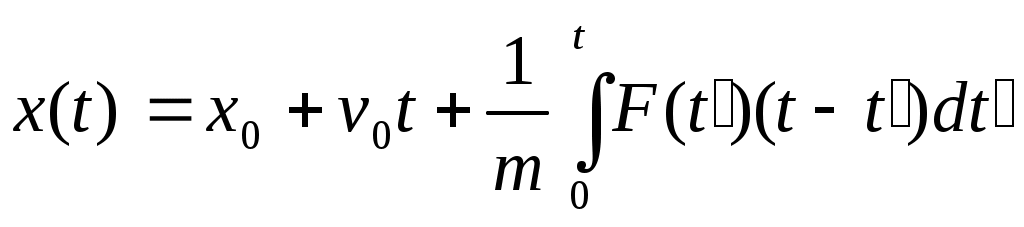 (замена двойного штриха одинарным). (замена двойного штриха одинарным).
1.3. Одномерное движение под д-ем силы F(v).
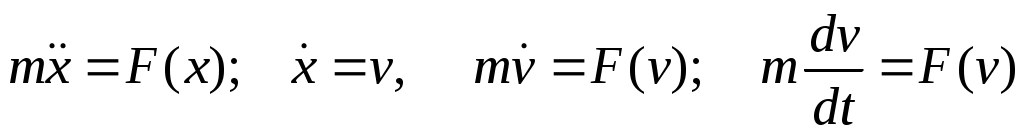 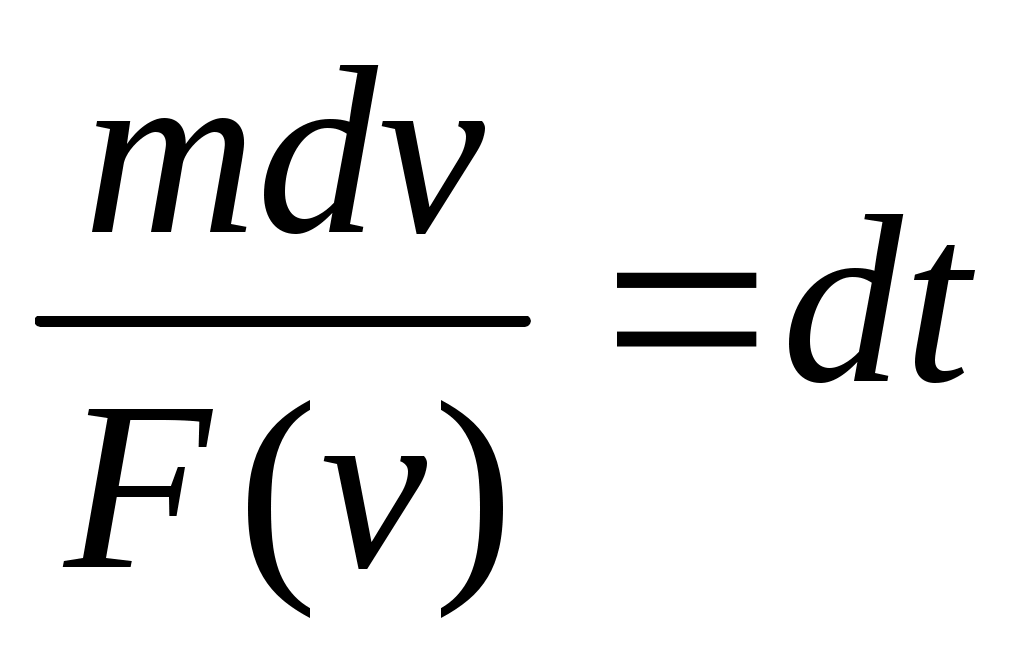 Разделили переменные. Интегрируем: Разделили переменные. Интегрируем: 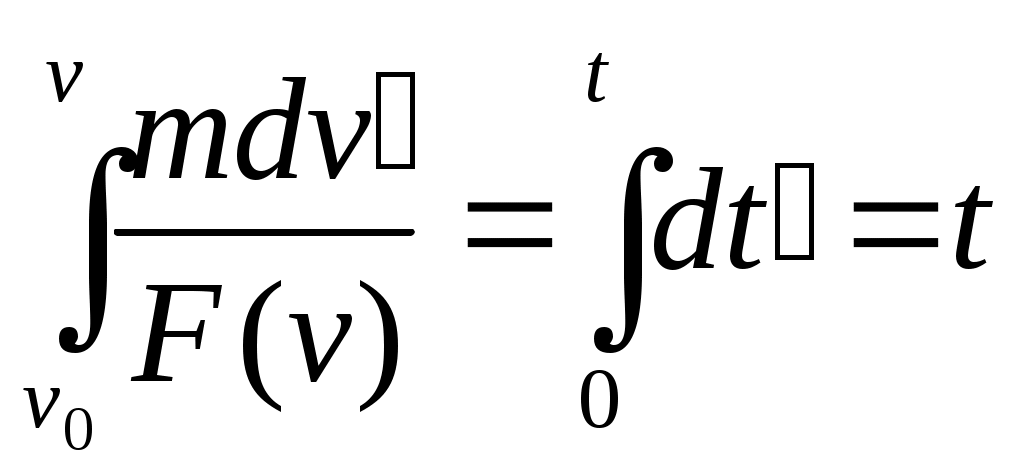 Получаем решение в виде: Получаем решение в виде: 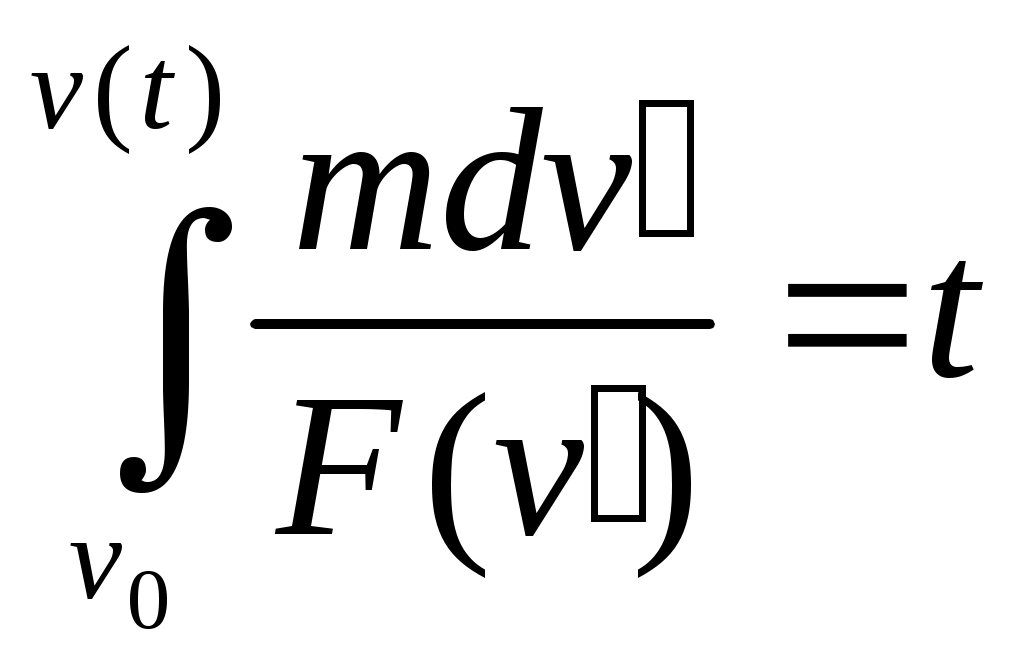 здесь t=f(v) — некот. ф-я от верхнего предела. А надо найти v как ф-ю от t. Это делается переходом к обр. ф-ии v = f-1(t). v=dx/dt. dx/dt=f-1(t) здесь t=f(v) — некот. ф-я от верхнего предела. А надо найти v как ф-ю от t. Это делается переходом к обр. ф-ии v = f-1(t). v=dx/dt. dx/dt=f-1(t)
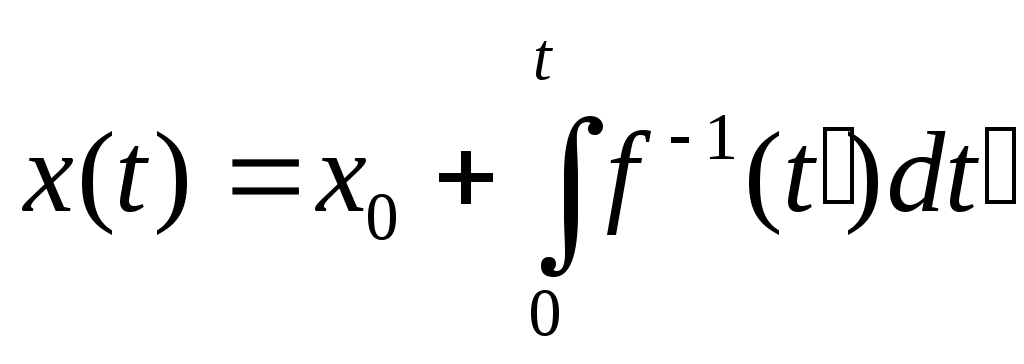 Для существования ф-ии надо, чтобы t=f(v) была монотонной. Для существования ф-ии надо, чтобы t=f(v) была монотонной.
1.4 Движение частицы в поле, зависящем от координат F(x).
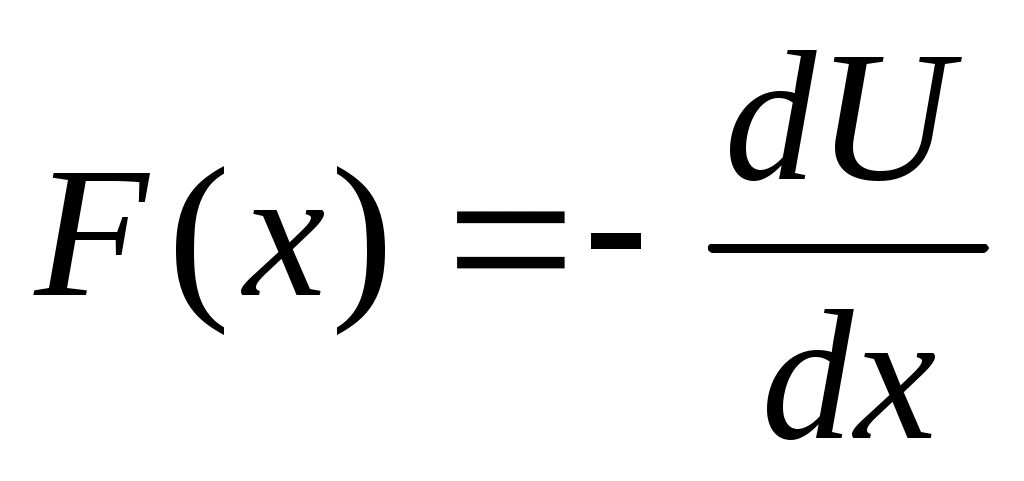 Интегрируем и вводим новую ф-ю. Интегрируем и вводим новую ф-ю. 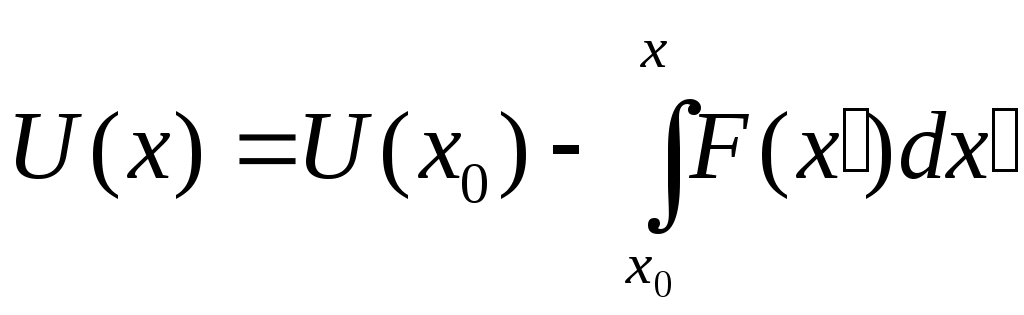 Эта ф-я наз-ся потенц. энергией. Эта ф-я наз-ся потенц. энергией. 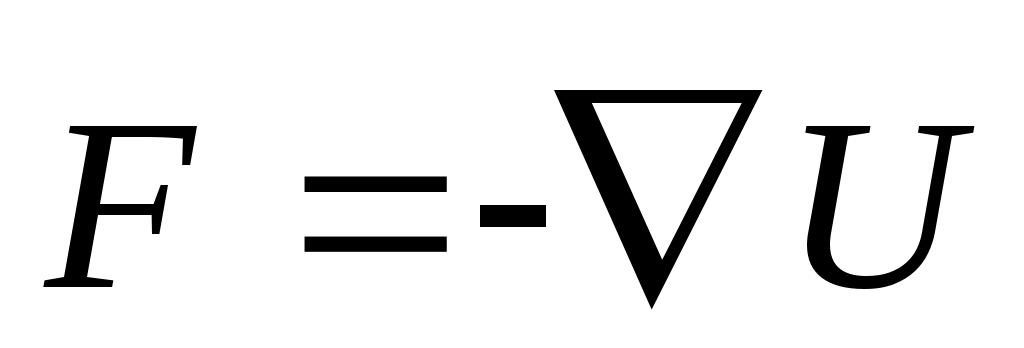 Другой вид при проектировании на Ох: Другой вид при проектировании на Ох: 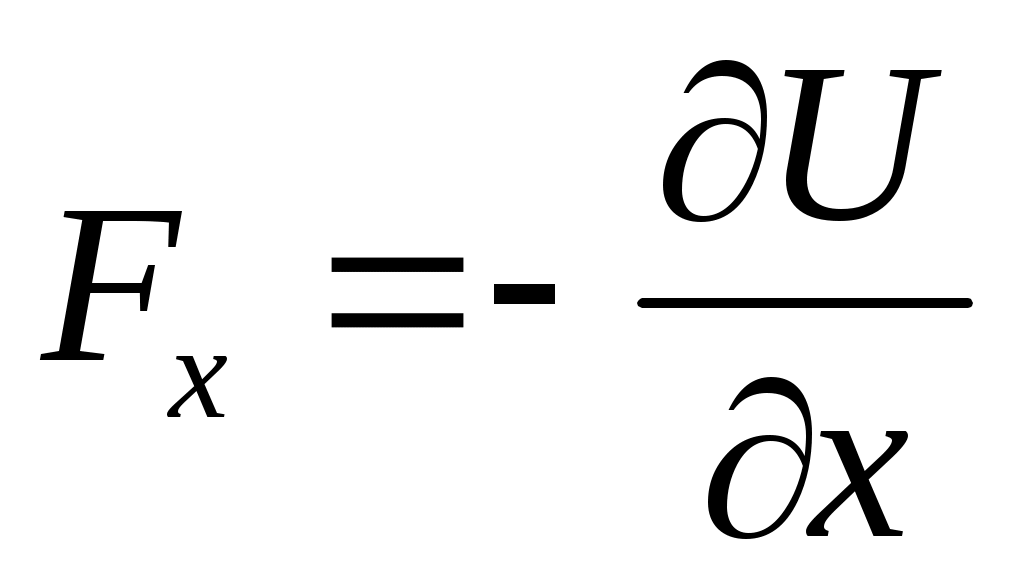 . Сила, которая может быть представлена в виде градиента потенц. энергии наз-ся потенц. энергией. В многомерном случае не всякая сила м.б. представлена в таком виде. Чтобы узнать явл-ся ли сила потенциальной, надо вычислить ротор. Если он во всех точках = 0, то сила является потенциальной. Но в одномерном случае любая интегрируемая сила зависящая от координаты является потенциальной. Наличие пот. силы означает, что имеет место закон сохранения энергии. . Сила, которая может быть представлена в виде градиента потенц. энергии наз-ся потенц. энергией. В многомерном случае не всякая сила м.б. представлена в таком виде. Чтобы узнать явл-ся ли сила потенциальной, надо вычислить ротор. Если он во всех точках = 0, то сила является потенциальной. Но в одномерном случае любая интегрируемая сила зависящая от координаты является потенциальной. Наличие пот. силы означает, что имеет место закон сохранения энергии. 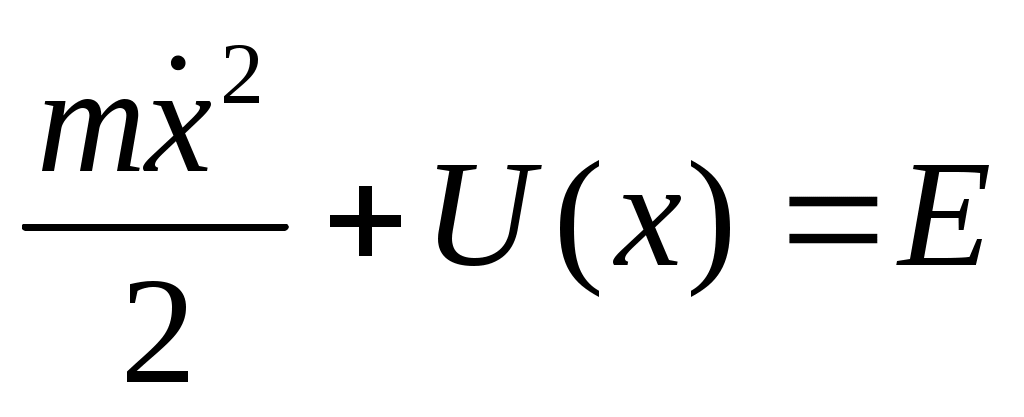 Он получается т.о.: берется ур-е Ньютона в таком виде: Он получается т.о.: берется ур-е Ньютона в таком виде: 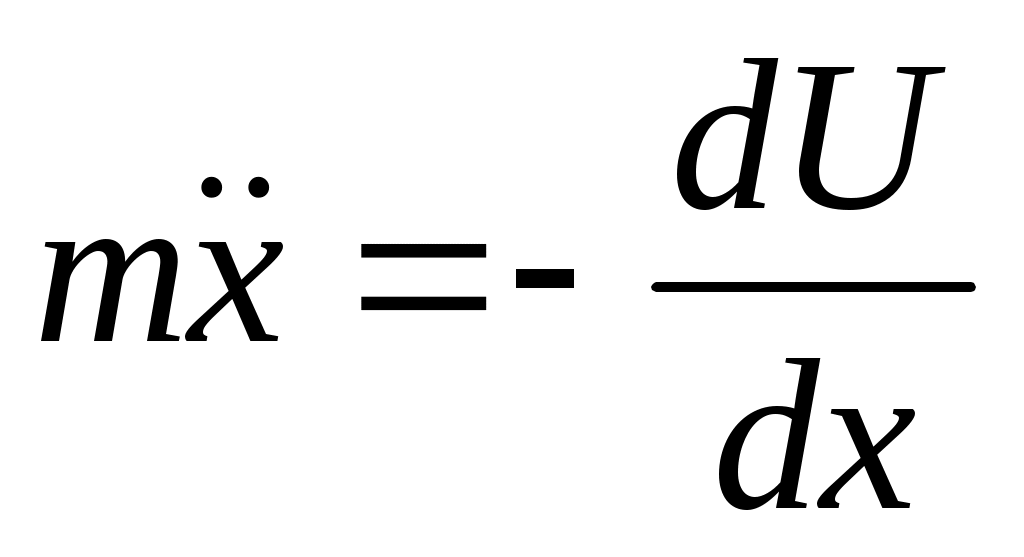 , умножая на dx: , умножая на dx: 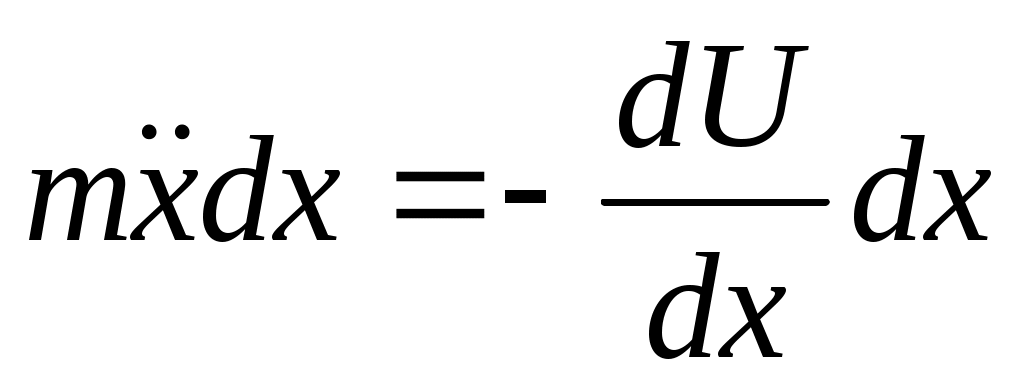 . Лев. часть переписывается в виде: . Лев. часть переписывается в виде: 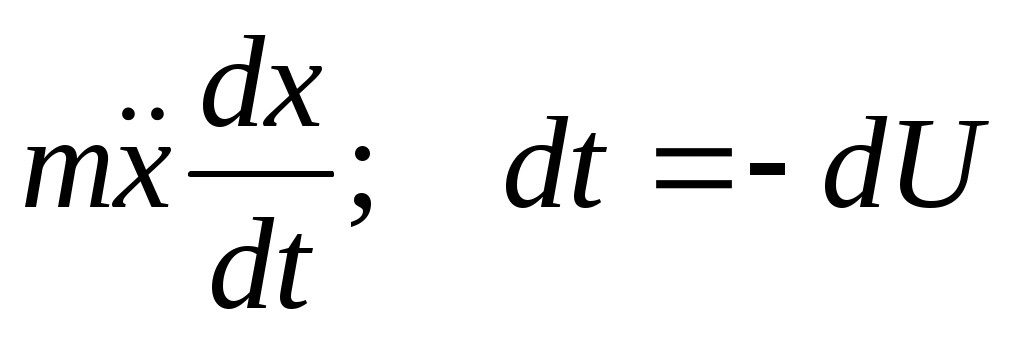 ; ;
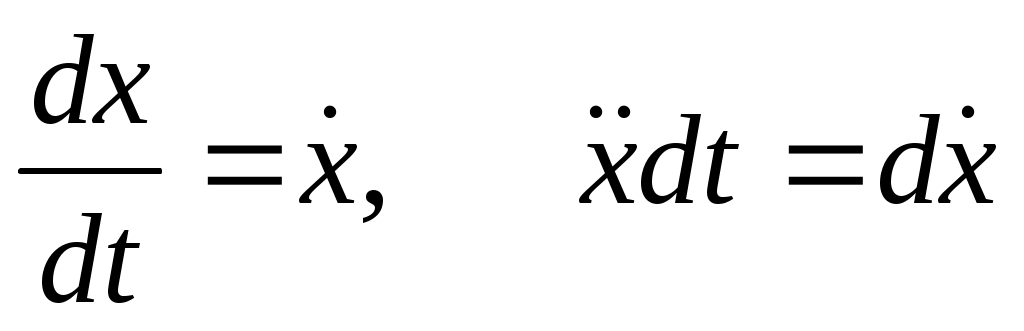 В итоге получается: В итоге получается: 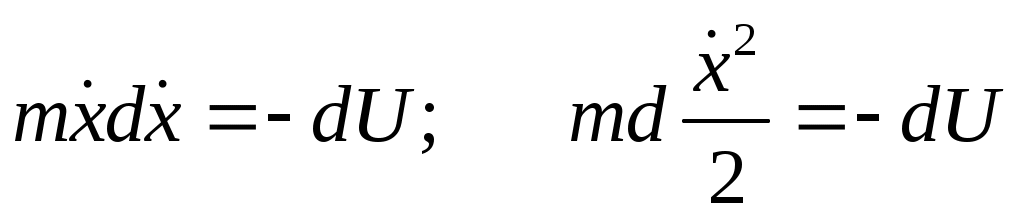 И общий диф-ал: И общий диф-ал: 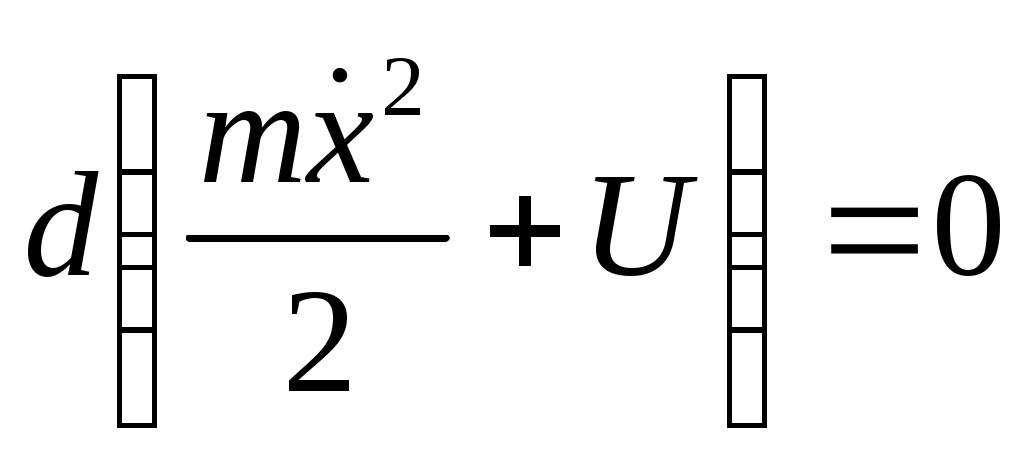 ф-я постоянна, т.к. диф-ал = 0. ф-я постоянна, т.к. диф-ал = 0. 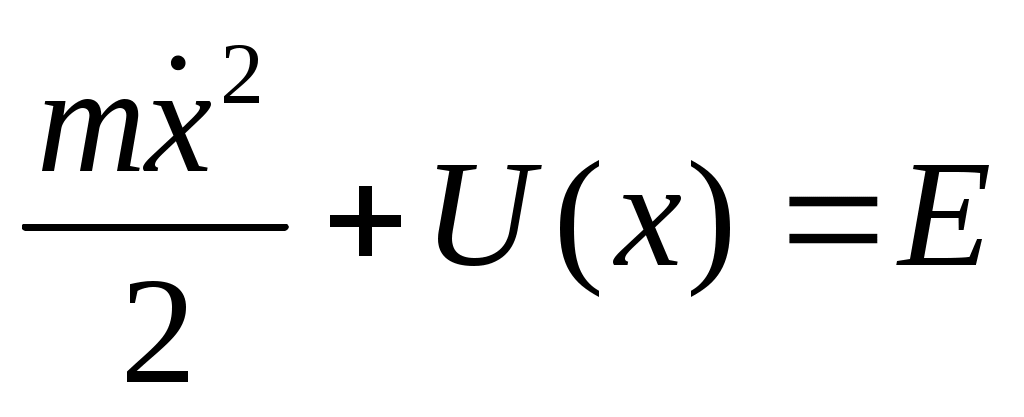 полная энергия. Закон сохранения энергии нужен для решения ур-я: полная энергия. Закон сохранения энергии нужен для решения ур-я: 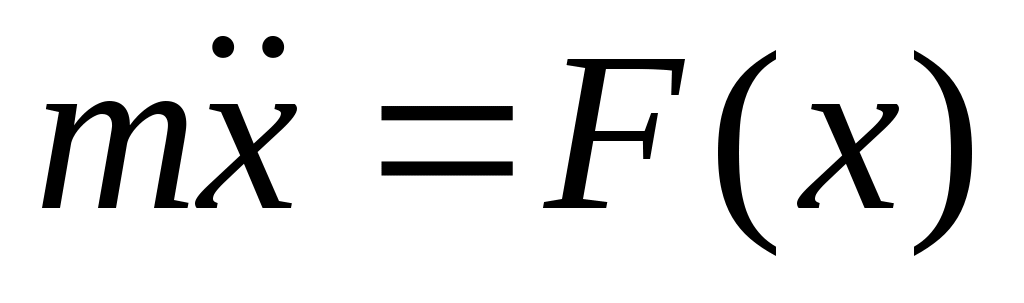 Здесь старшая производная 1-го порядка, то можно разделить переменные Здесь старшая производная 1-го порядка, то можно разделить переменные 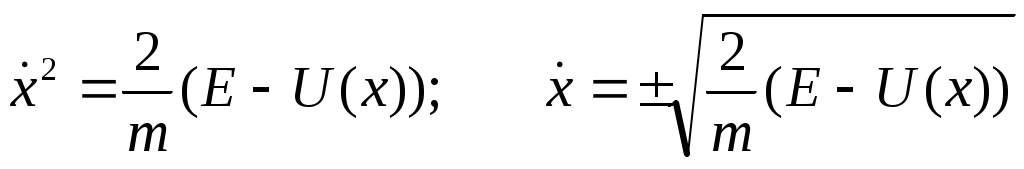 ; ;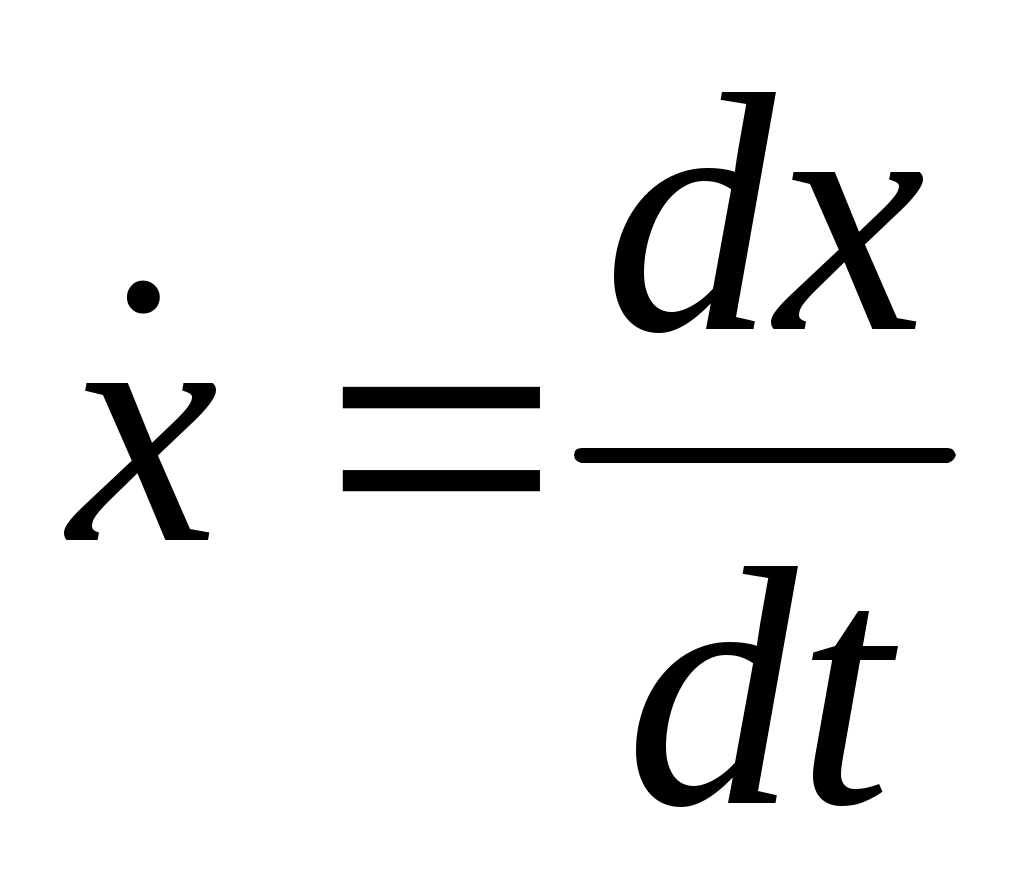
dt переносим направо: 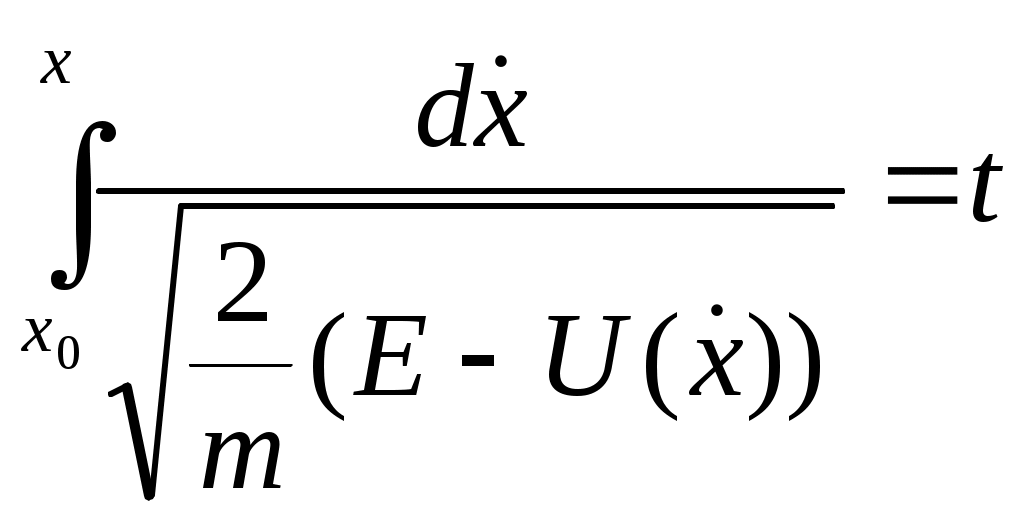 . Получили зависимость t от x. Найдем обратную ф-ю x = f-1(t)— это и есть решение задачи. Отметим св-ва корня. Е-U: кинет. энергия mv2/2. Массу сократили, осталось v2 извлекли корень, получили v. По определению скорости dx=vdt. Корень — абс. величина ск-ти, заданная как ф-я координаты. Знак + или – определяет направление движения. . Получили зависимость t от x. Найдем обратную ф-ю x = f-1(t)— это и есть решение задачи. Отметим св-ва корня. Е-U: кинет. энергия mv2/2. Массу сократили, осталось v2 извлекли корень, получили v. По определению скорости dx=vdt. Корень — абс. величина ск-ти, заданная как ф-я координаты. Знак + или – определяет направление движения.
1.5. Классификация одномерных движений.
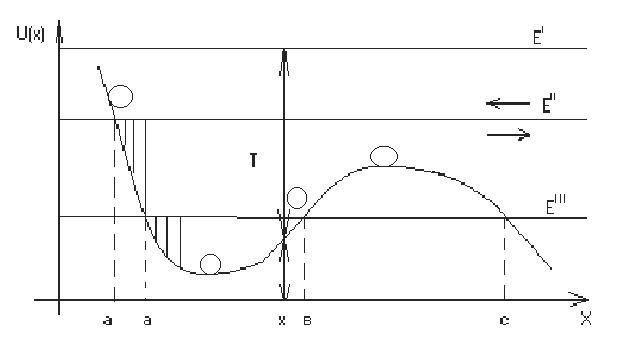
Положения равновесия: устойчивое, неустойчивое.
Кинетич. энергия: 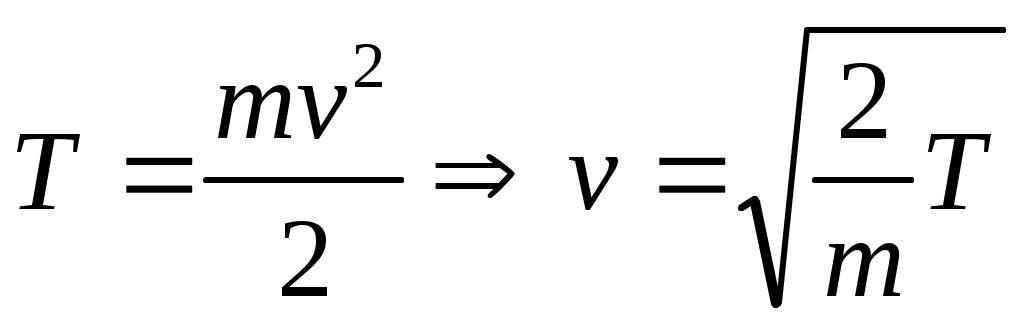 . Потенц. энергия как ф-я координат. сила каждой точки . Потенц. энергия как ф-я координат. сила каждой точки 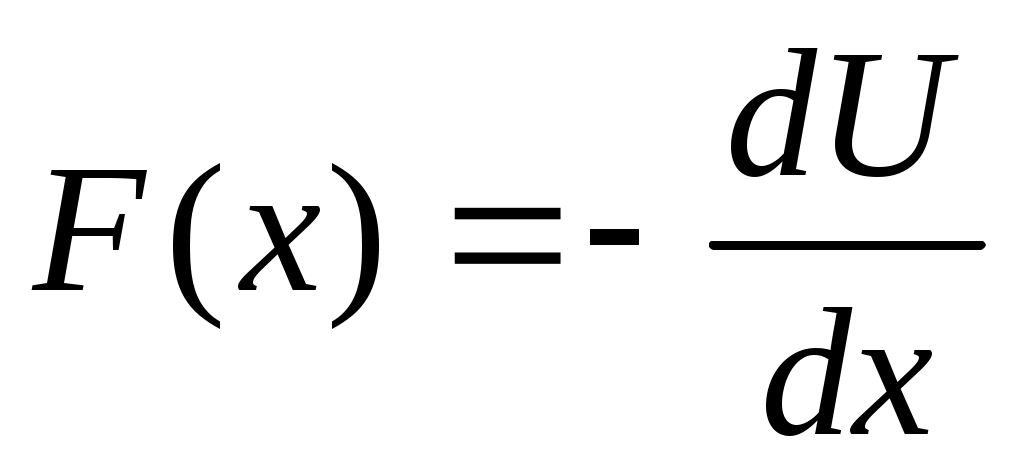 . Инфинитное движение — уходит и приходит из бесконечности. Точки a, в, с удовлетворяют ур-ю: U(a)=E, U(в)=E, U(с)=E. . Инфинитное движение — уходит и приходит из бесконечности. Точки a, в, с удовлетворяют ур-ю: U(a)=E, U(в)=E, U(с)=E.
Отрезок [а,в] — потенциальная яма. Движение финитное.
Отрезок [в,с]: разность м\д полной энергией и потенц. — отрицательна. Эта область не имеет физич. смысла. Это потенц. барьер. Частица не может его пройти. Имея дело с малыми частицами, там возникают специфические свойства: потенц. барьер становится полупрозрачным — туннелирование. В случае финитного движения в потенц. яме движение периодическое. Скорость в точке х: 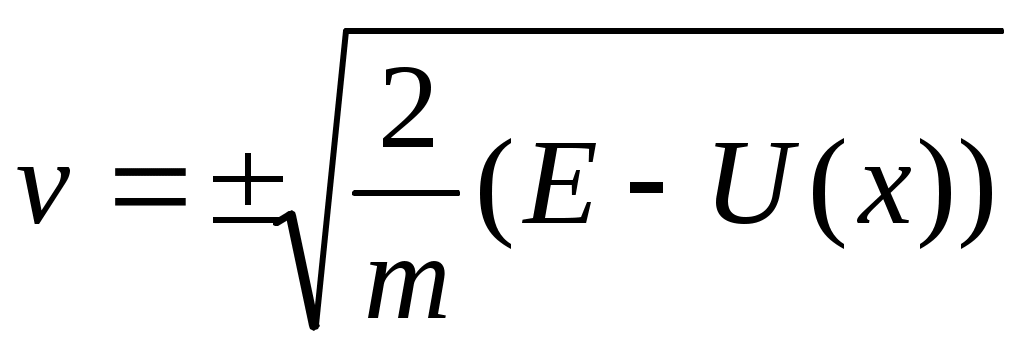 (*) если она фиксирована, то скорость изменяется только по знаку. (*) если она фиксирована, то скорость изменяется только по знаку. 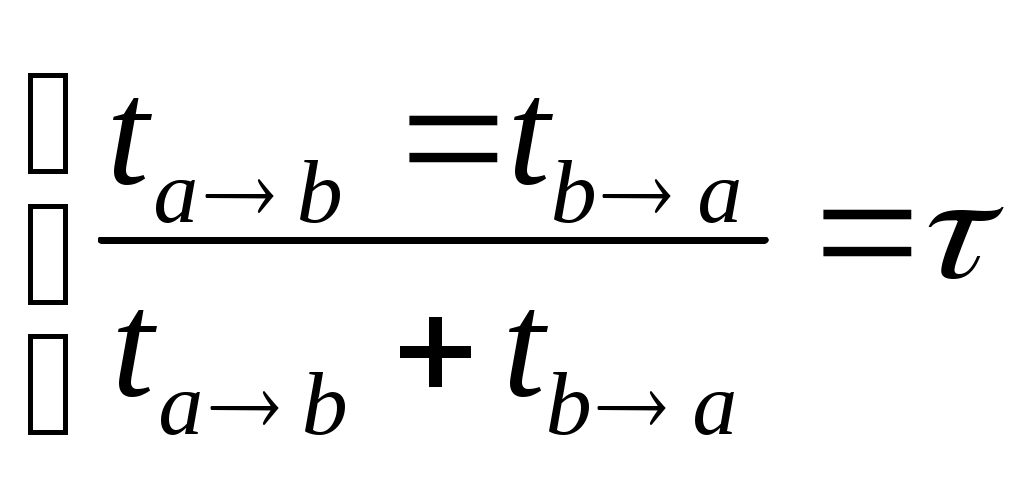 период — время м\д уходом и возвращением в точку а. период — время м\д уходом и возвращением в точку а. 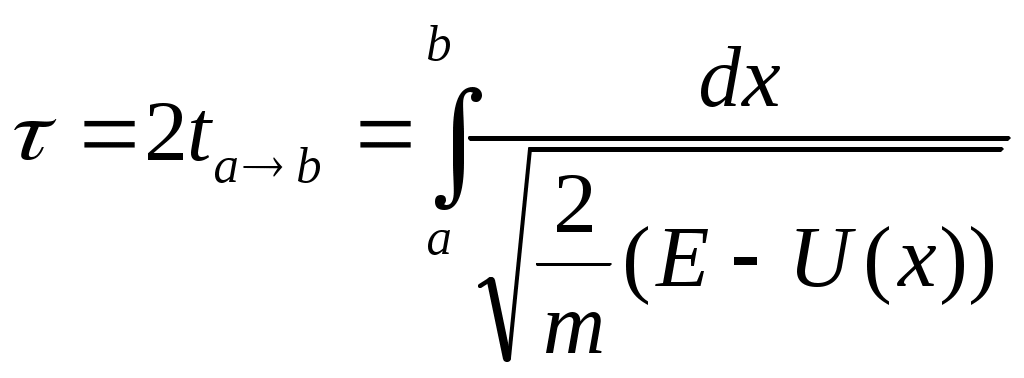 Из (*) найдем dt. Из (*) найдем dt.
7.1. Понятие связи.
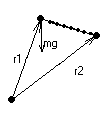 1 k k — пружина. Пусть 1 k k — пружина. Пусть  и в и в
2 пределе она превращается в
жесткий стержень длиной ℓ.
Чтобы задать положение такой
системы: 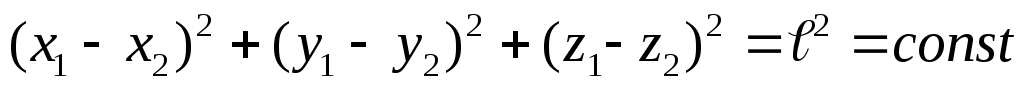 если стержень не сжимают. если стержень не сжимают.
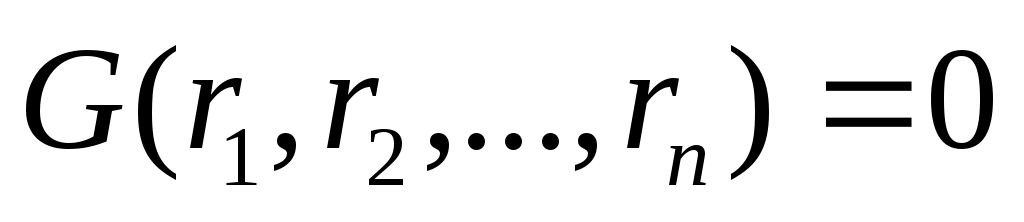 — голономная связь. — голономная связь.
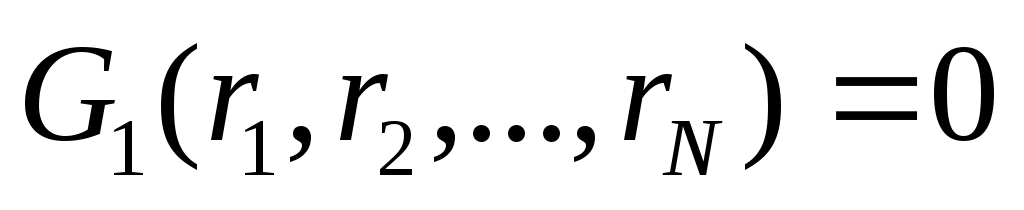 S-уравнений, S-уравнений,
… S голономных связей
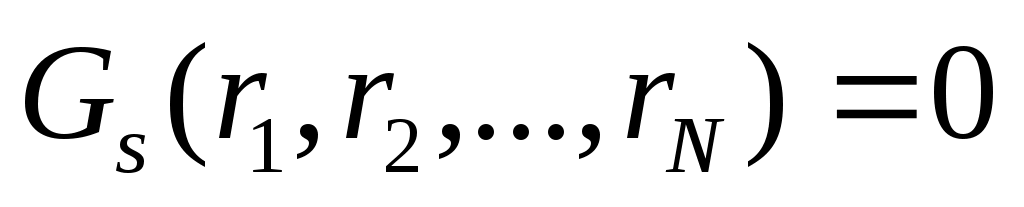
7.2. Принцип Даламбера.
Пусть есть N частиц. 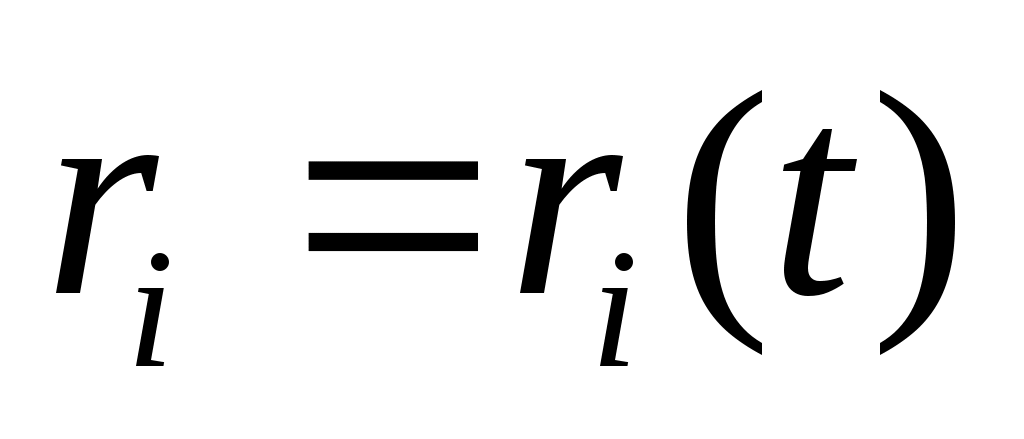 меняется. Его изменение за dt: меняется. Его изменение за dt: 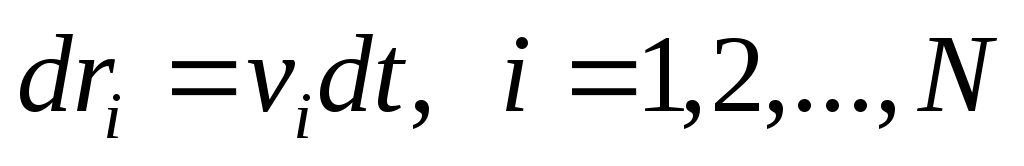 . .
1. Координата и ее перемещение зависит от начальных условий.
2. Реальное перемещение частиц удовлетворяет уравнениям движения.
3. Эти приращения должны быть совместимы со связями.
Введем новый термин «виртуальные перемещения» «ВП» 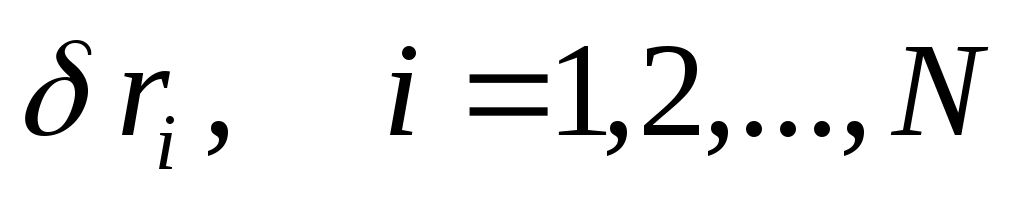 . .
1. Не зависят от начальных условий. 2. Не удовлетворяют уравнениям перемещения. 3. Рассматриваются как мгновенные перемещения. 4. Должны быть совместимы со связями.
Рассмотрим самый пред. случай, когда связь G(x1,x2)=0. Дадим системе ВП так, что 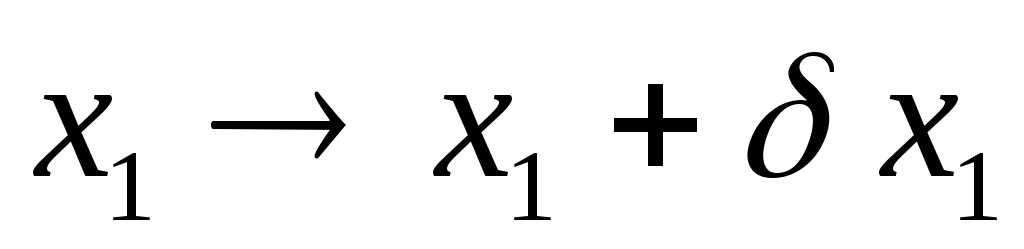 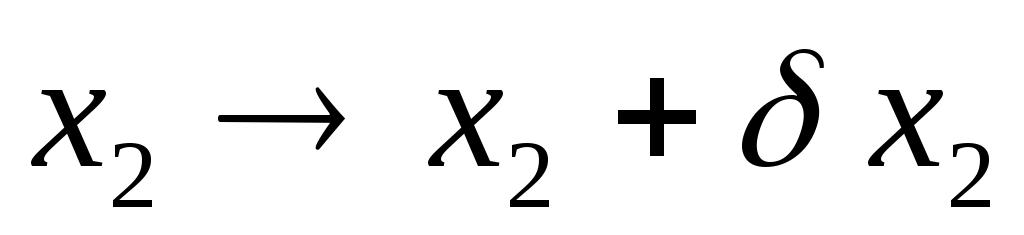 . Эти ВП должны быть совместимы со связями G(x1,x2); . Эти ВП должны быть совместимы со связями G(x1,x2); 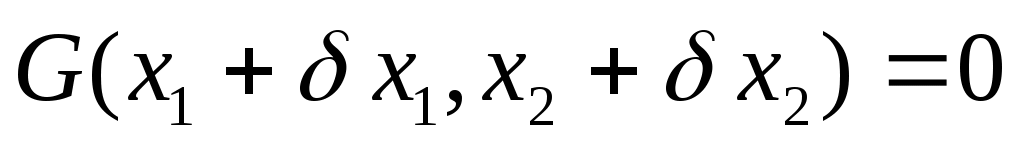 . Разложим левую часть в ряд: . Разложим левую часть в ряд: 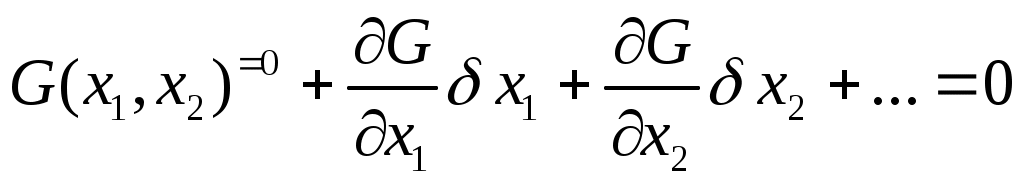 Осталась сумма: Осталась сумма: 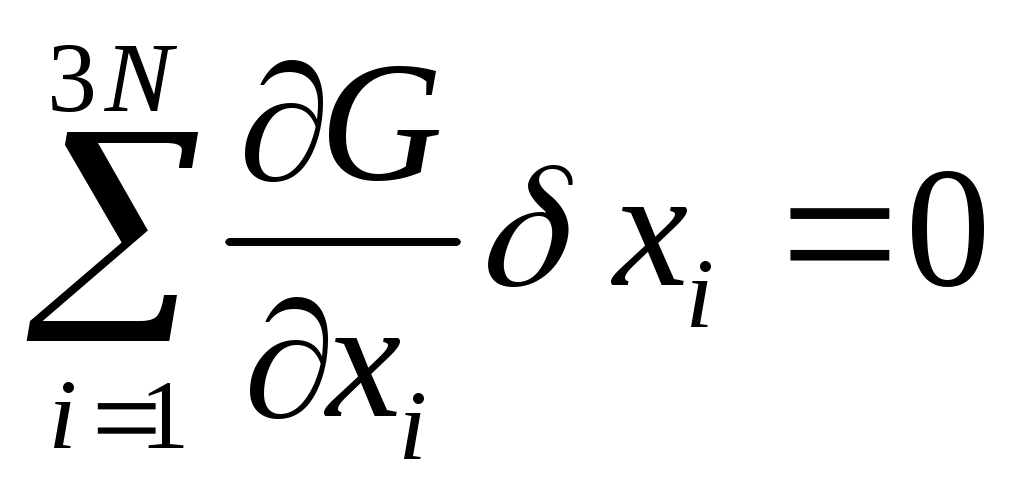 . Пусть k=1,2,…,S. Каждой связи соответствует своя функция Gk. Для каждой функции свое уравнение. Введем обозначение: . Пусть k=1,2,…,S. Каждой связи соответствует своя функция Gk. Для каждой функции свое уравнение. Введем обозначение: 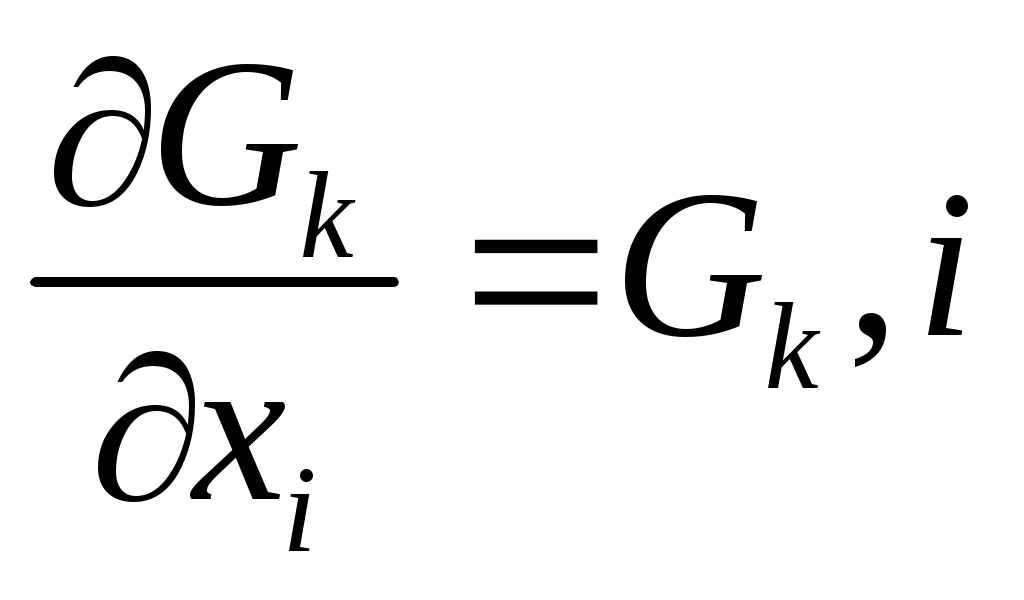 (i — по какой координате частная производная). (i — по какой координате частная производная). 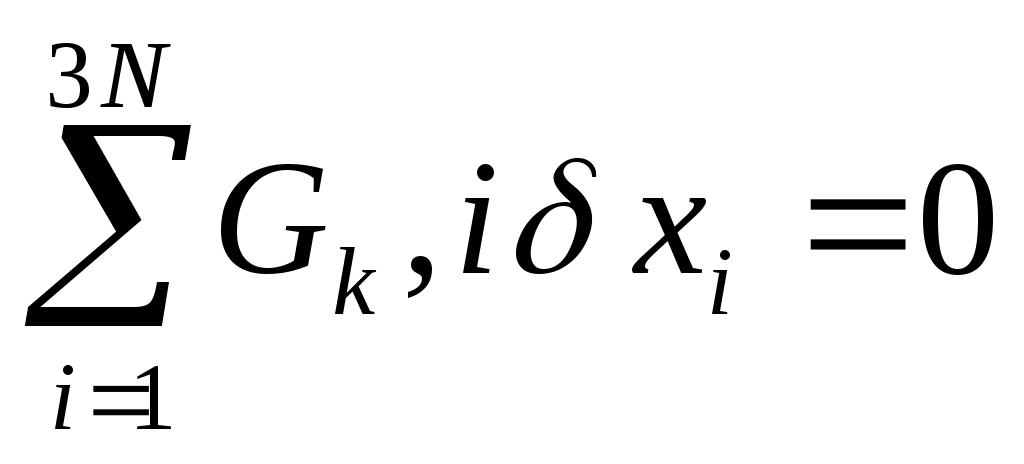 . Рассмотрим простейший случай связи: . Рассмотрим простейший случай связи:
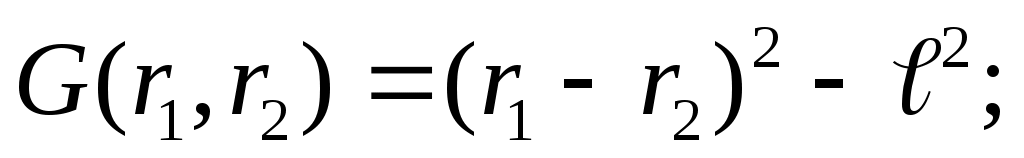 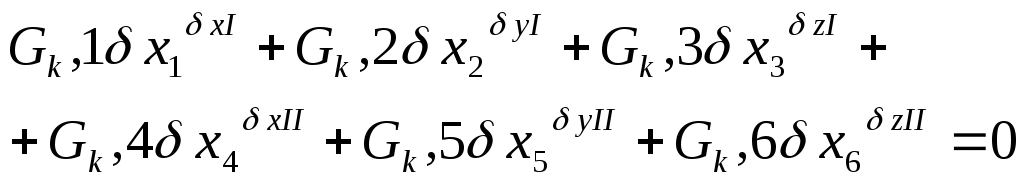 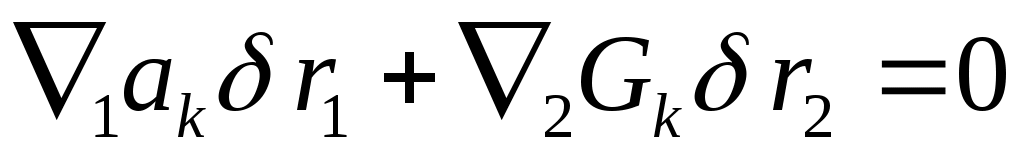 Вычислим град. от G. Вычислим град. от G. 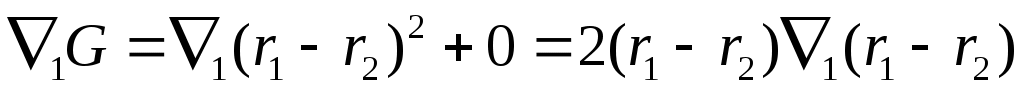 ; ;
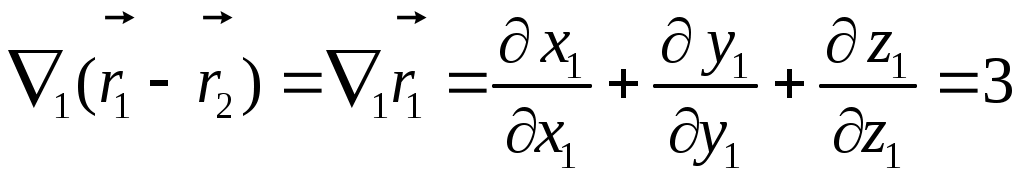
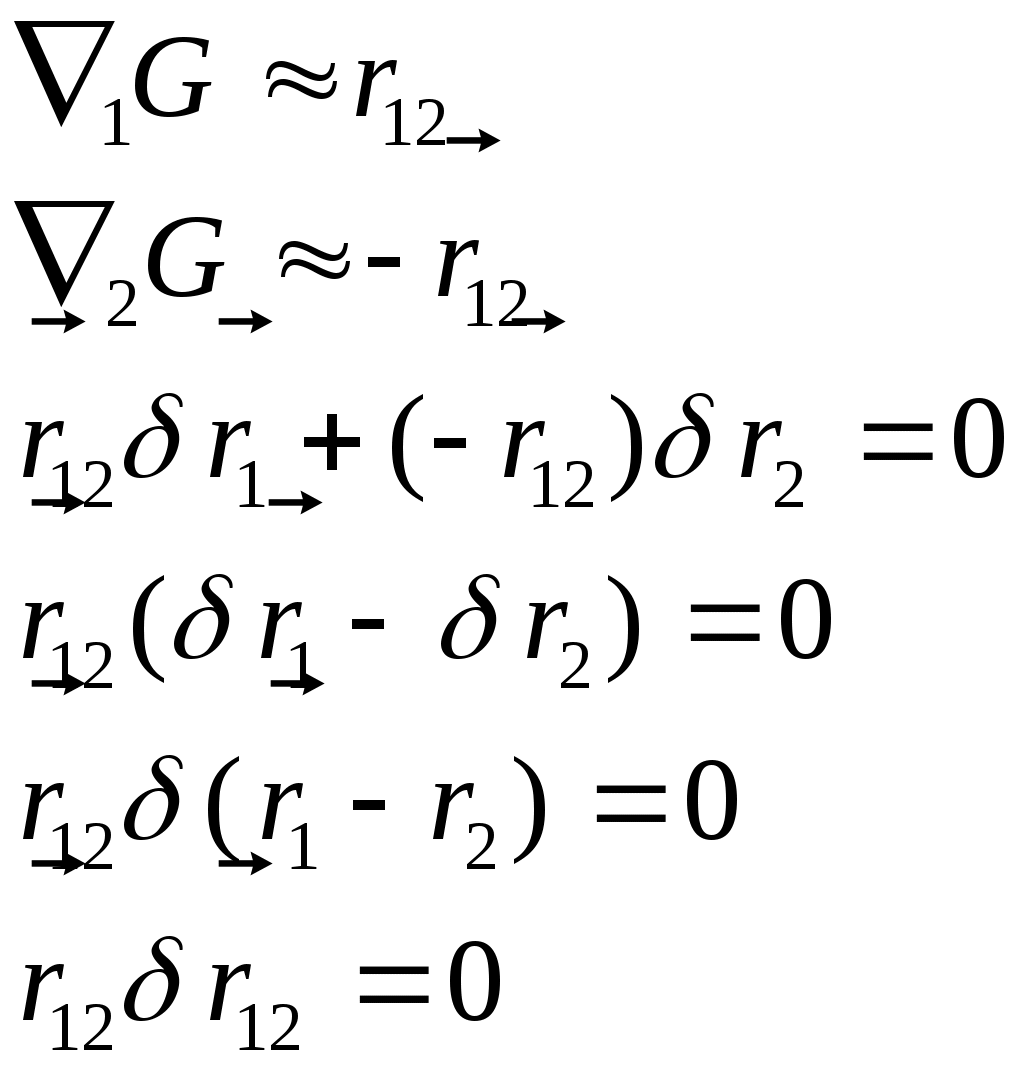 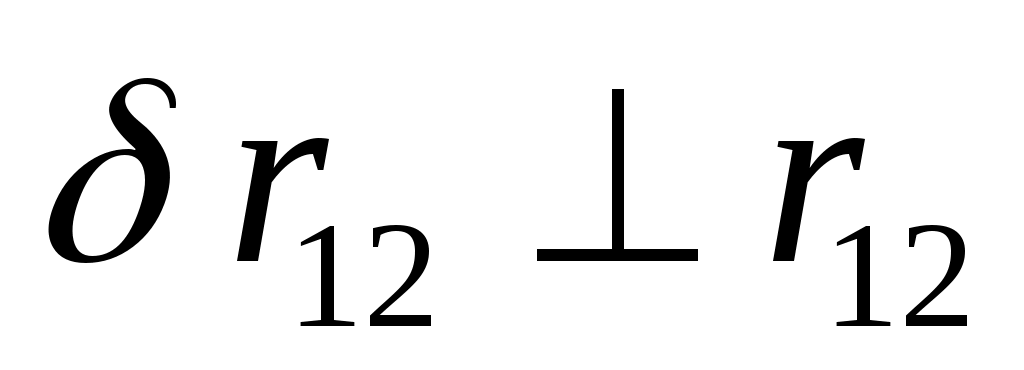 Пусть между двумя точками д-ет центр. сила, кот.направлена вдоль 12. Вирт. раб., совершаемая реакциями связи = 0. Это положение, распространяемое на все механич. системы, называется принципом Даламбера. Пусть между двумя точками д-ет центр. сила, кот.направлена вдоль 12. Вирт. раб., совершаемая реакциями связи = 0. Это положение, распространяемое на все механич. системы, называется принципом Даламбера.
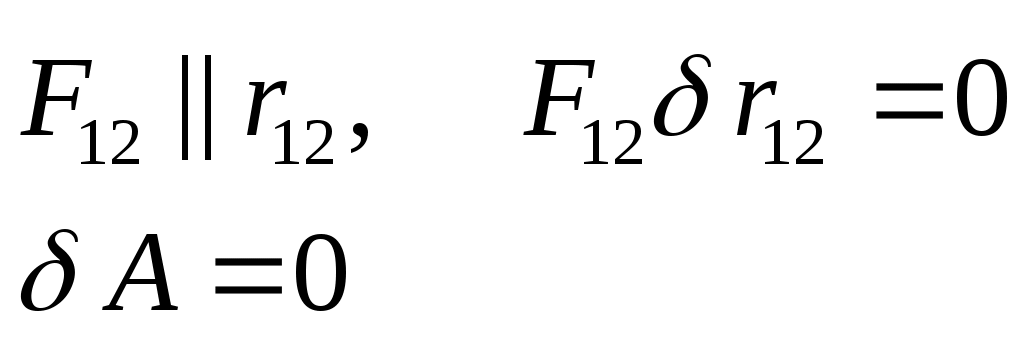 F12 — реакция связи со стороны стержня на м.т. F12 — реакция связи со стороны стержня на м.т.
7.3.Уравнение Лагранжа I рода.
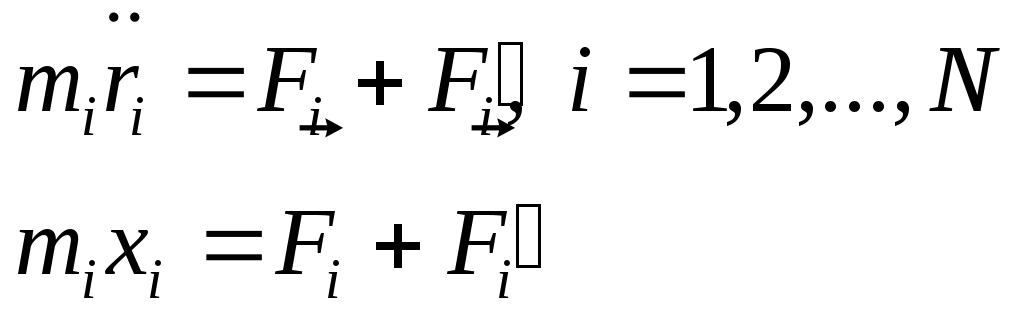 Чтобы уменьшить число неизвестных используем ур-е связи: Чтобы уменьшить число неизвестных используем ур-е связи: 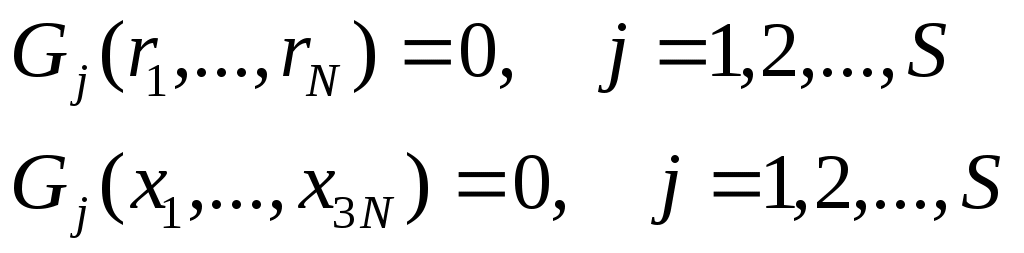 Выражение для ВП: Выражение для ВП: 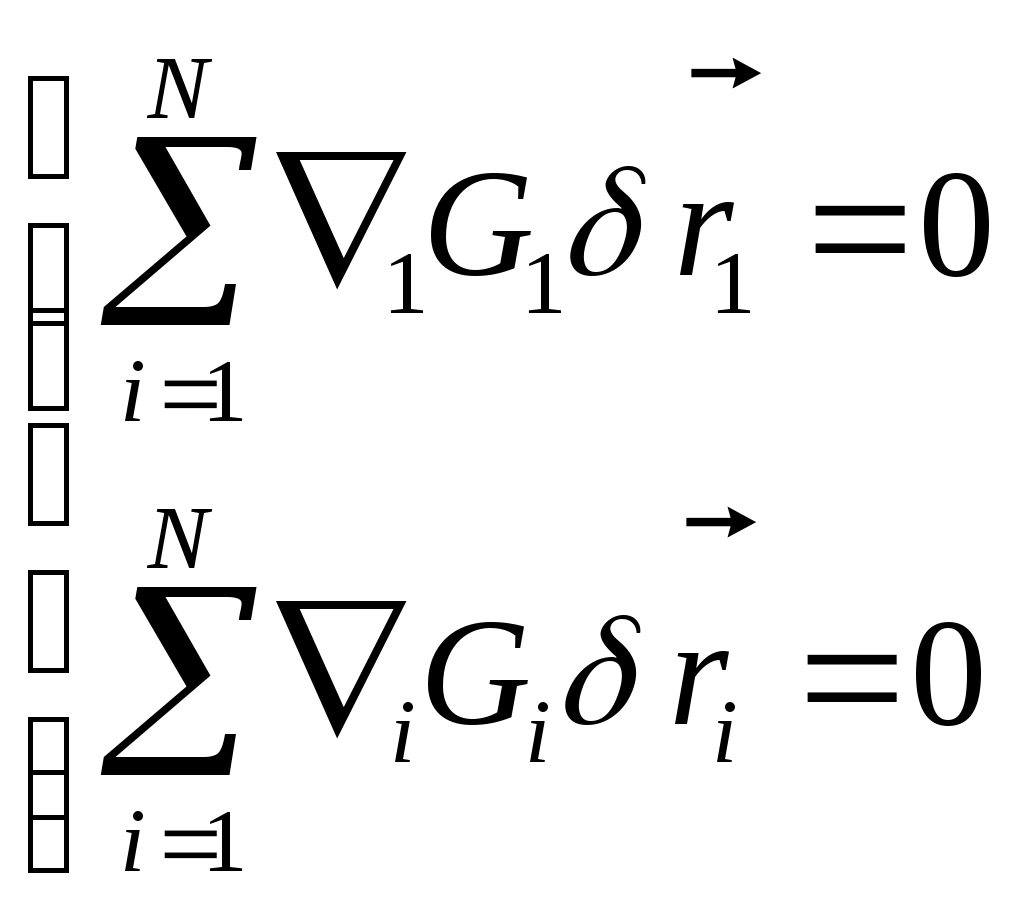 Показ. связь м\д ВП. Перепишем их в скалярной форме. Показ. связь м\д ВП. Перепишем их в скалярной форме. 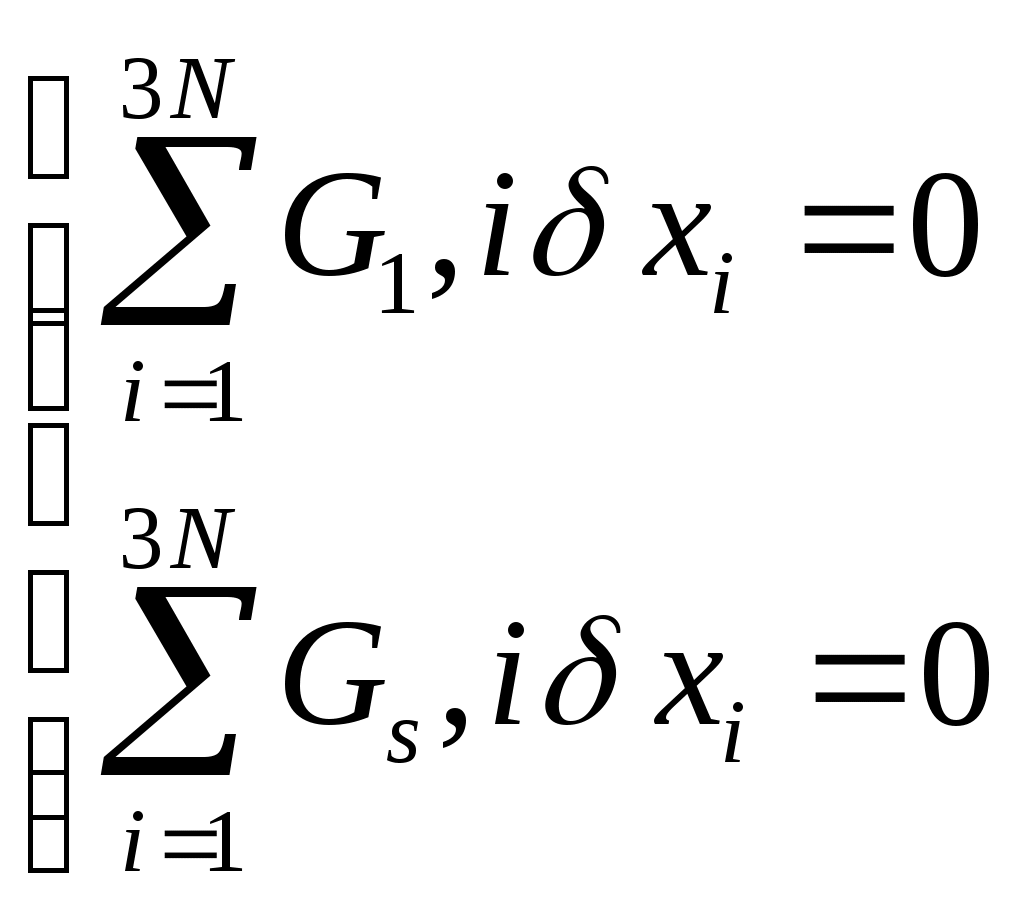 Добавилось еще S ур-ий. Всего 6N неизвестных, 3N+S ур-ий. Чтобы число уравнений совпало с числом неизвестных исп-ем пр-п Даламбера. Вирт. раб. сил реакций: Добавилось еще S ур-ий. Всего 6N неизвестных, 3N+S ур-ий. Чтобы число уравнений совпало с числом неизвестных исп-ем пр-п Даламбера. Вирт. раб. сил реакций: 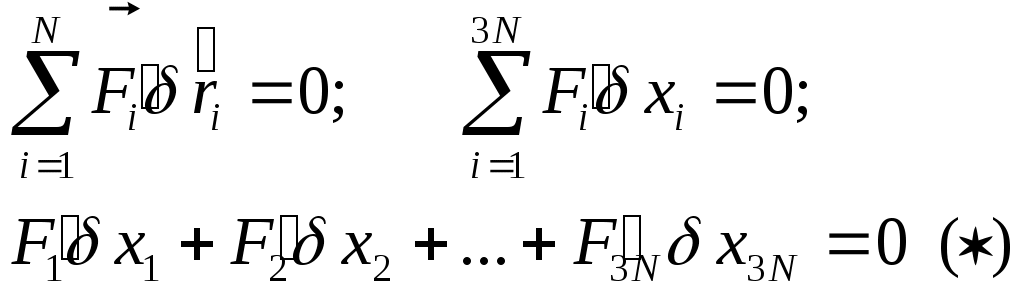 Если бы δxi , были независимы, то (*) было бы 3N ур-ий, но они не все независимы. Из 3N вариаций δxi независимых только 3N-S. 3N+S+3N-S=6N независимых переменных. Т.о. можно решить сист. ур-ий. x1,…,x3N переменных, F’1,…,F3N. Пр-п Даламбера: Если бы δxi , были независимы, то (*) было бы 3N ур-ий, но они не все независимы. Из 3N вариаций δxi независимых только 3N-S. 3N+S+3N-S=6N независимых переменных. Т.о. можно решить сист. ур-ий. x1,…,x3N переменных, F’1,…,F3N. Пр-п Даламбера: 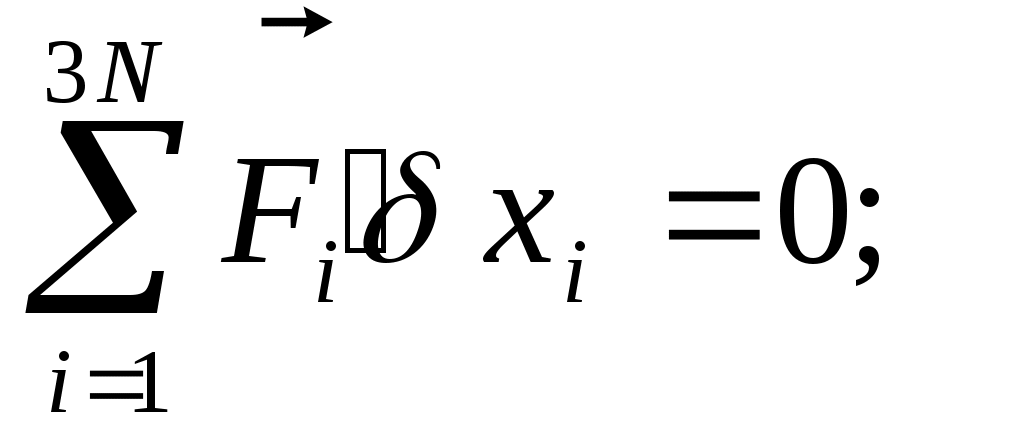 . . 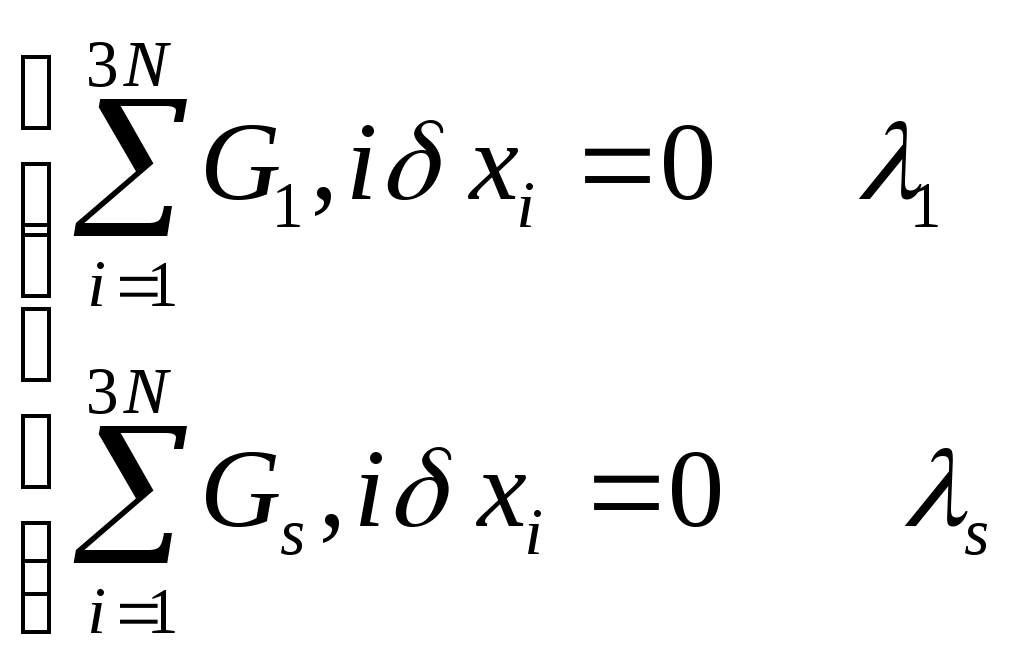
Берем любое λ для получения симметричной формы ур-я (чтобы выделить зависимые и независимые переменные). Получим: 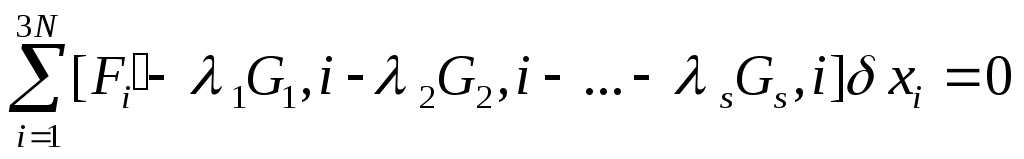 Разделим сумму на 2 части: Разделим сумму на 2 части:
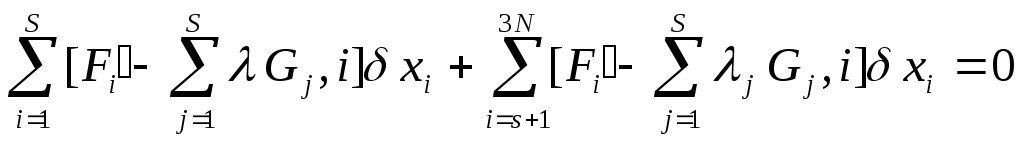 Ввели неопределенный множитель λj = количеству связей — неопределенные множители Лагранжа. запишем ур-я дв-я со связями в сим. виде. Из δxi (i=1,…,3N) независимыми является 3N-S переменных, а S зависимы от других. Выберем λ таким, чтобы все квадратные скобки I части суммы обратились в 0, при i=1,…, S. Ввели неопределенный множитель λj = количеству связей — неопределенные множители Лагранжа. запишем ур-я дв-я со связями в сим. виде. Из δxi (i=1,…,3N) независимыми является 3N-S переменных, а S зависимы от других. Выберем λ таким, чтобы все квадратные скобки I части суммы обратились в 0, при i=1,…, S. 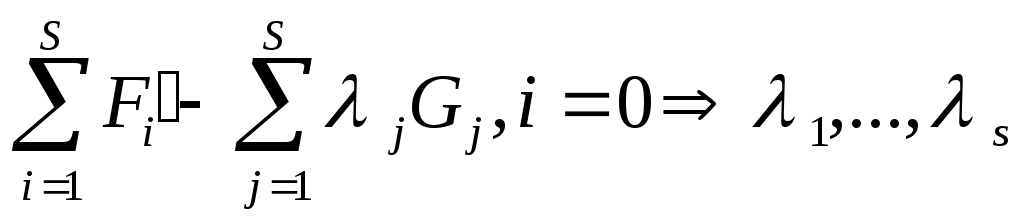 т.к. во II части суммы δxi независимы, то выберем δxS+1 не равным 0, а δx2…S =0, то т.к. во II части суммы δxi независимы, то выберем δxS+1 не равным 0, а δx2…S =0, то 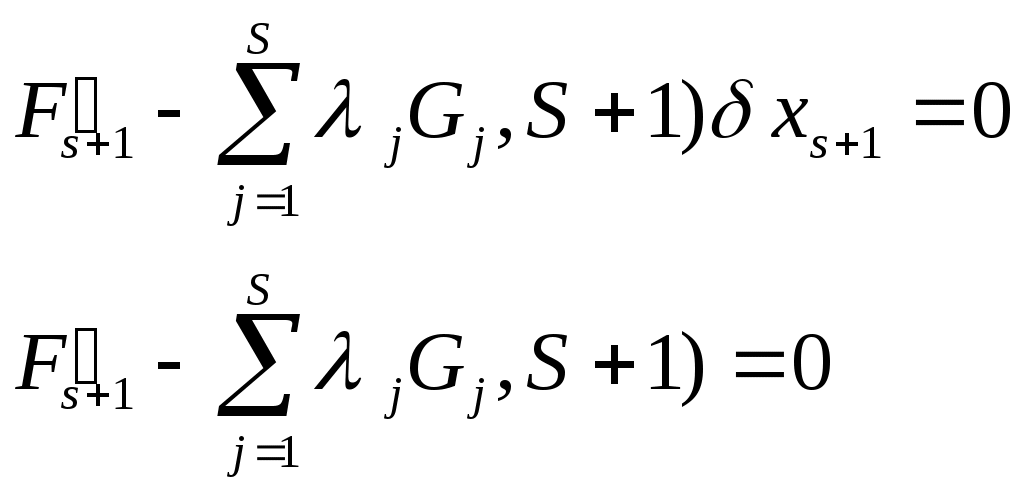 δxS+2 не равным 0 и т.д. Все эти компоненты удовлетворяют одному и тому же ур-ю. Запишем их в общем виде: δxS+2 не равным 0 и т.д. Все эти компоненты удовлетворяют одному и тому же ур-ю. Запишем их в общем виде: 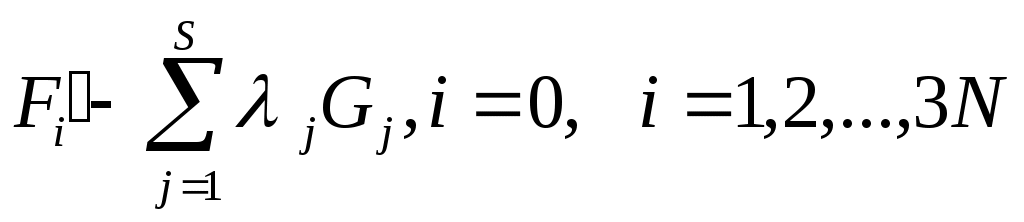 3N ур-ий. 3N+S неизвестных. Необходимо добавить еще S ур-ий для решения задачи. 3N ур-ий. 3N+S неизвестных. Необходимо добавить еще S ур-ий для решения задачи.
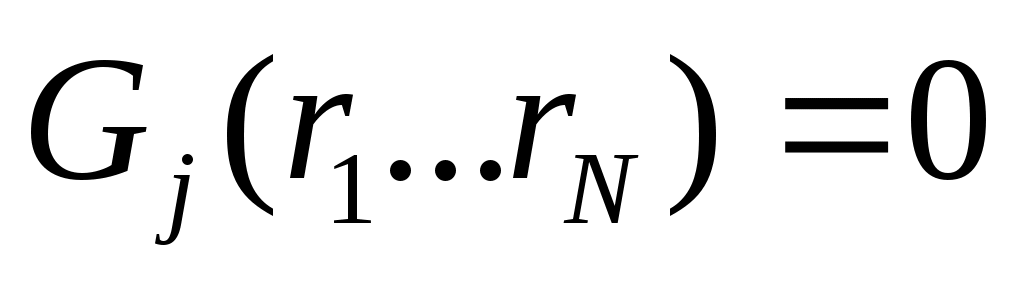 S ур-ий, т.е. S ур-ий связи. S ур-ий, т.е. S ур-ий связи.
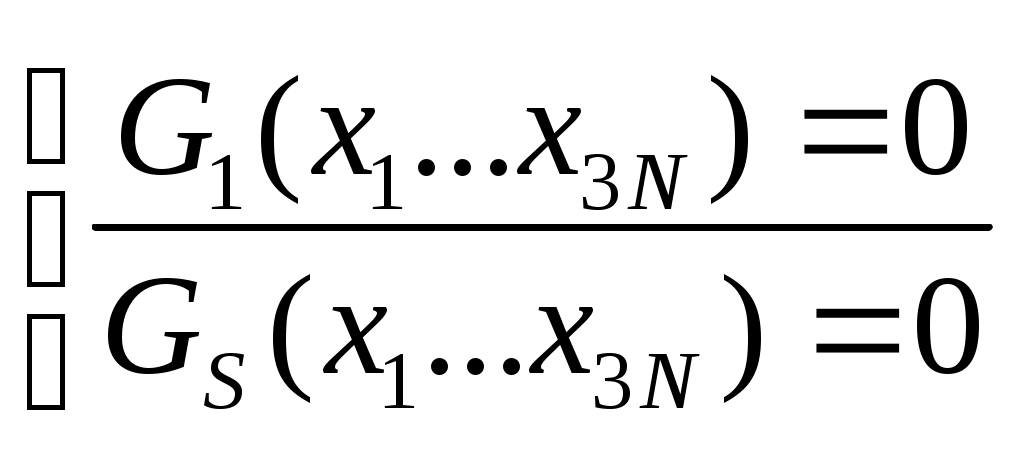 Перепишем. Перепишем.
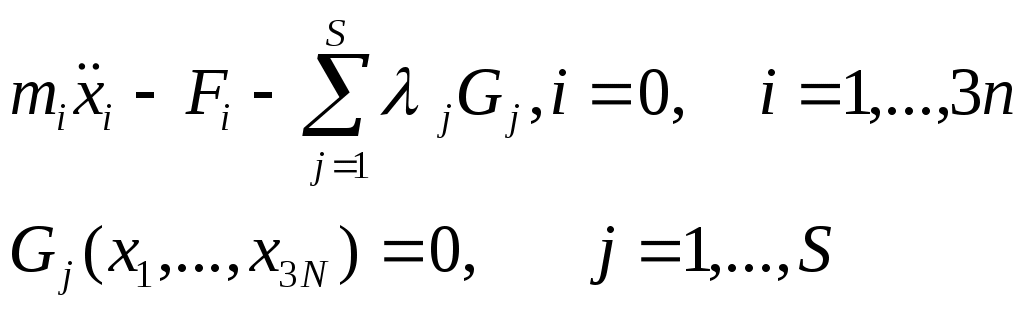 Ур-е Лагранжа I рода. Ур-е Лагранжа I рода.
8.1. Обобщенные координаты и скорость.
Существует мн-во координат. Найдем такое соотношение ур-я движения, для любой СК. Пусть 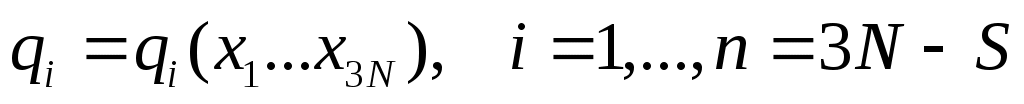 . 3N-S — число степеней свободы системы. qi — любая ЛНЗ пар-ры , через которые можно однозначно определить все координаты системы — обобщенные координаты. . 3N-S — число степеней свободы системы. qi — любая ЛНЗ пар-ры , через которые можно однозначно определить все координаты системы — обобщенные координаты.
Обобщ. корд-ты — любой набор 3N-S пар-ров, позволяющих однозначно определить положение системы в любой момент времени. 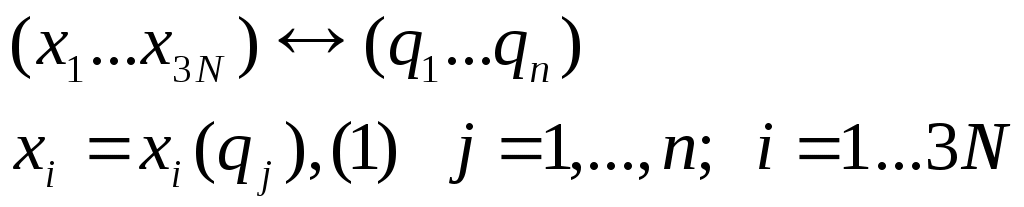 Леммы Леммы
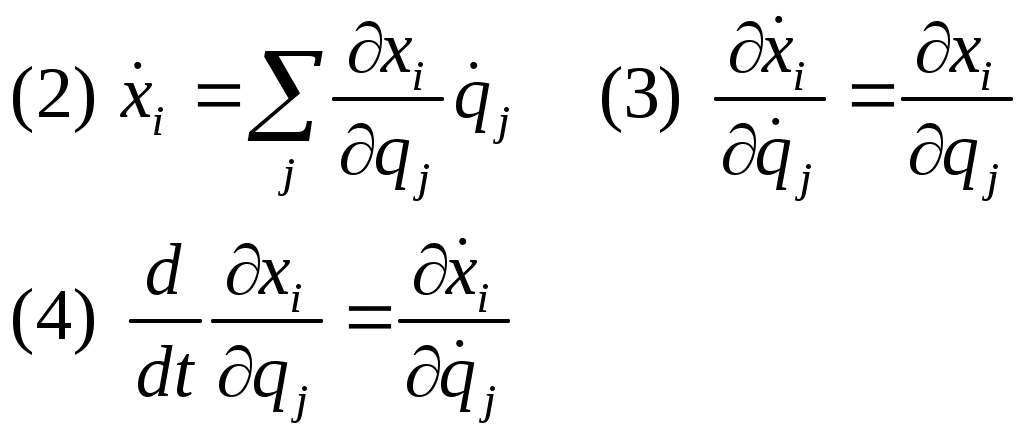 Если система движется, то все qj явл-ся функциями времени, тогда xi, зависящее от qj зависящих от t, то декартовы координаты тоже будут зависеть от t. Если система движется, то все qj явл-ся функциями времени, тогда xi, зависящее от qj зависящих от t, то декартовы координаты тоже будут зависеть от t. 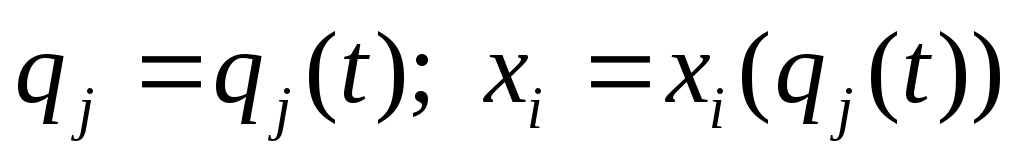
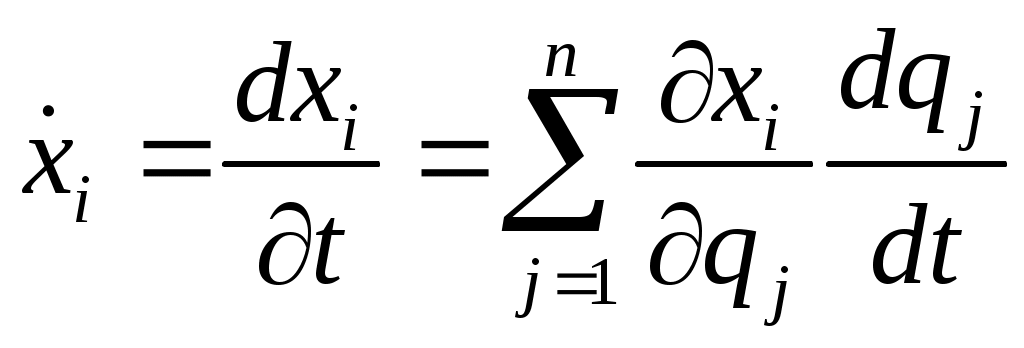 произв. сл. ф-ии. произв. сл. ф-ии.
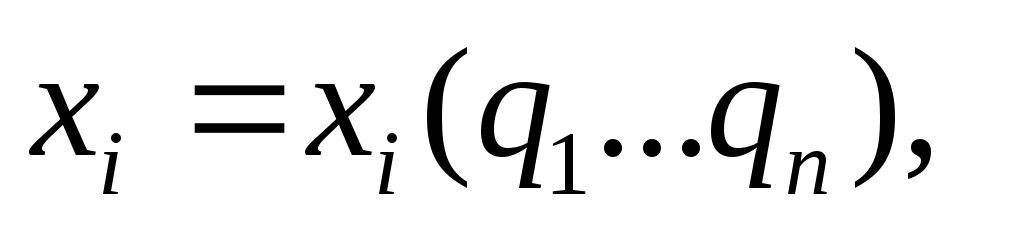 Когда будем брать приращение в процессе движения, то получим: Когда будем брать приращение в процессе движения, то получим:
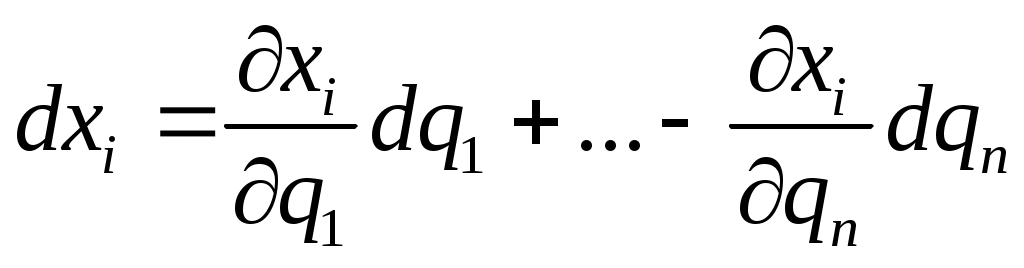 делим на dt: делим на dt:
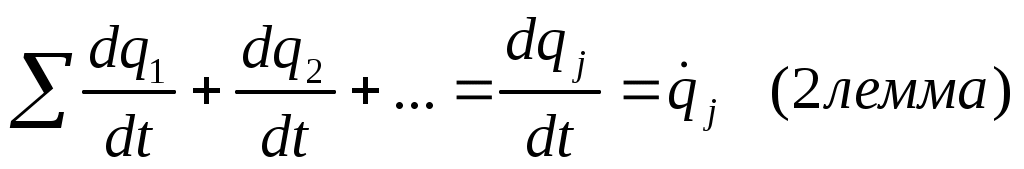 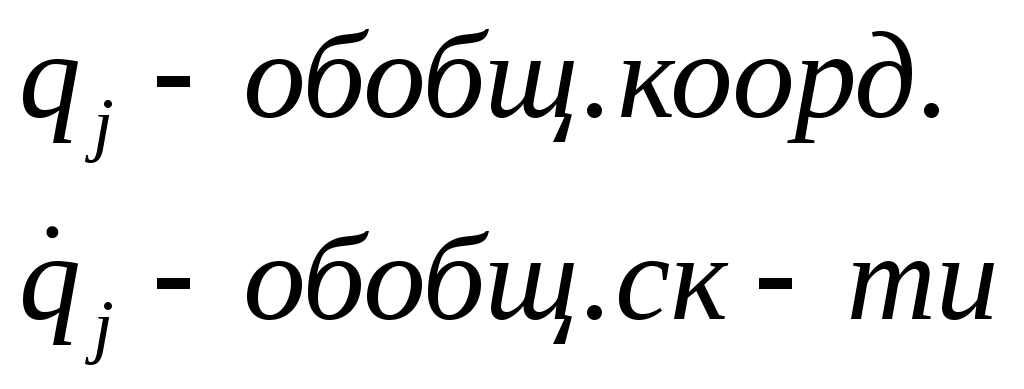
Возьмем (2 лемма) и диф-ем по dt и записываем:
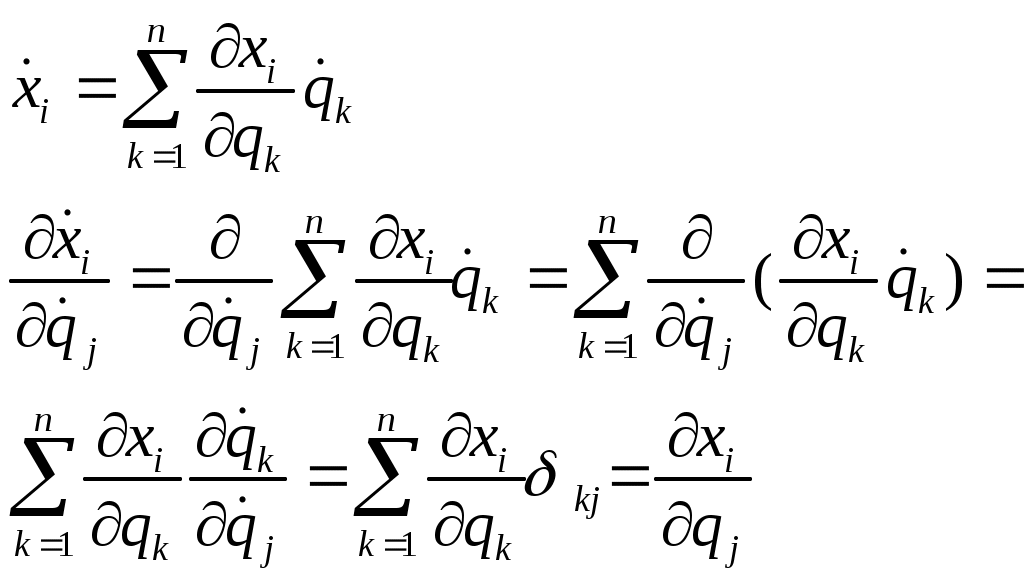 (3 лемма). (3 лемма).
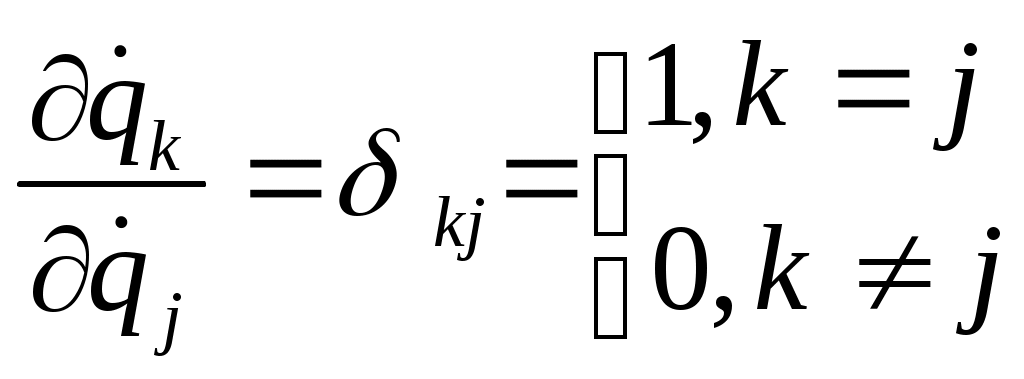 символ Кронекера. символ Кронекера.
8.2. Работа и энергия в обобщенных координатах.
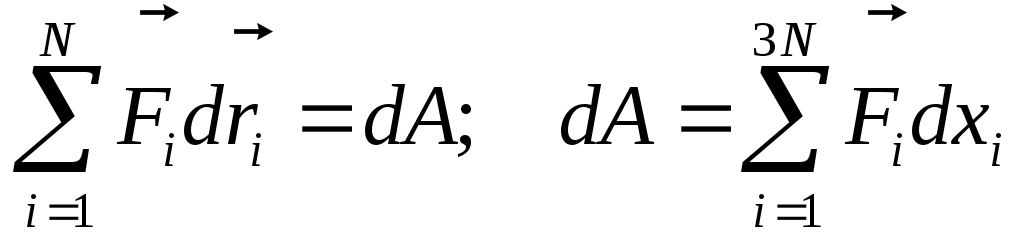 За dt координата изменится на dxi и взяв скал. произведение на силу, получим работу. За dt координата изменится на dxi и взяв скал. произведение на силу, получим работу.
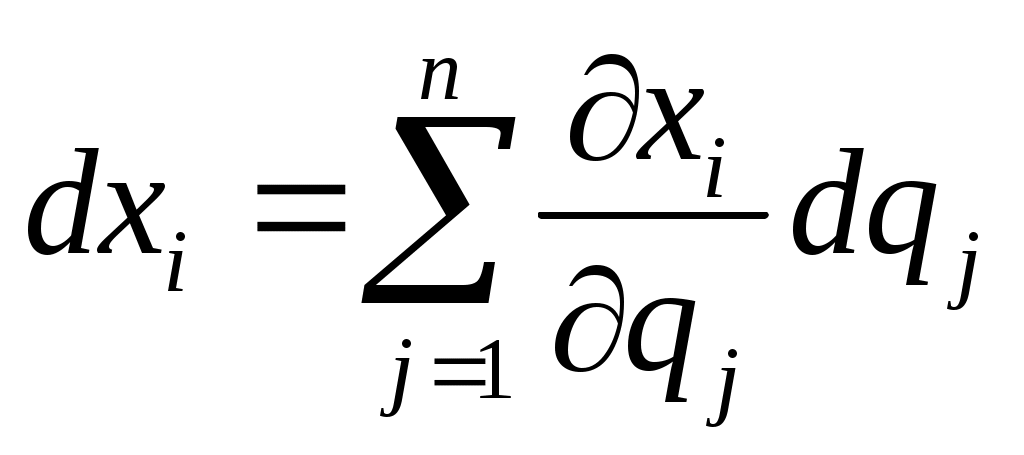 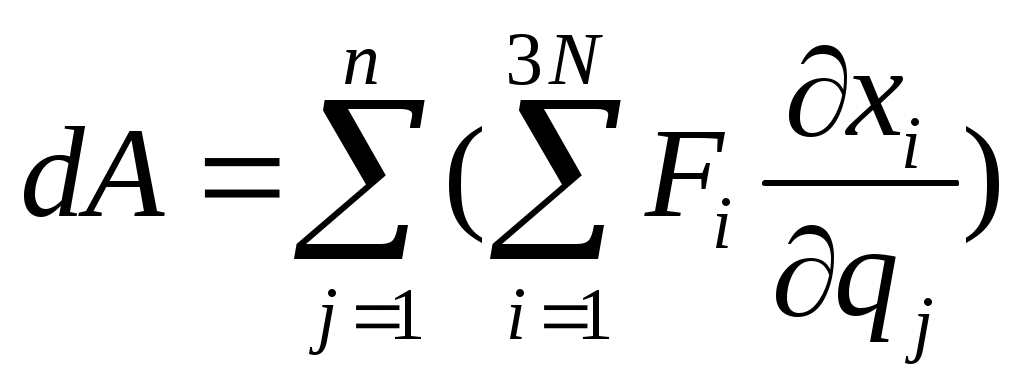 . .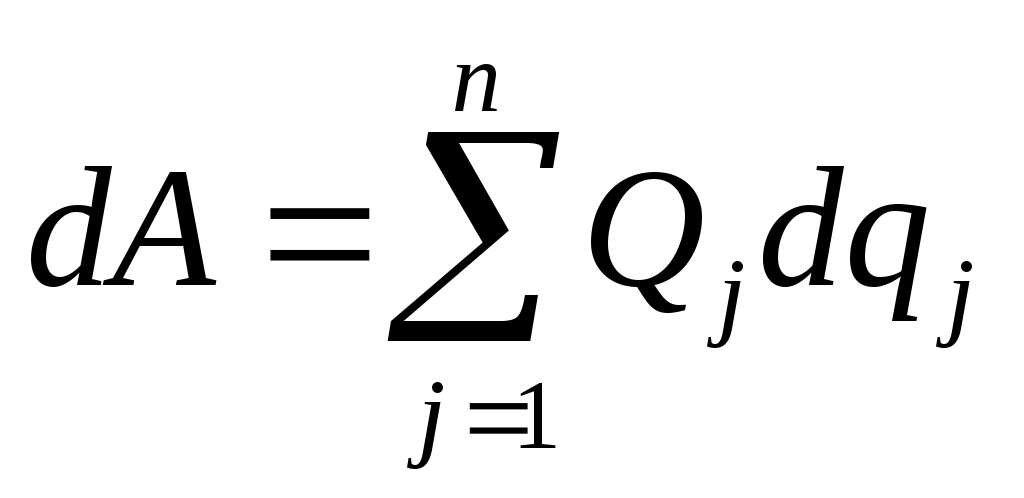
где 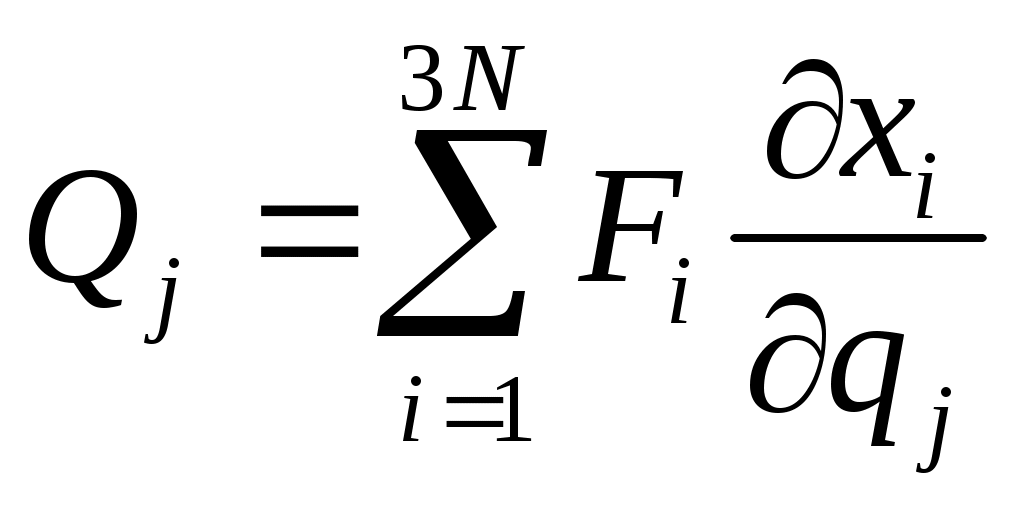 обобщенная сила. каждой ОК соответствует свой ОС. обобщенная сила. каждой ОК соответствует свой ОС. 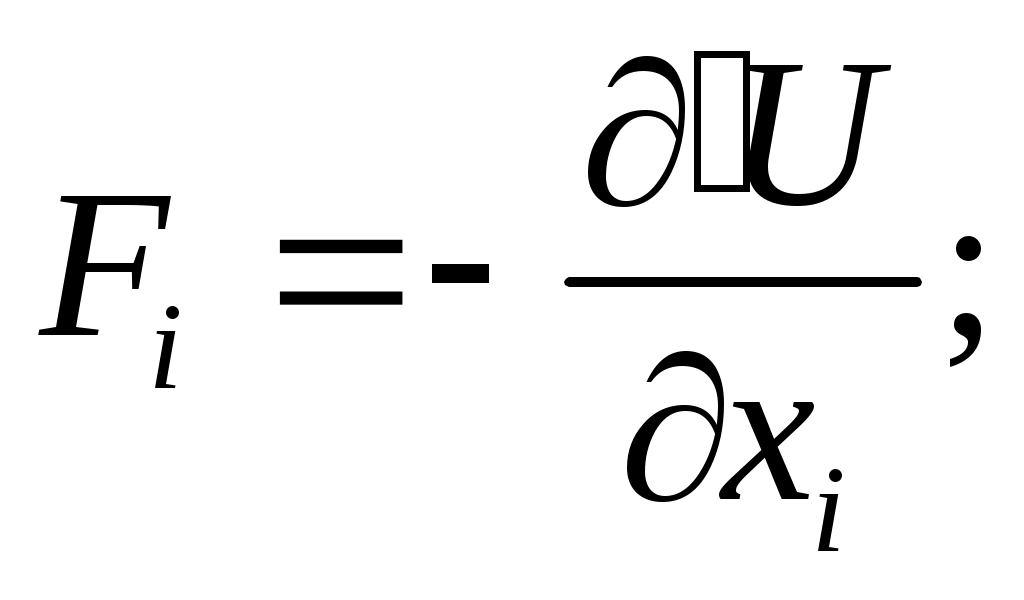 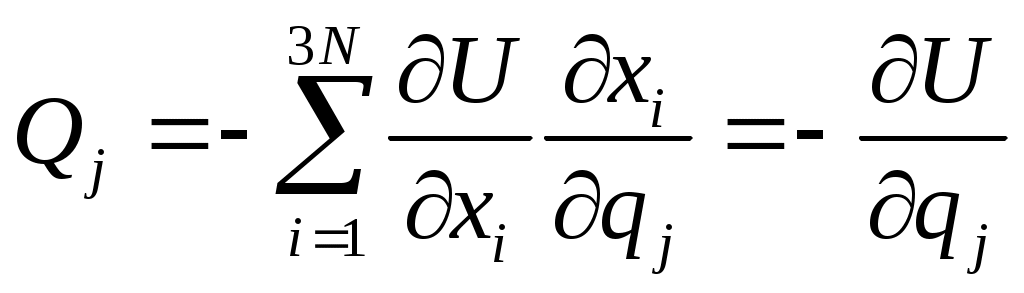
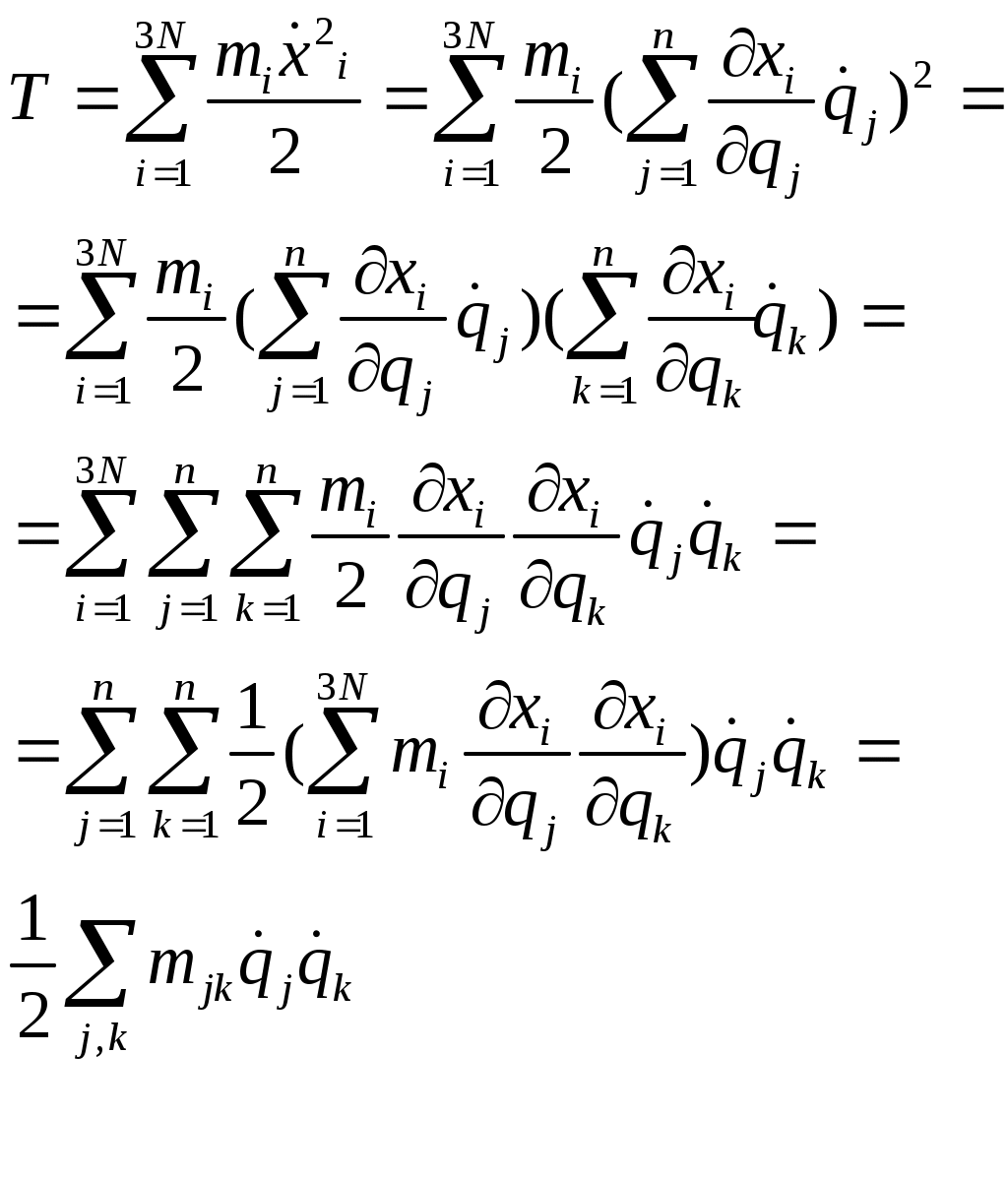
3.4. Общая ф-я теории рассеяния.
Получим общую формулу, завис. от предельного параметра и угла. b=b(θ). N(>θ)=N(b2.
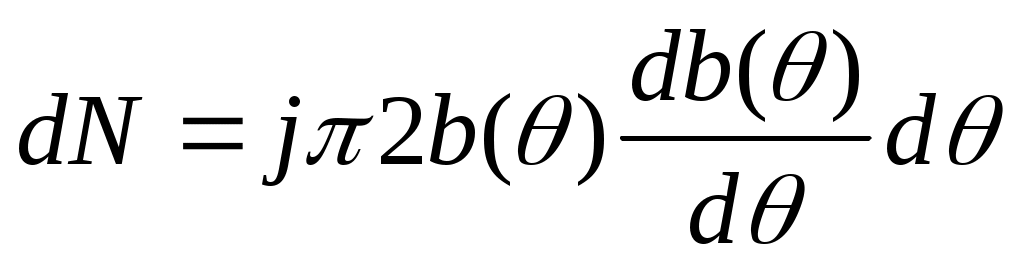 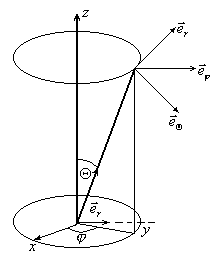 dN величина «-». Если понимать под dN число частиц dN(θ< θ’< θ+d θ) чтобы она была «+», надо dN величина «-». Если понимать под dN число частиц dN(θ< θ’< θ+d θ) чтобы она была «+», надо 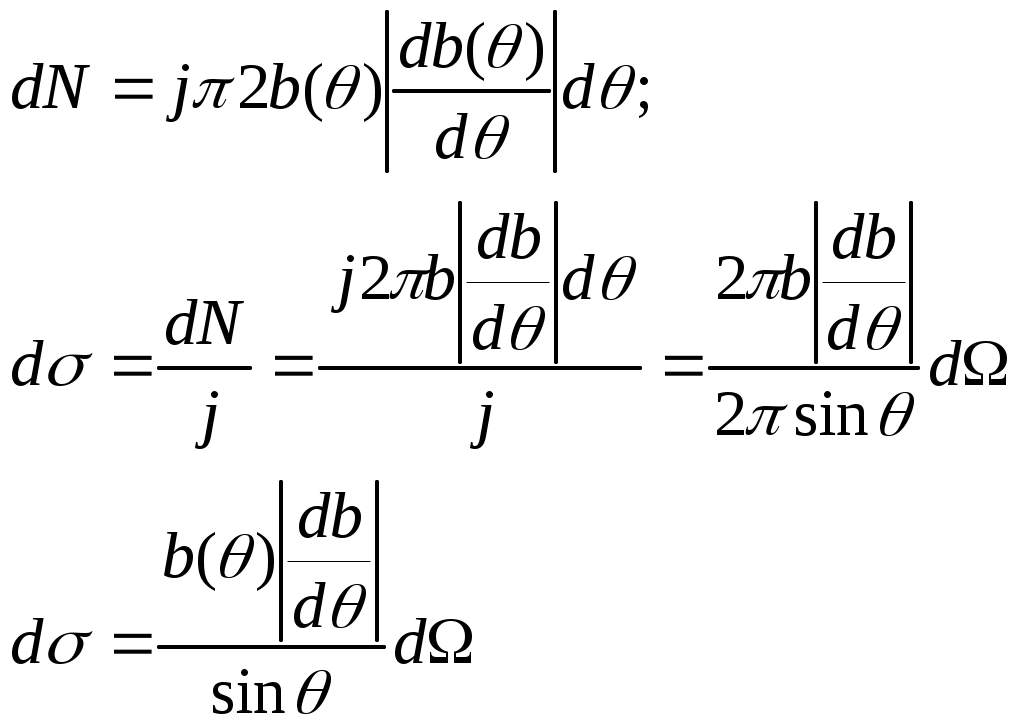
4.1.Угловая скорость.
И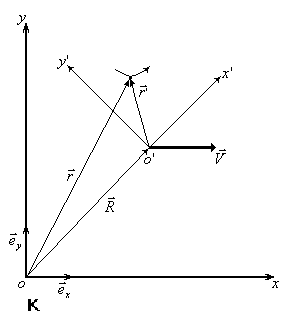 С бескон. мн-во, они движутся поступательно. Неин. сист. — вращающиеся. В ней закон Ньютона несправедлив. Чтобы был справедлив, нужно добавить силу инерции Fин. С бескон. мн-во, они движутся поступательно. Неин. сист. — вращающиеся. В ней закон Ньютона несправедлив. Чтобы был справедлив, нужно добавить силу инерции Fин. 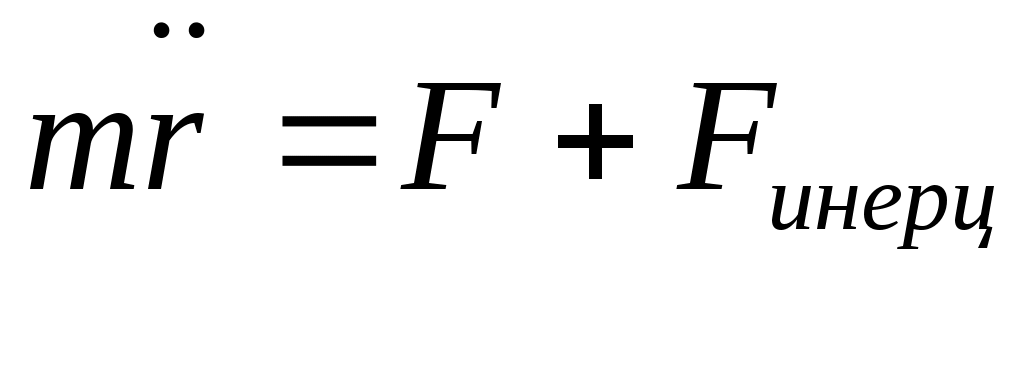
Если не изменять размер вектора, а лишь его направление, то Эл. приращение всегда перпендикулярно вектору. Введем един. вектор вдоль радиуса, то 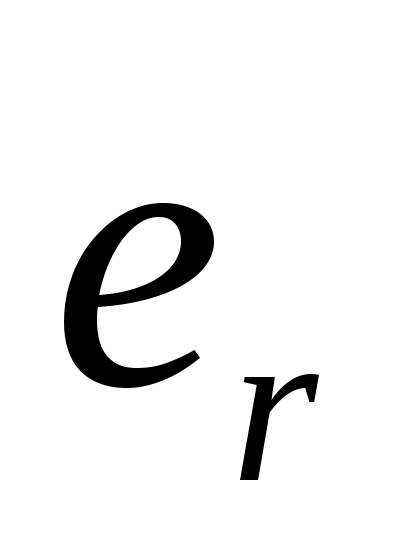 можно представить: можно представить: 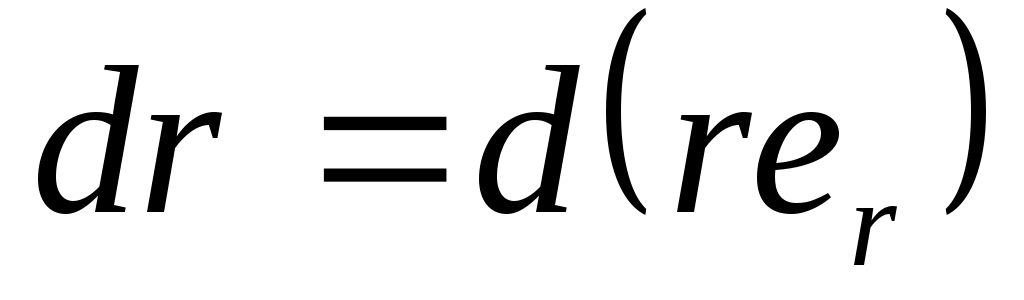 .В Декар. .В Декар.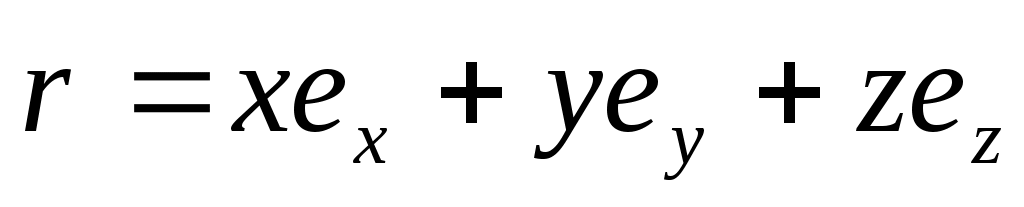
в Цилиндр.: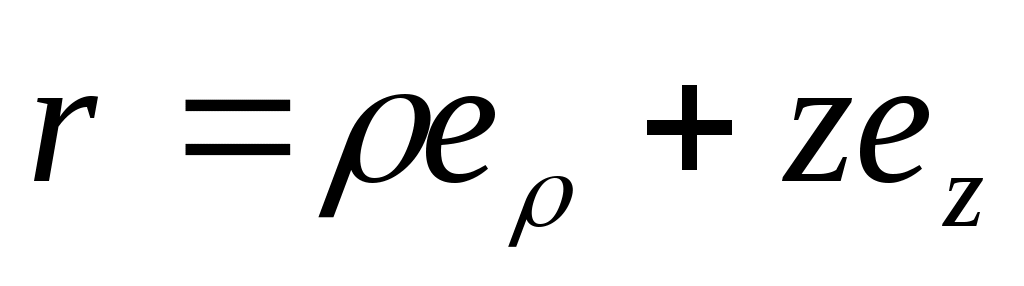
в сферич.: 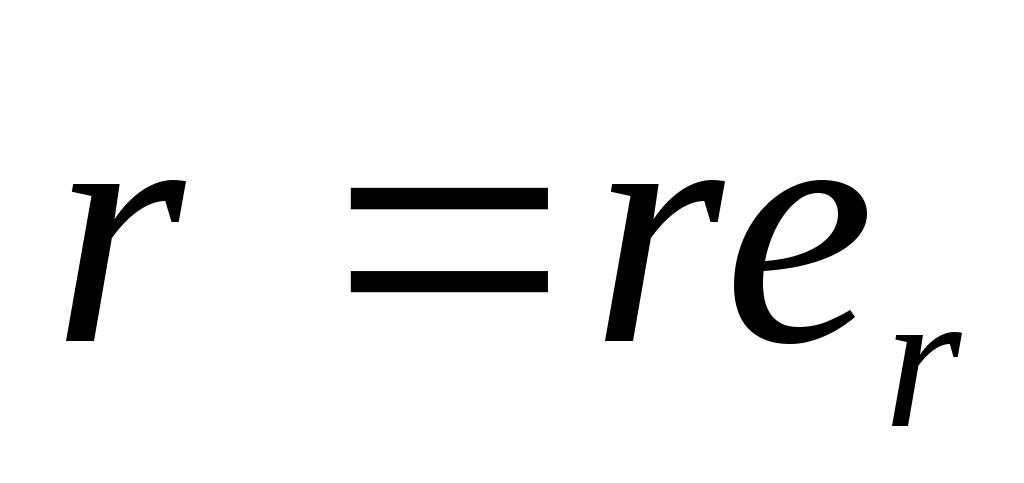
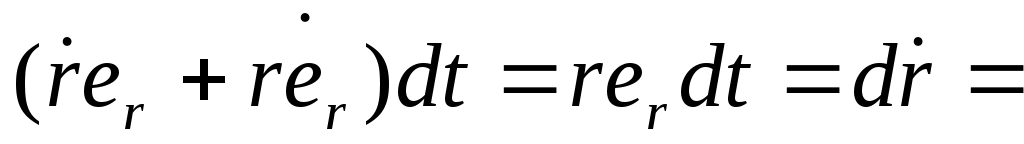 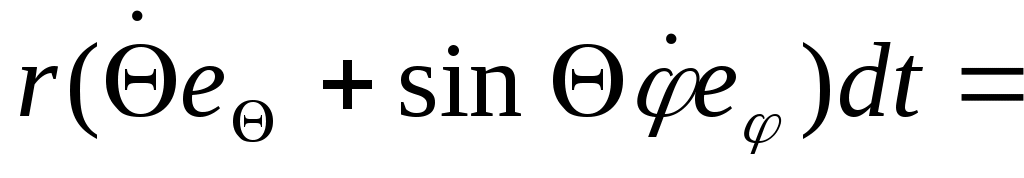 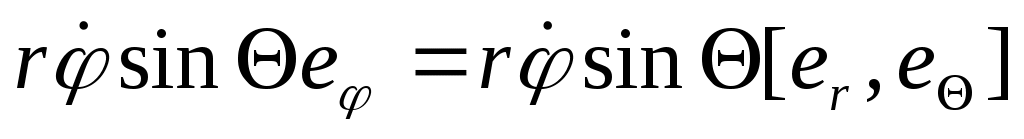 Введем Введем 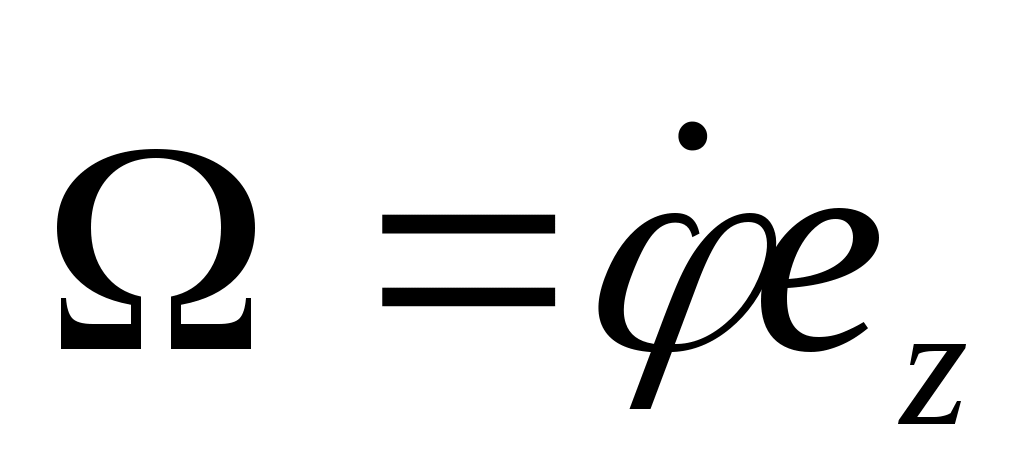 угл. ск-ть угл. ск-ть 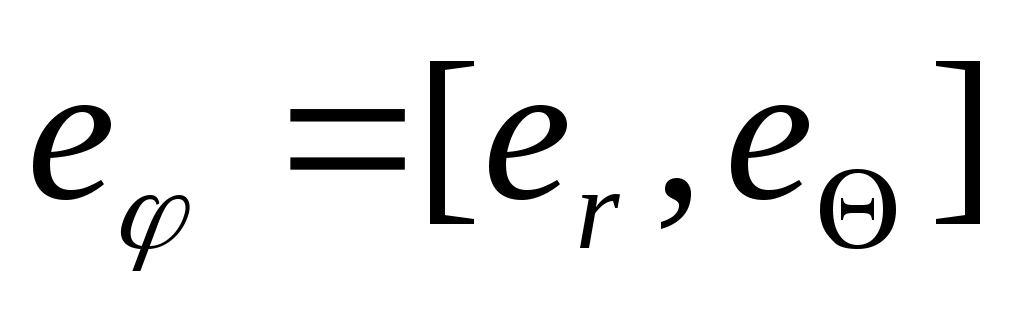 Возьмем модуль Возьмем модуль 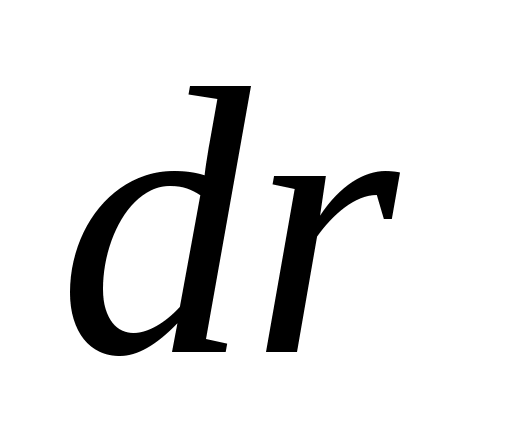
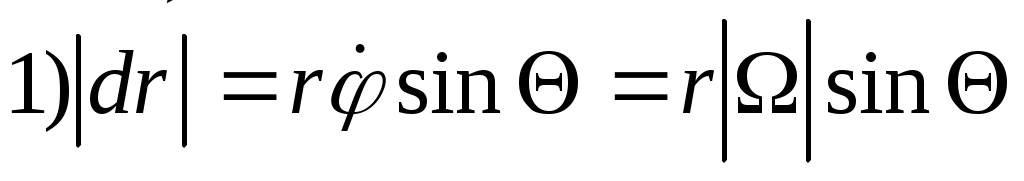
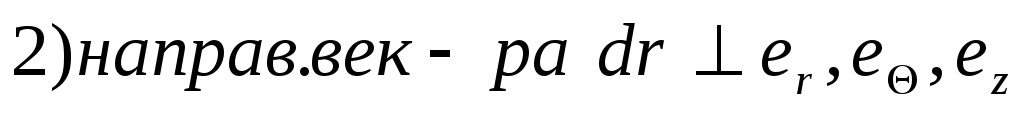
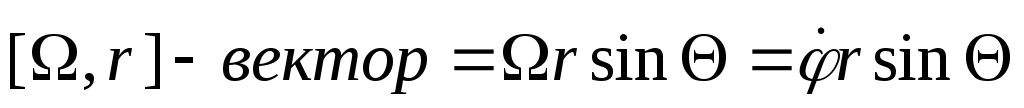 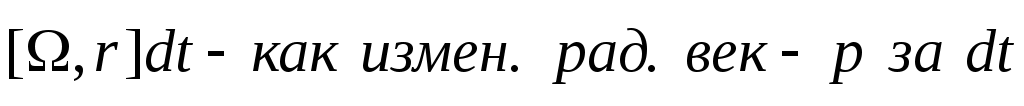 фиксир. вокруг оси фиксир. вокруг оси 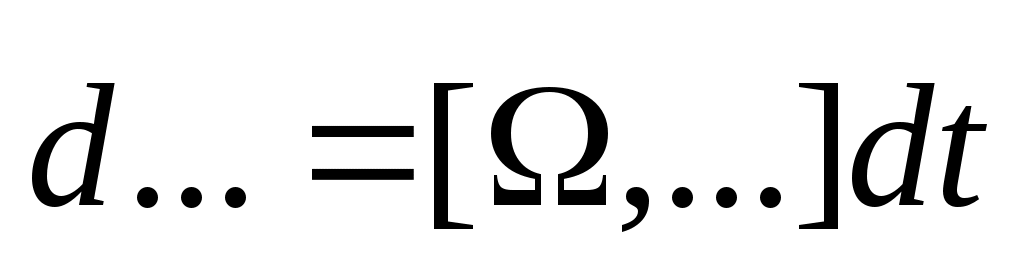
4.2. Абсолютная и относительная ск-ть.
Рассм. 2 сист. координат: неподв К и К’ (дв-ся отн-но К) R – рад.вектор означает начало штрихованной отн-но центра нештрихованной. 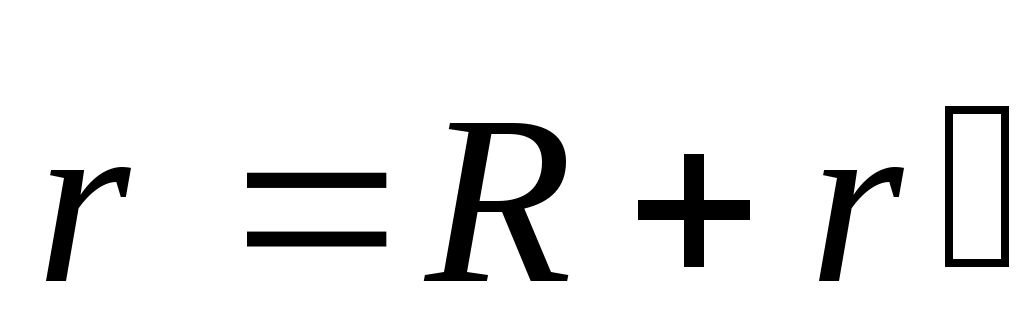
Только в случае поступательного движения.
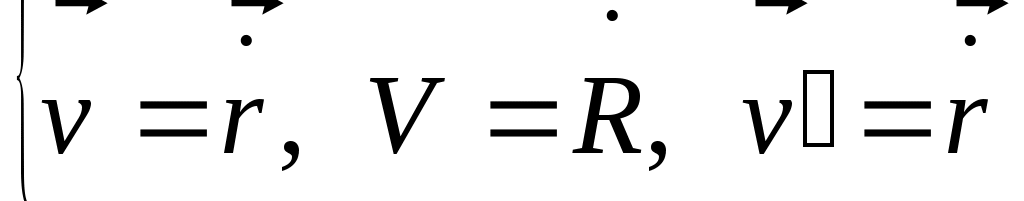 . .
если сист. к’ движ. отн. к поступат., то продиф. это равно 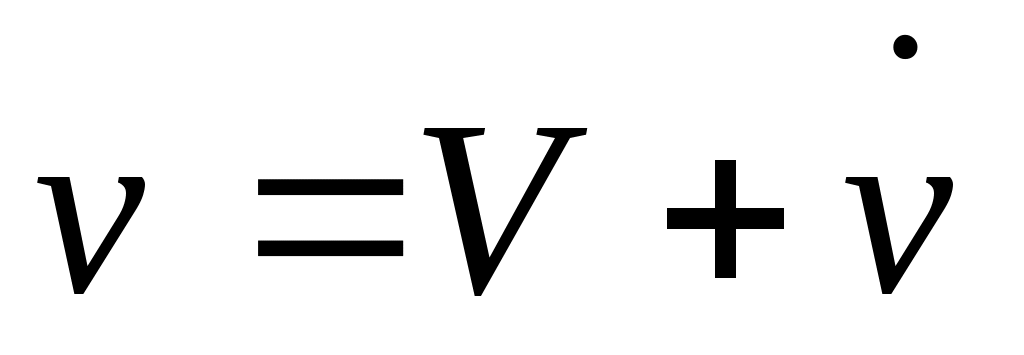 . Если нет, то: в K . . Если нет, то: в K . 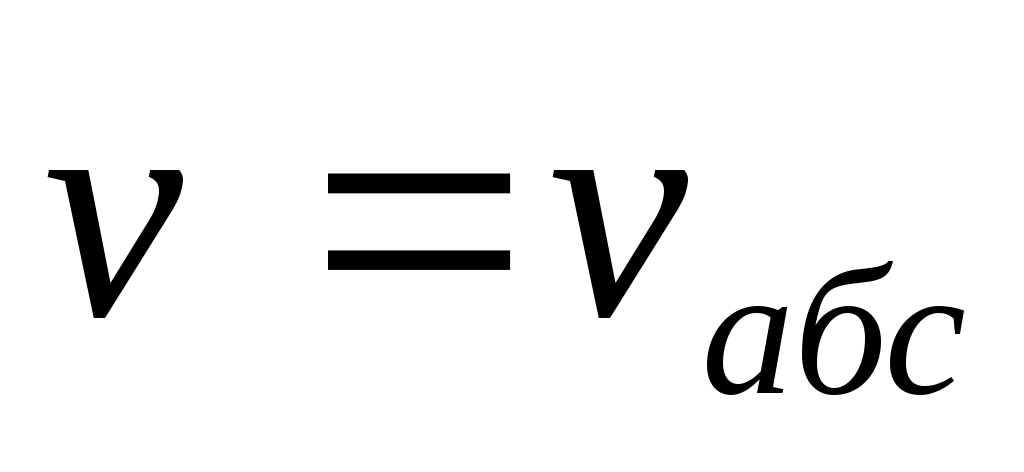 и в K’ и в K’ 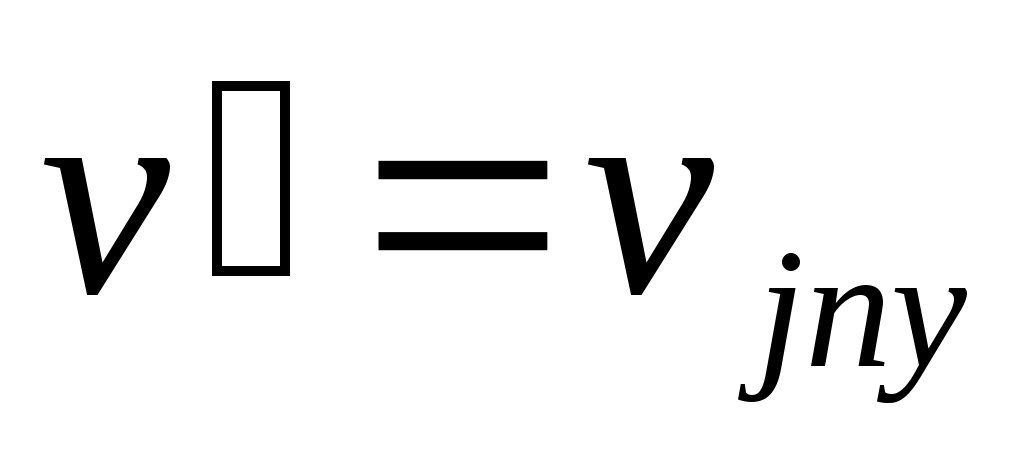 . .
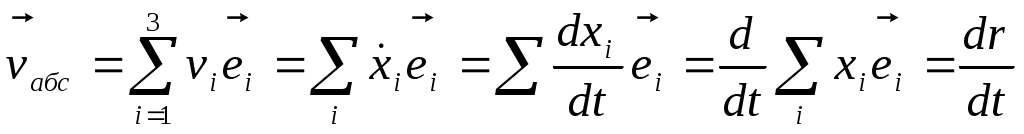
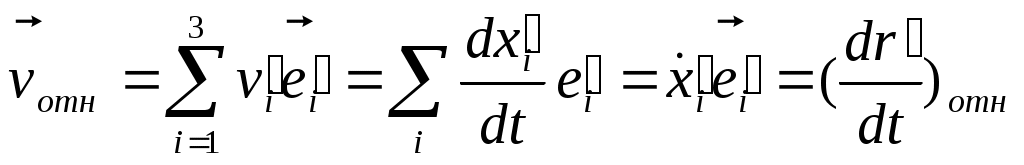 Выразим v абс. через v отн. Выразим v абс. через v отн. 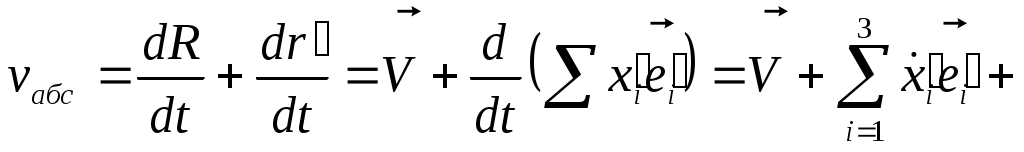 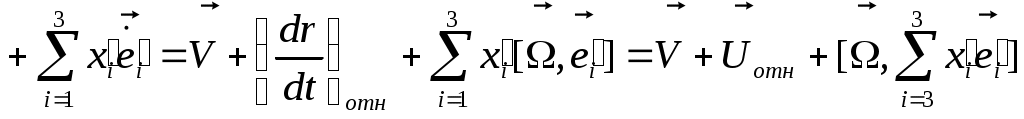 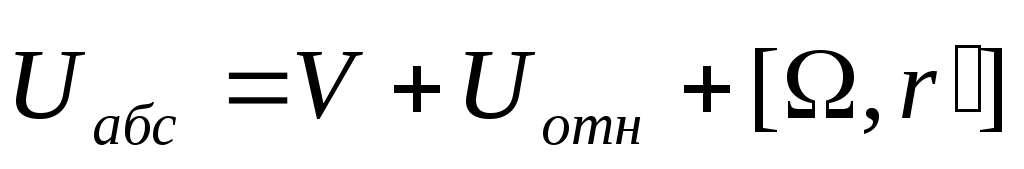 -связ. ск-ть дв-я в одн. системе с другой системой. -связ. ск-ть дв-я в одн. системе с другой системой.
4.3. Абсолютн. и относительн. ускорение.
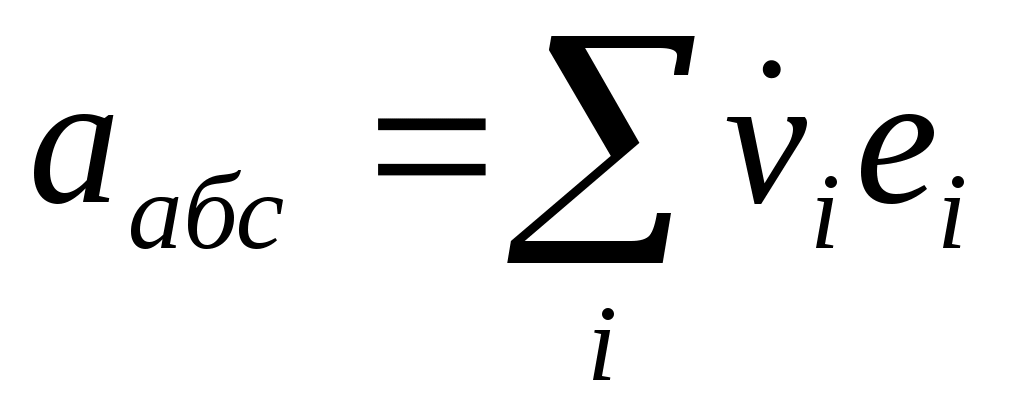 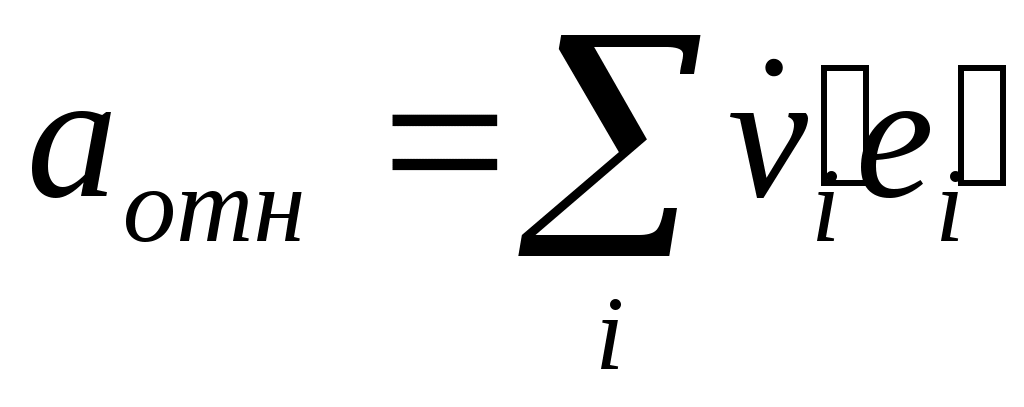
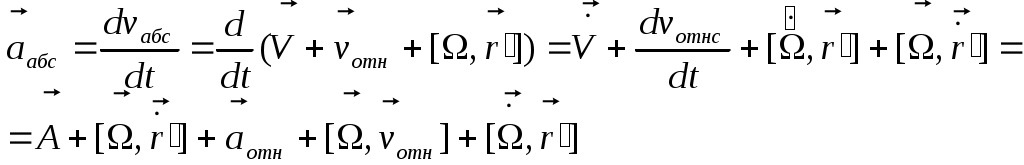
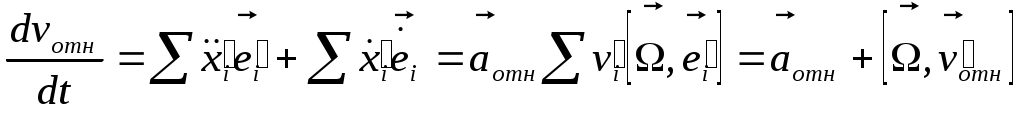
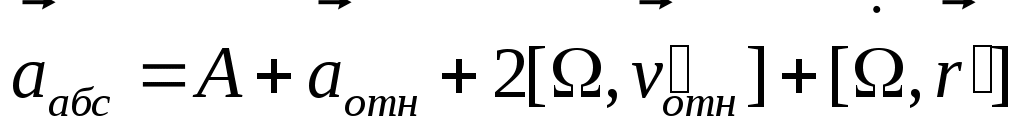
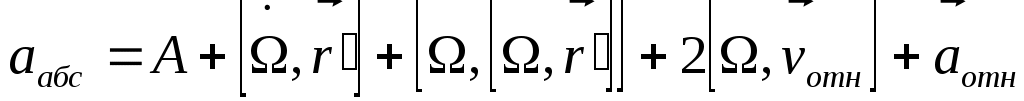
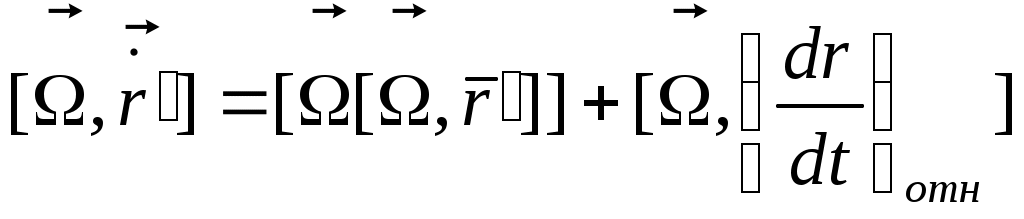 если вращ. с пост. ск-ю послед. слогаем. если вращ. с пост. ск-ю послед. слогаем.
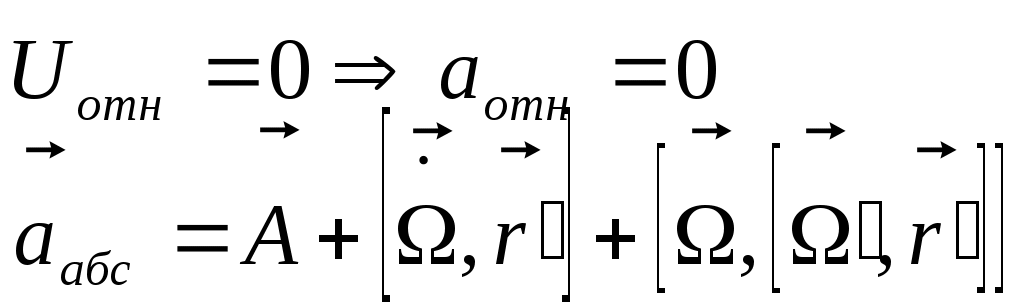
ускорение точки, которая неподвижна в K’ СК.
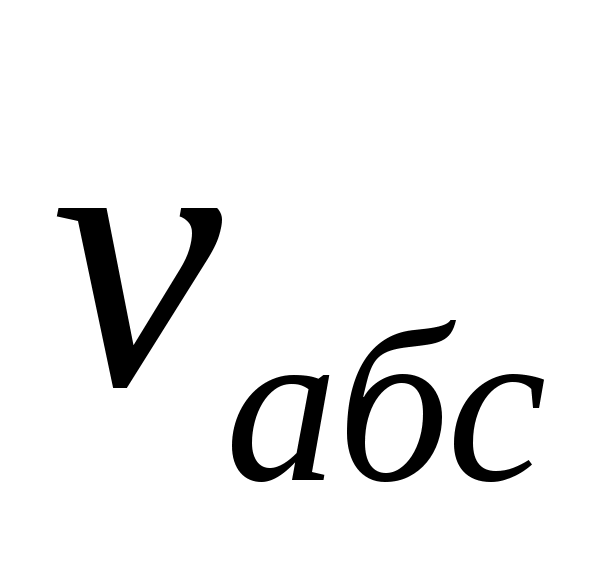 = ускорению геом. точки K’ (переносное) + = ускорению геом. точки K’ (переносное) + 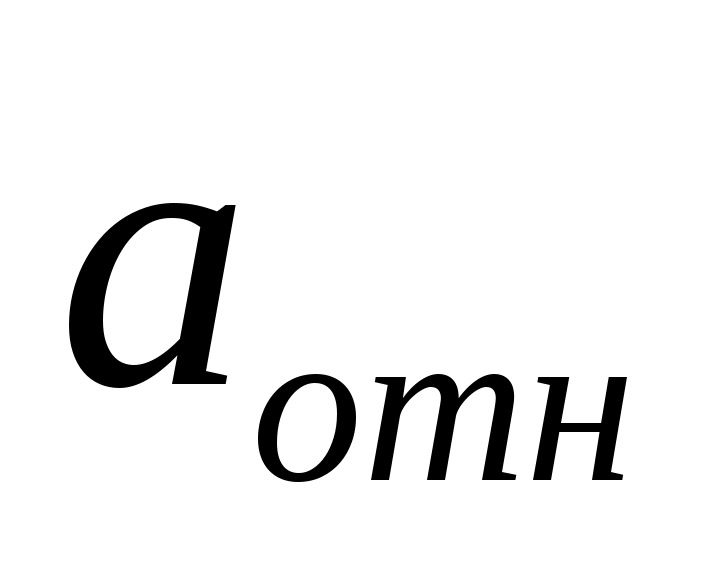 (ускоренеи ч-цы отн-но K’) + кореолисово ускорение (ускоренеи ч-цы отн-но K’) + кореолисово ускорение 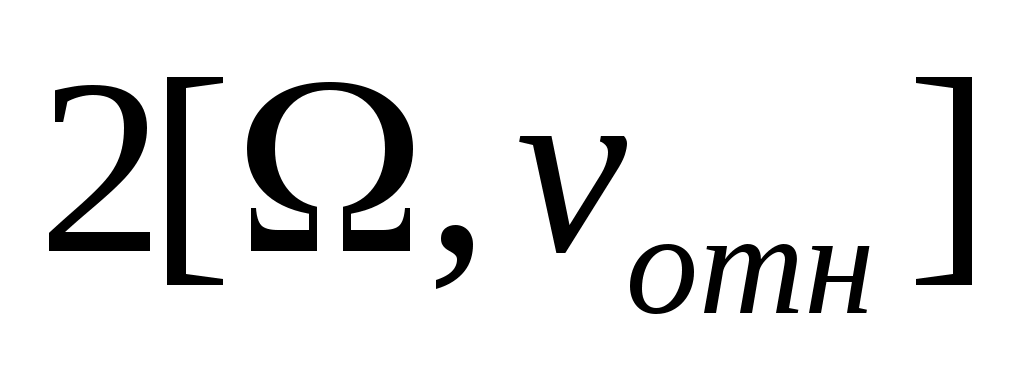
4.5. Силы инерции
В инерциальной С.О.: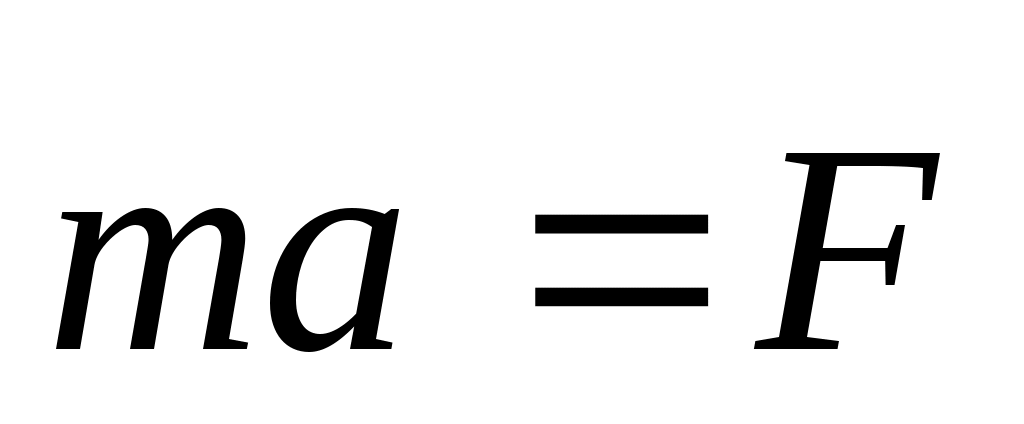 ;в неинерц.С.О.: ;в неинерц.С.О.: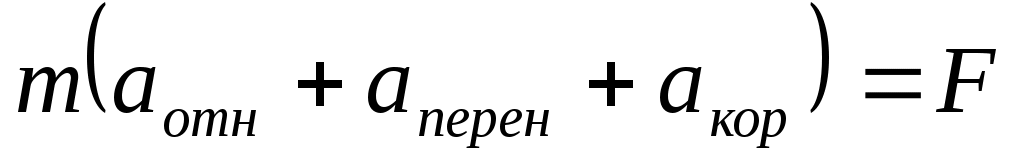
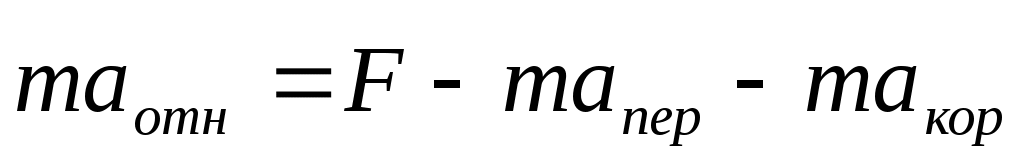 ; ; 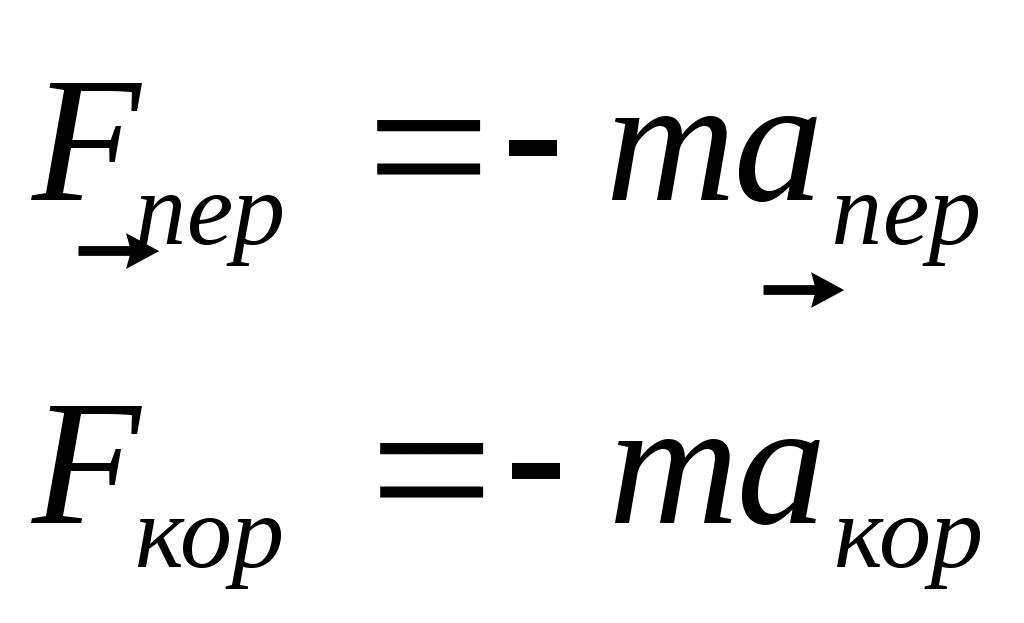 }-cилы инерции (*) }-cилы инерции (*)
Если предположить, что в любой СК F=ma, то если определять F только в ИСК, то надо добавить (*).
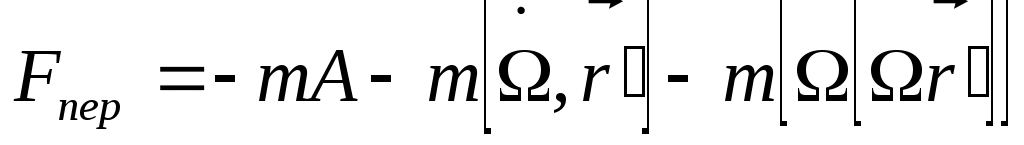 ; если начало координат общих систем совп., а скорость является постоянной величиной, то ; если начало координат общих систем совп., а скорость является постоянной величиной, то
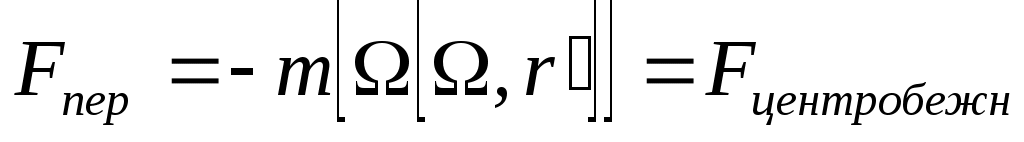 ; ; 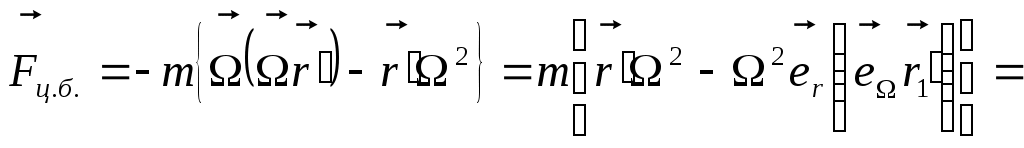 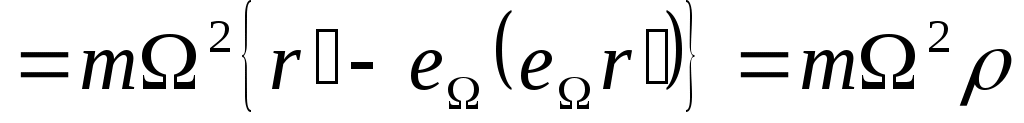
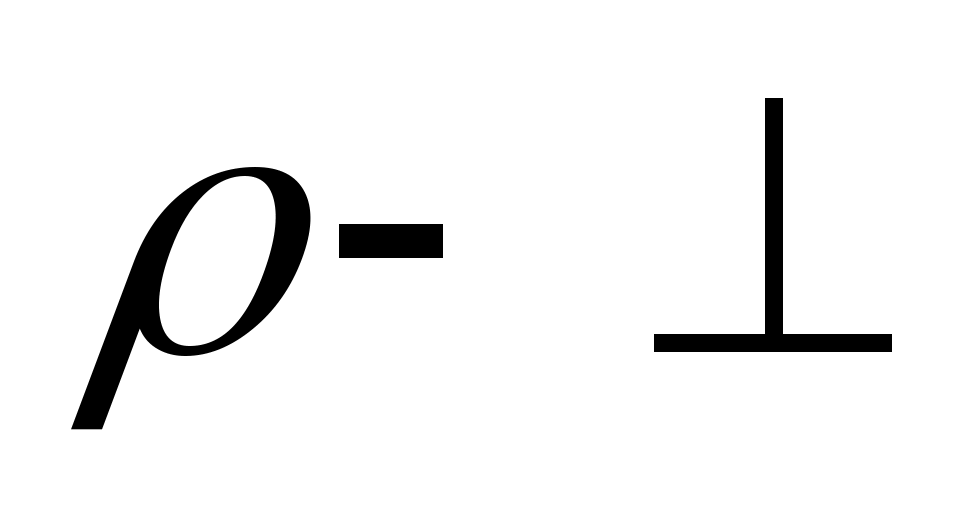 оси вр. и напр. от нее оси вр. и напр. от нее
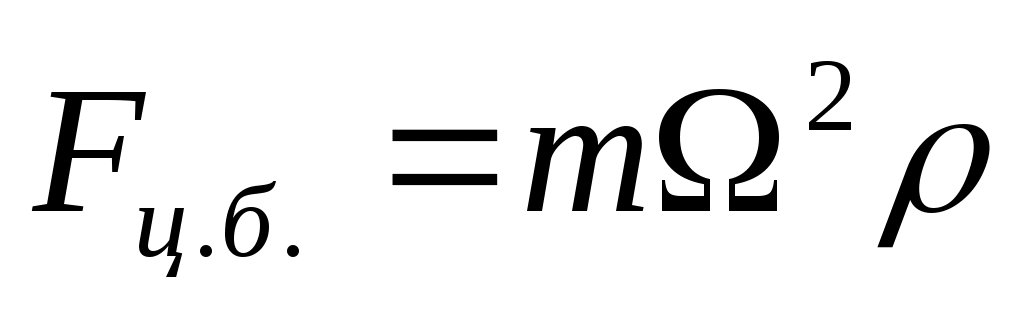
5.1. Импульс системы.
Система — конечная или бесконечная совокупность мат. точек, взаимодействующих м\д собой. 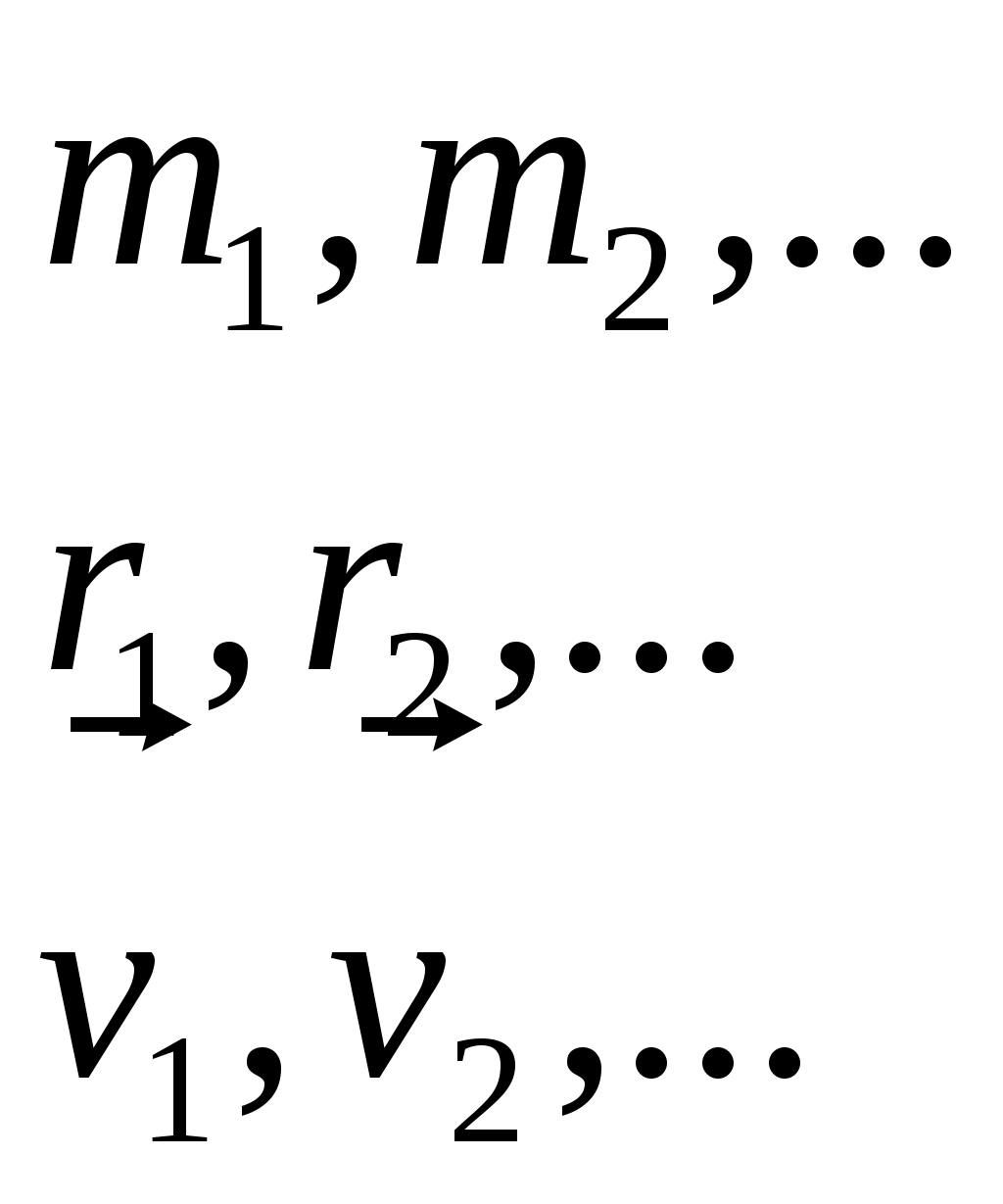 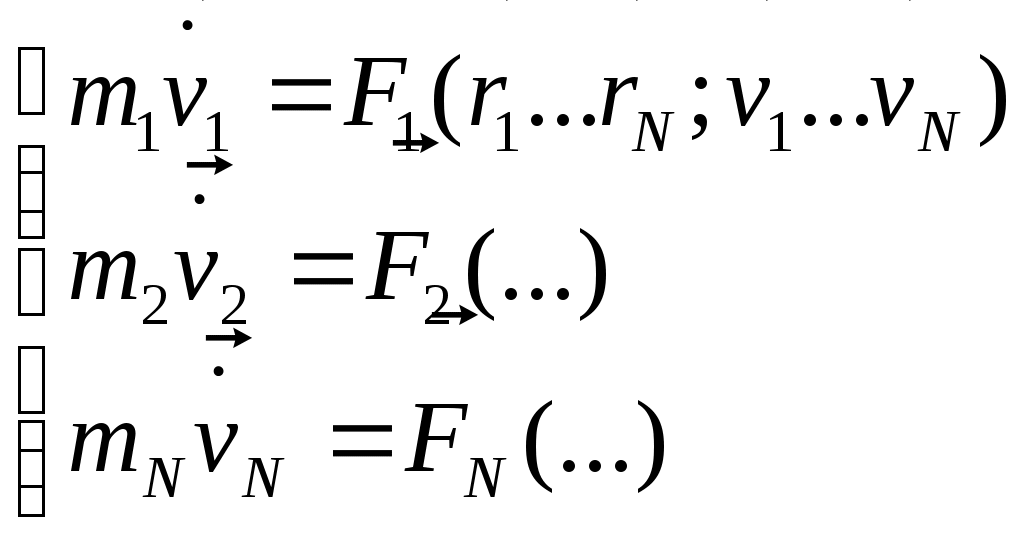 В общем случае. Fi= В общем случае. Fi=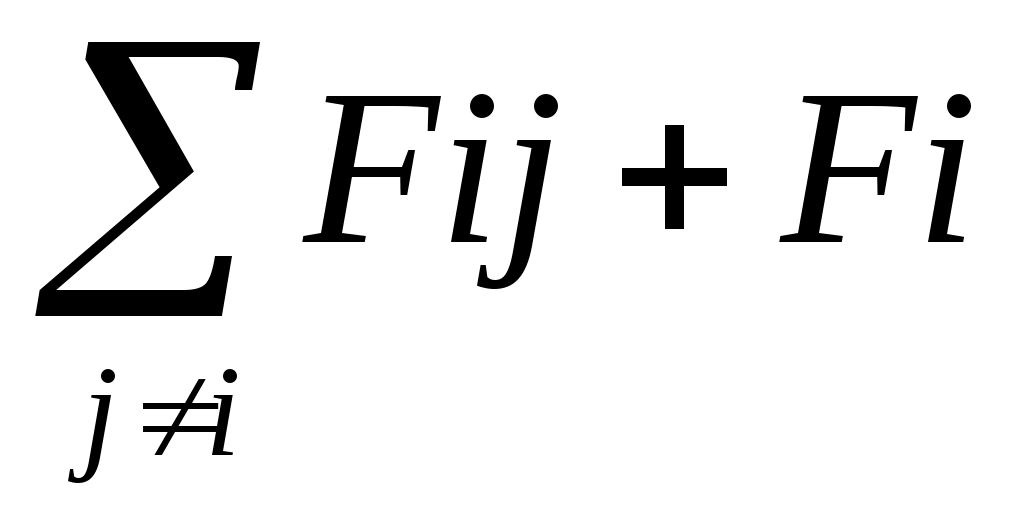 внешн Fij – сила со стороны j частицы на i частицу. m1v1=F12+F13+…+F1N+F1внешн внешн Fij – сила со стороны j частицы на i частицу. m1v1=F12+F13+…+F1N+F1внешн
…
mNvN=FN1+FN2+…+FN,N-1+F1внешн
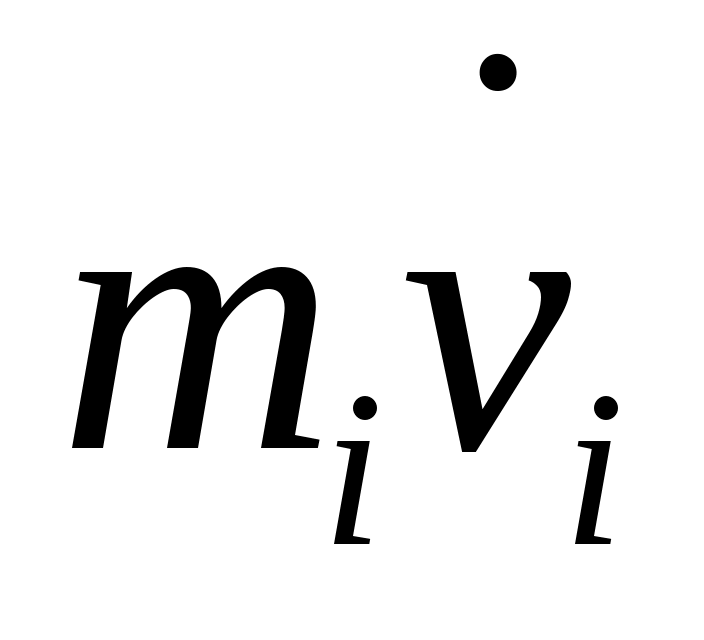 = =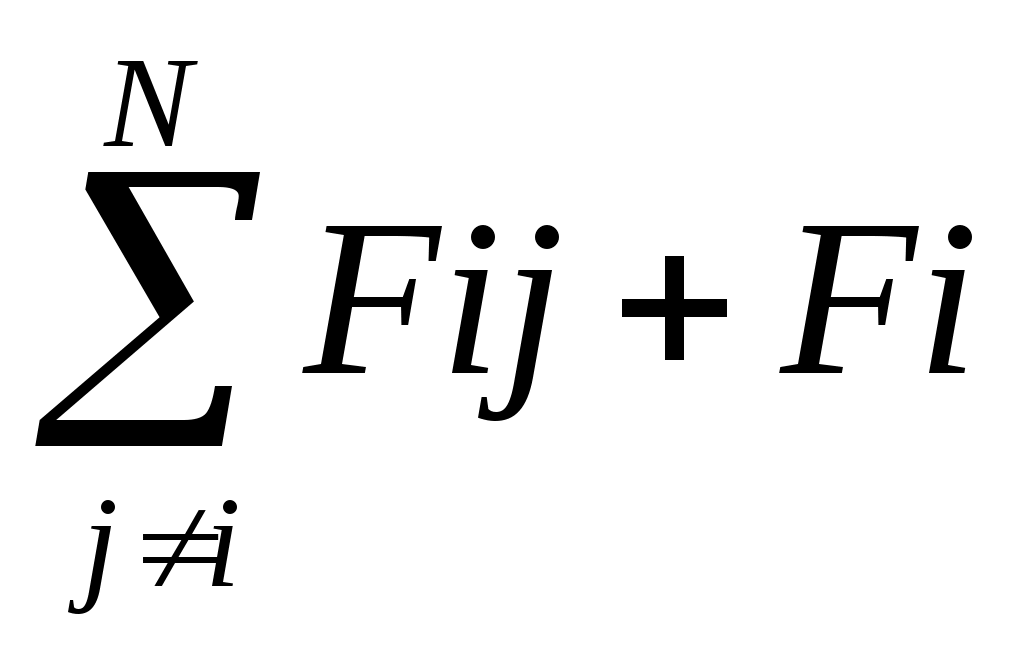 внешн ,i=1,2,…,N внешн ,i=1,2,…,N
Просуммируем это выражение по всем i:
Лев. часть: 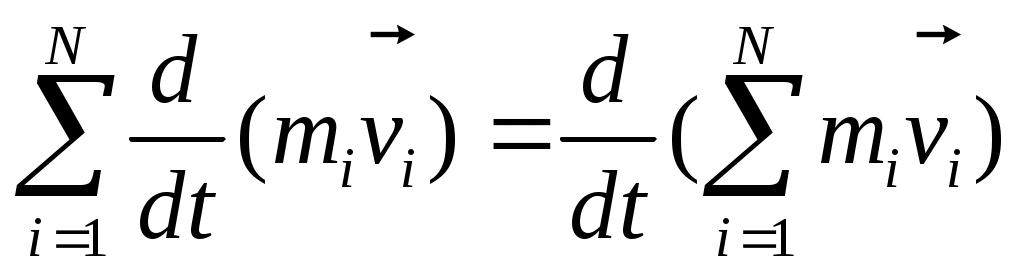
Прав. часть: 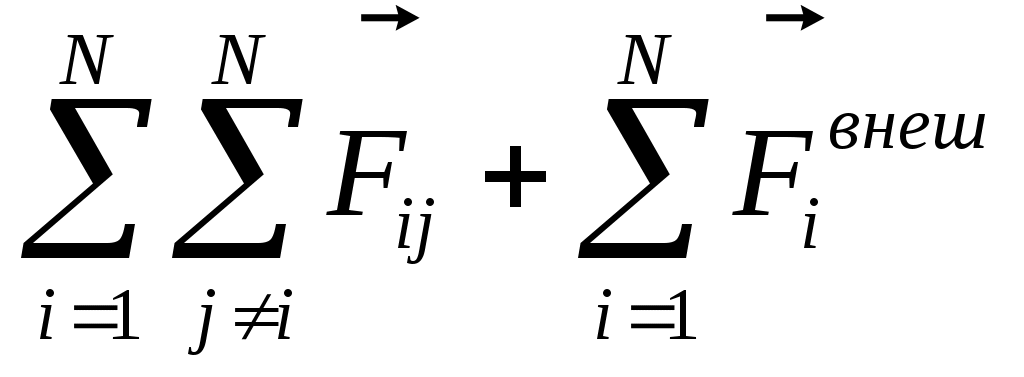
N=2: 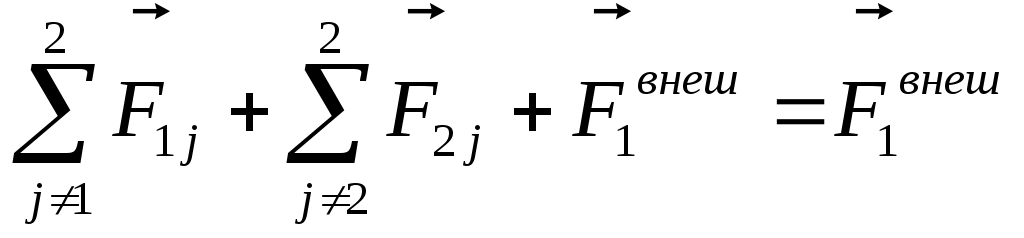
Такой же результат будет при любом N. Тогда:
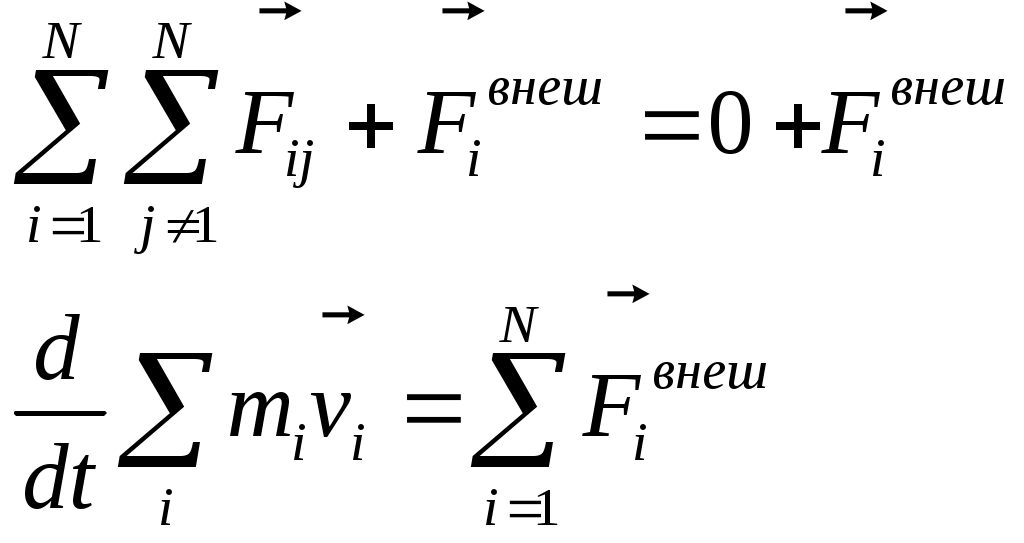 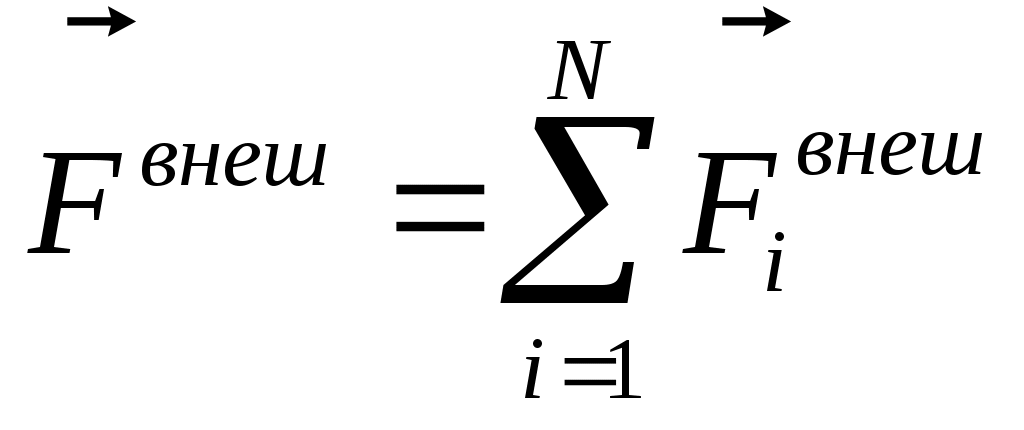 — главный вектор внешних (*) сил. Если он равен 0, то — главный вектор внешних (*) сил. Если он равен 0, то 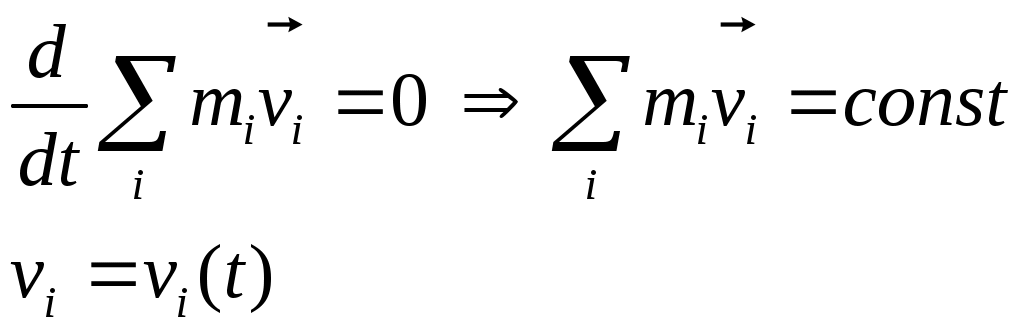 Скорость каждой частицы зависит от времени, но (*), то Скорость каждой частицы зависит от времени, но (*), то 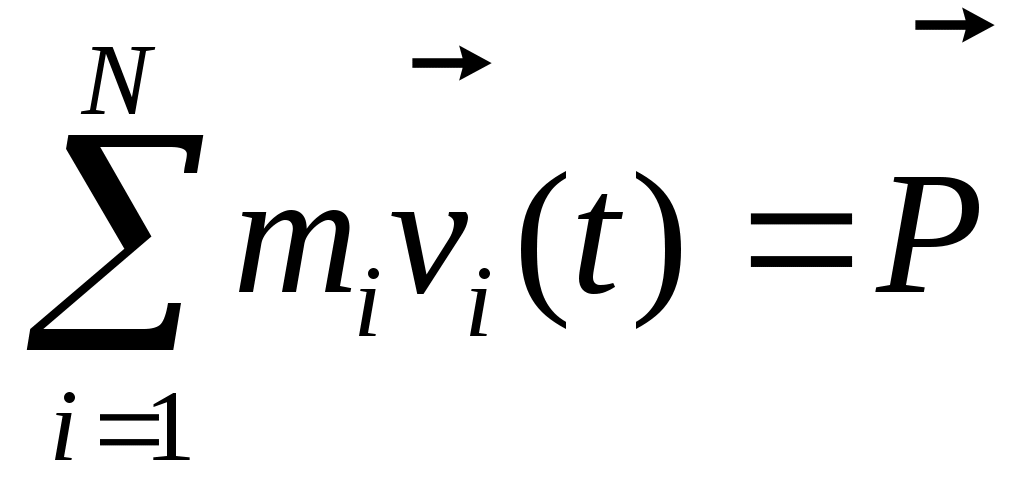 импульс системы. импульс системы. 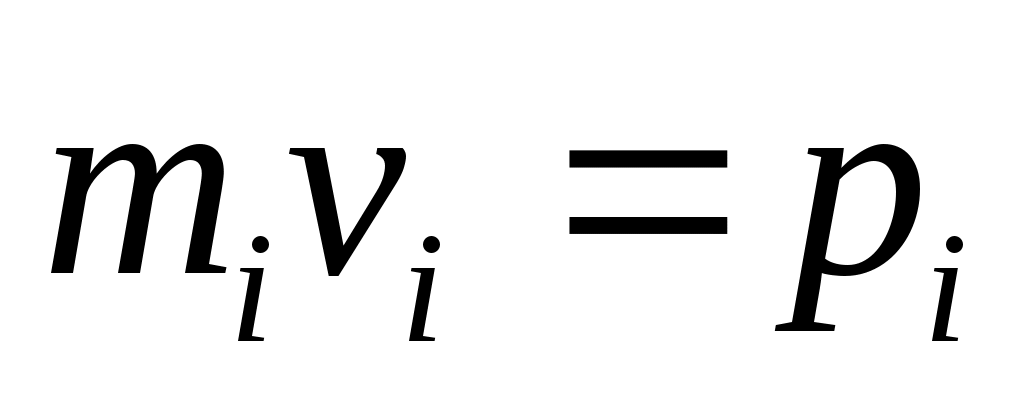 импульс i частицы. импульс i частицы. 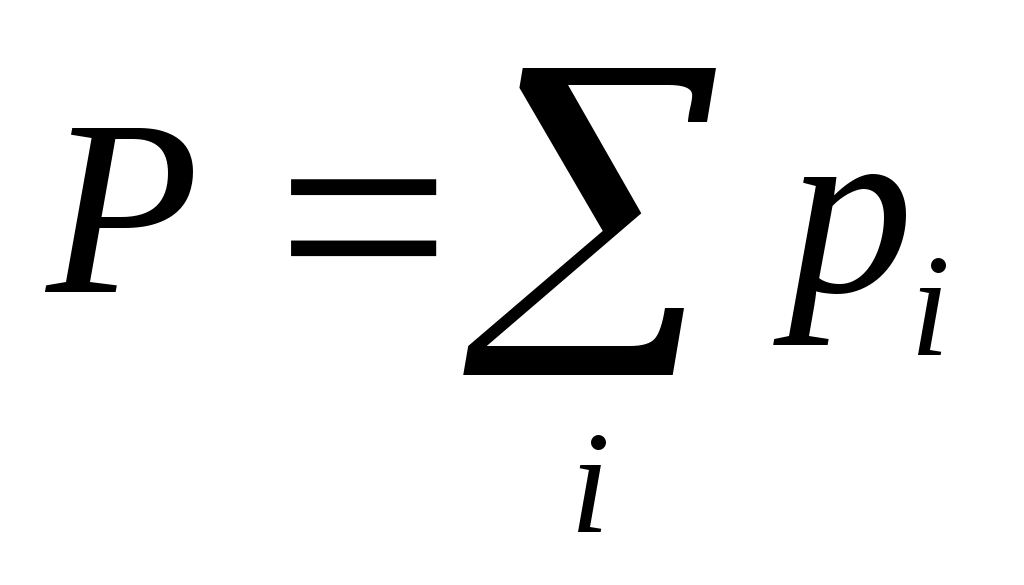 - закон сохранения импульса: если главный вектор внешних сил = 0, то импульс системы const. Или Если x-проекция Fx внеш = 0, то соответствующая проекция Px=const. Если главный вектор внеш. сил не равен 0, то - закон сохранения импульса: если главный вектор внешних сил = 0, то импульс системы const. Или Если x-проекция Fx внеш = 0, то соответствующая проекция Px=const. Если главный вектор внеш. сил не равен 0, то 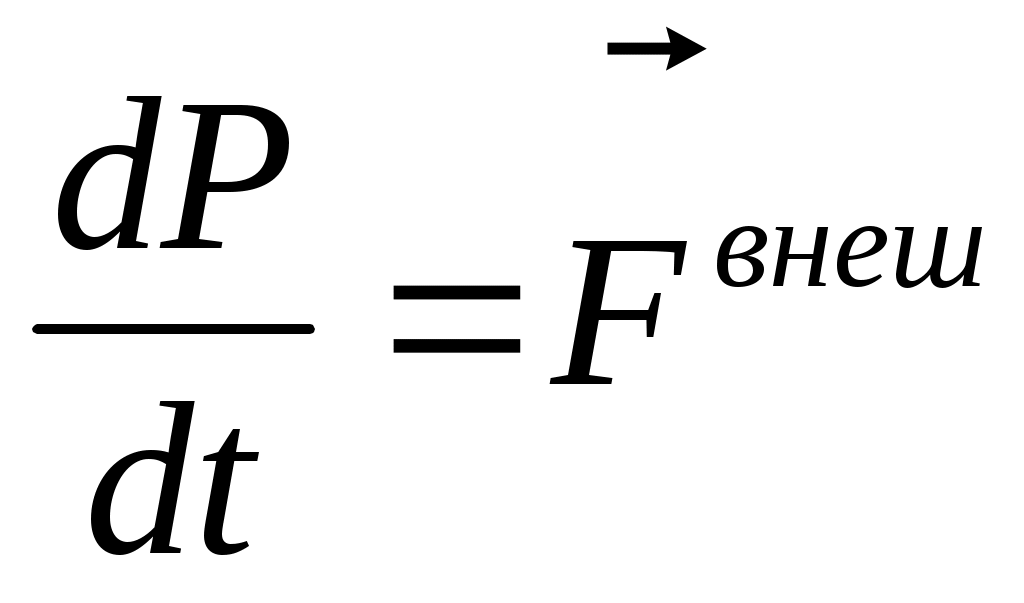 - закон изменения импульса системы. - закон изменения импульса системы.
5.2. Момент импульса системы.
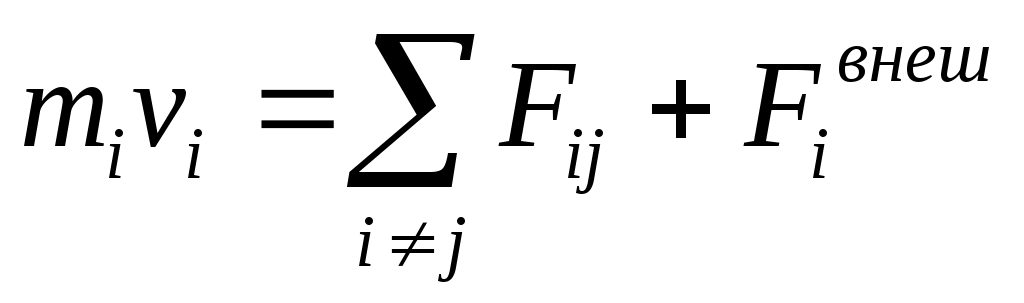 Умножим векторно обе части на Умножим векторно обе части на 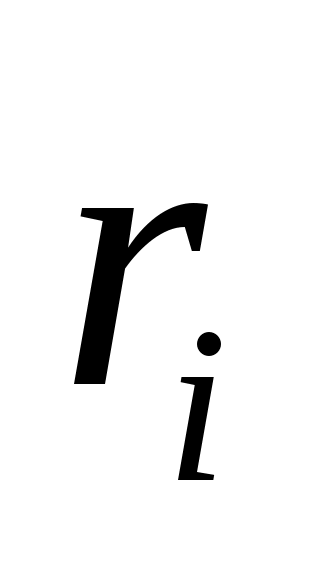 и после этого сложим: и после этого сложим:
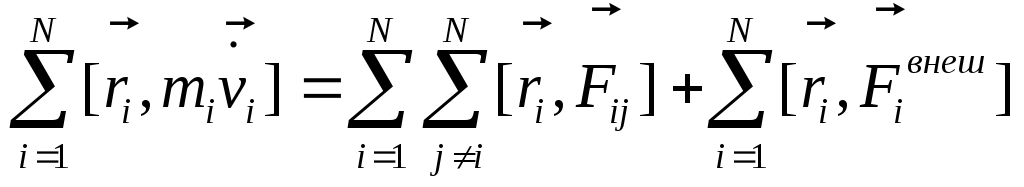 Найдем величину: Найдем величину: 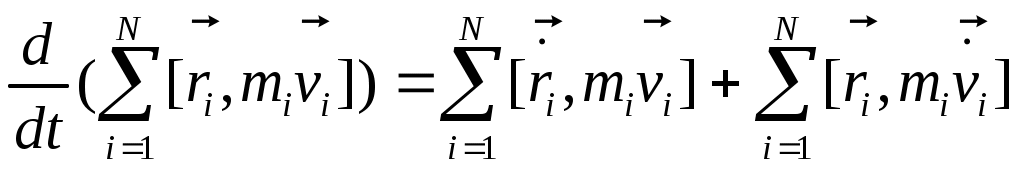 Правая часть: N=2 Правая часть: N=2
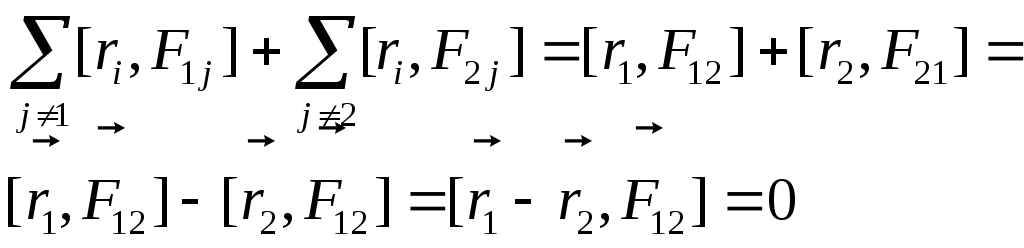 (для центральных сил). Если силы центральные, то сила взаимодействия лежит на одной прямой с вектором (для центральных сил). Если силы центральные, то сила взаимодействия лежит на одной прямой с вектором 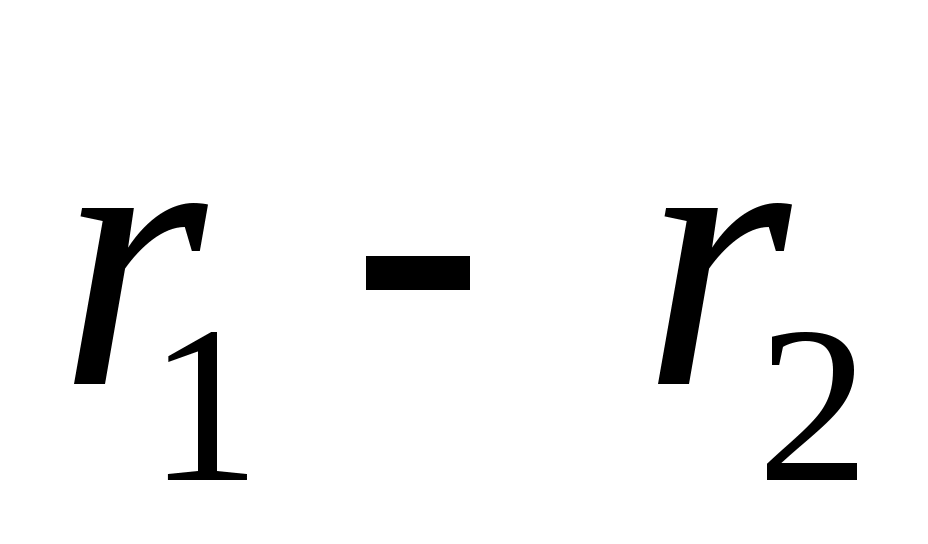 . т.е. вектор и F12 коллинеарны. . т.е. вектор и F12 коллинеарны. 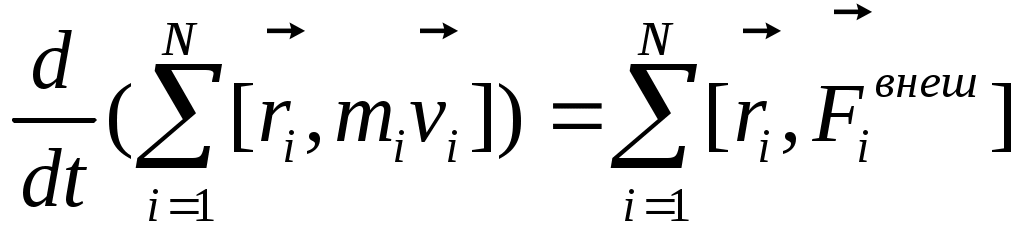
|
|
|
 Скачать 1.66 Mb.
Скачать 1.66 Mb.
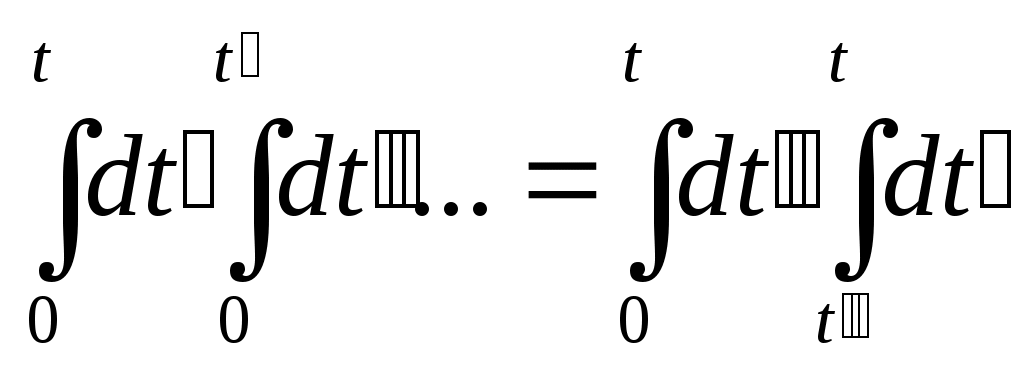 — правило Дирихле. Применяя его к (*), получим:
— правило Дирихле. Применяя его к (*), получим: 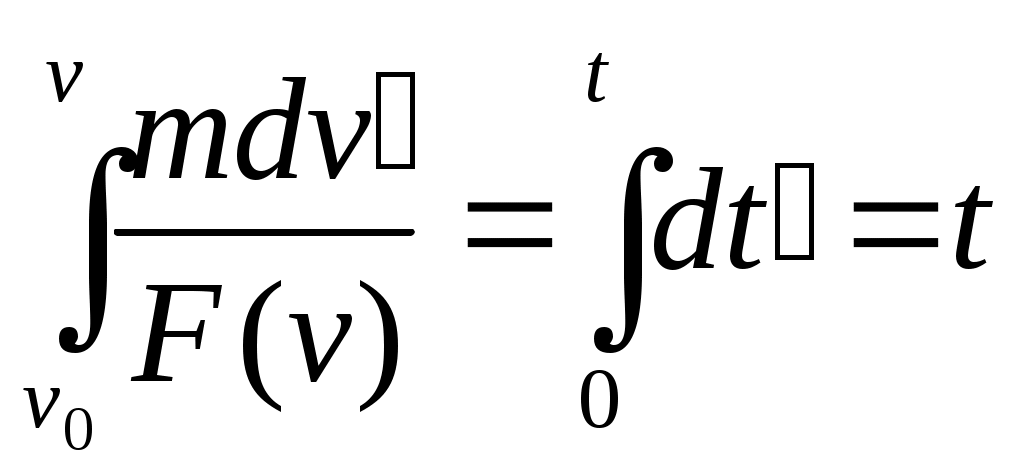 Получаем решение в виде:
Получаем решение в виде: 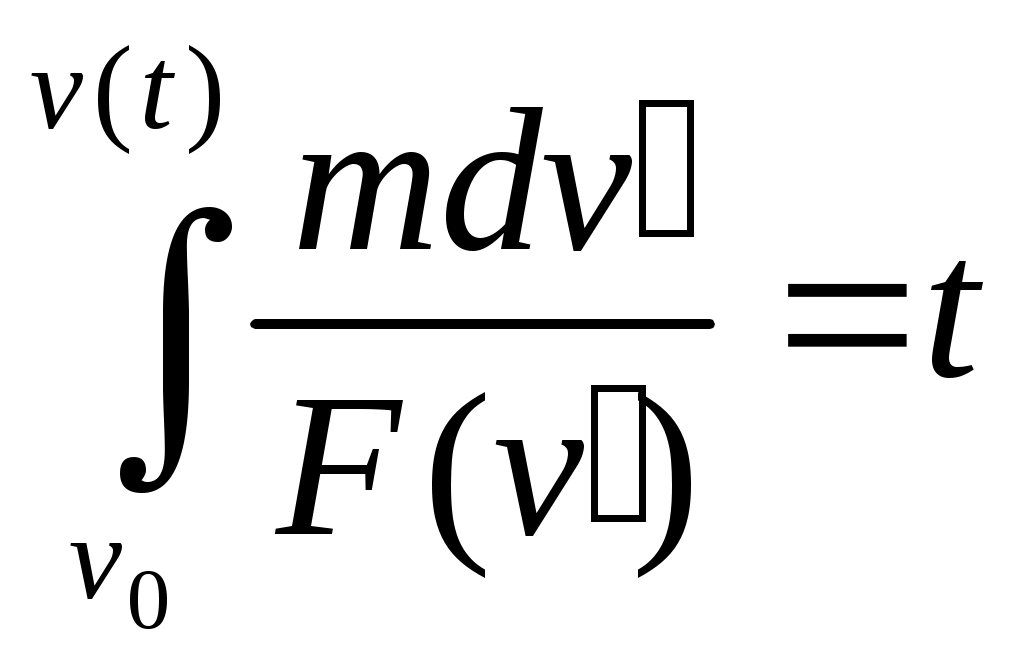 здесь t=f(v) — некот. ф-я от верхнего предела. А надо найти v как ф-ю от t. Это делается переходом к обр. ф-ии v = f-1(t). v=dx/dt. dx/dt=f-1(t)
здесь t=f(v) — некот. ф-я от верхнего предела. А надо найти v как ф-ю от t. Это делается переходом к обр. ф-ии v = f-1(t). v=dx/dt. dx/dt=f-1(t)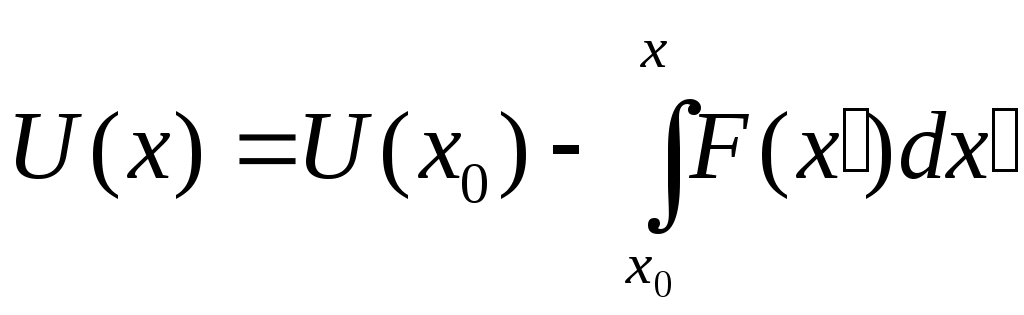 Эта ф-я наз-ся потенц. энергией.
Эта ф-я наз-ся потенц. энергией. 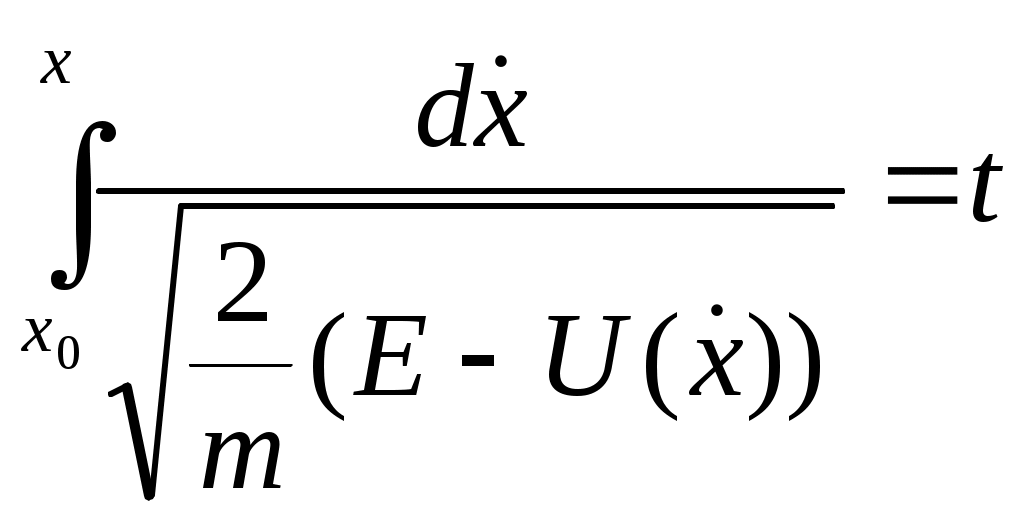 . Получили зависимость t от x. Найдем обратную ф-ю x = f-1(t)— это и есть решение задачи. Отметим св-ва корня. Е-U: кинет. энергия mv2/2. Массу сократили, осталось v2 извлекли корень, получили v. По определению скорости dx=vdt. Корень — абс. величина ск-ти, заданная как ф-я координаты. Знак + или – определяет направление движения.
. Получили зависимость t от x. Найдем обратную ф-ю x = f-1(t)— это и есть решение задачи. Отметим св-ва корня. Е-U: кинет. энергия mv2/2. Массу сократили, осталось v2 извлекли корень, получили v. По определению скорости dx=vdt. Корень — абс. величина ск-ти, заданная как ф-я координаты. Знак + или – определяет направление движения.
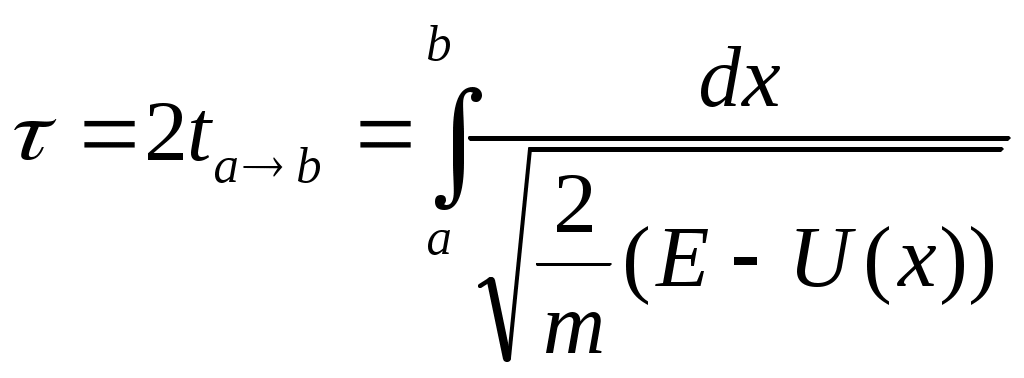 Из (*) найдем dt.
Из (*) найдем dt. 1 k k — пружина. Пусть
1 k k — пружина. Пусть 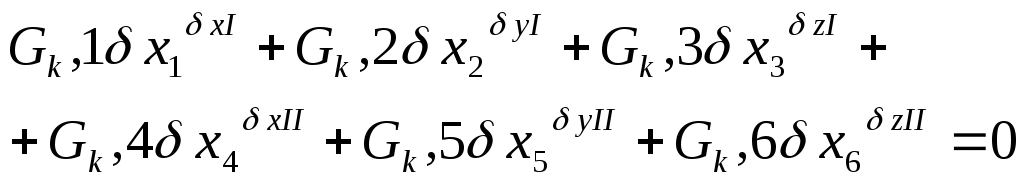
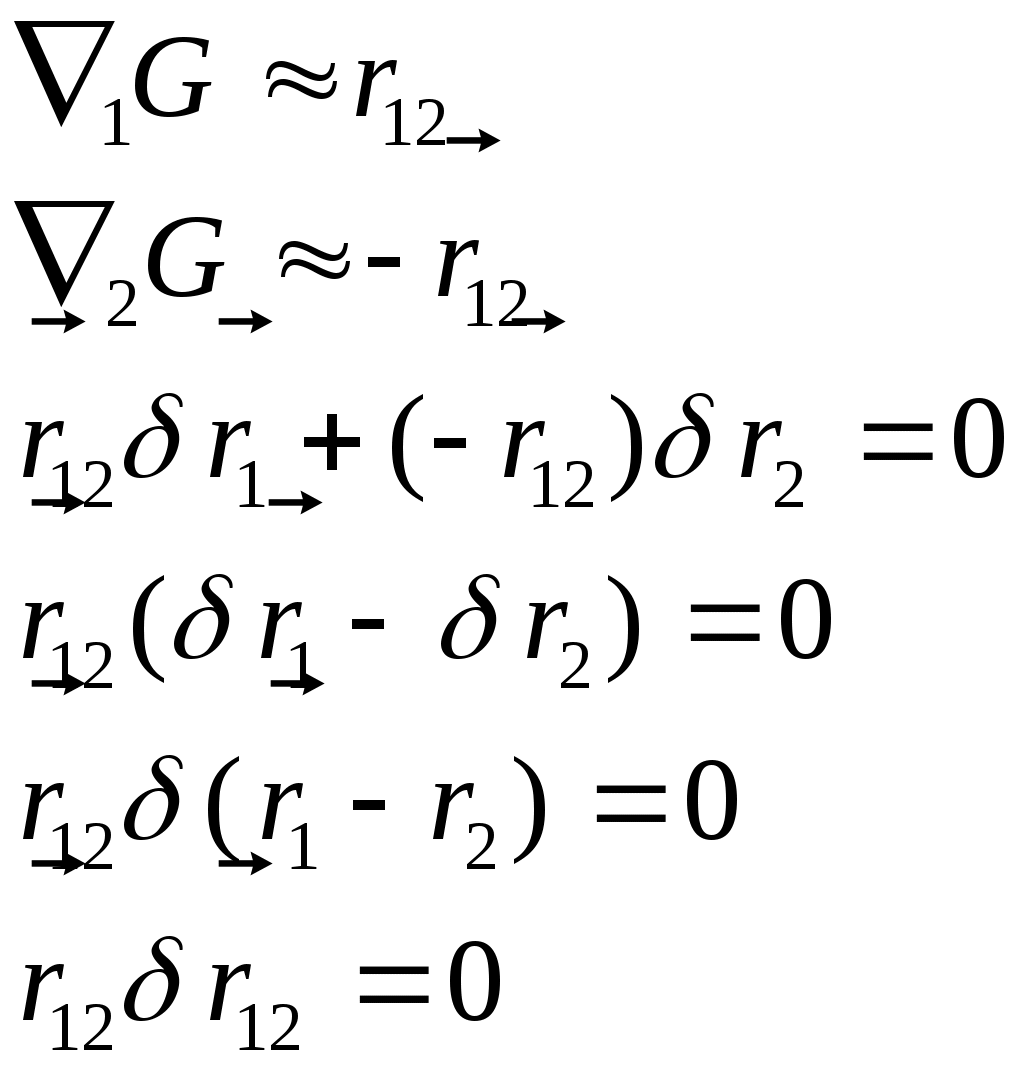
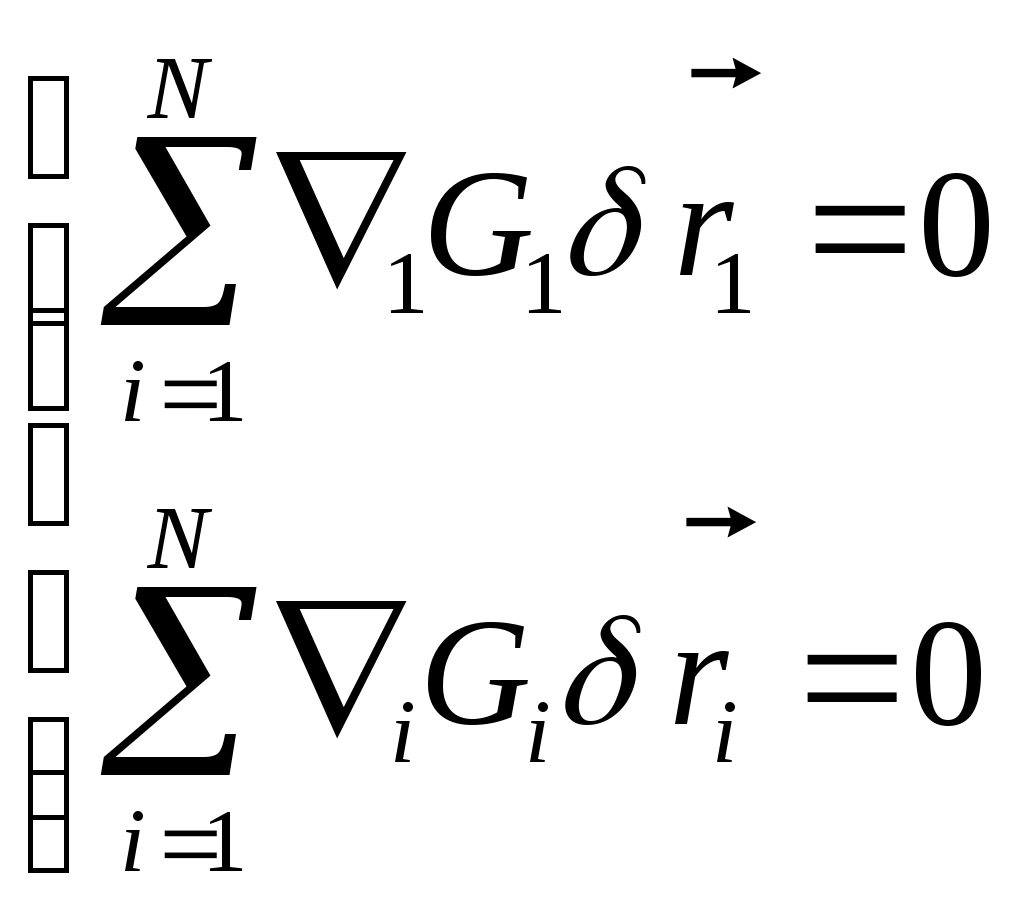 Показ. связь м\д ВП. Перепишем их в скалярной форме.
Показ. связь м\д ВП. Перепишем их в скалярной форме. 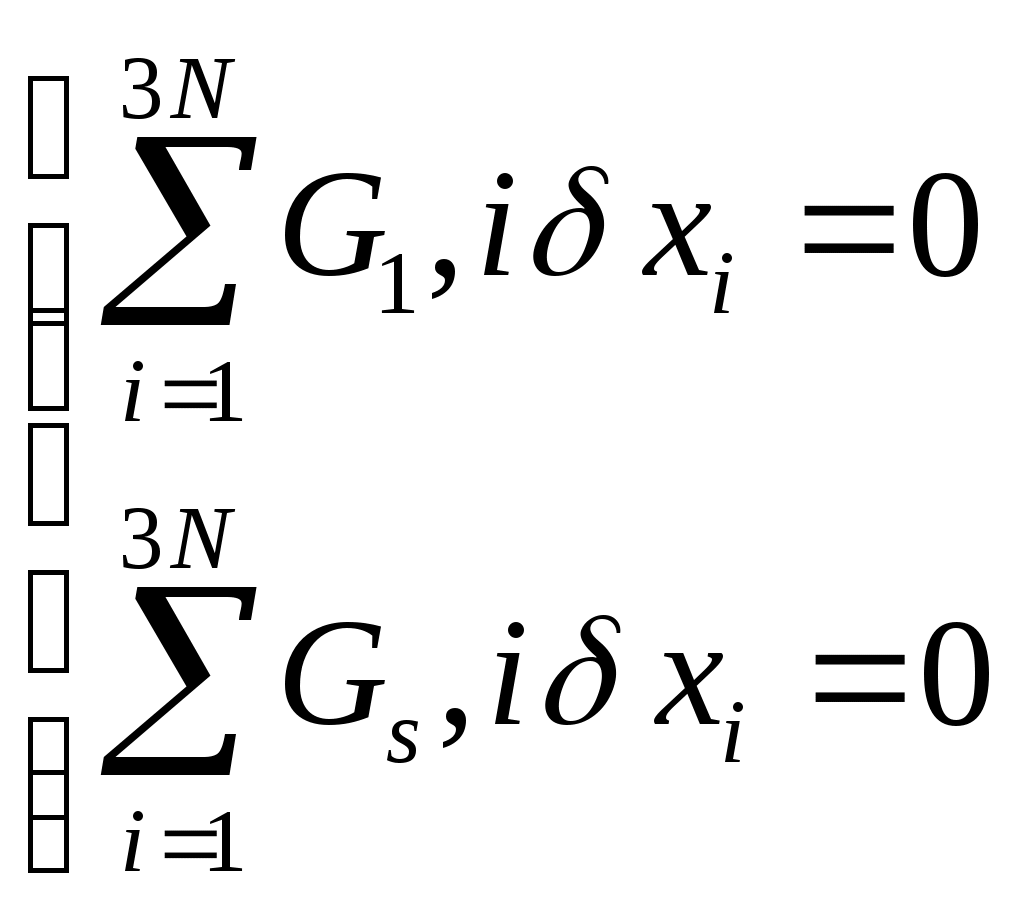 Добавилось еще S ур-ий. Всего 6N неизвестных, 3N+S ур-ий. Чтобы число уравнений совпало с числом неизвестных исп-ем пр-п Даламбера. Вирт. раб. сил реакций:
Добавилось еще S ур-ий. Всего 6N неизвестных, 3N+S ур-ий. Чтобы число уравнений совпало с числом неизвестных исп-ем пр-п Даламбера. Вирт. раб. сил реакций: 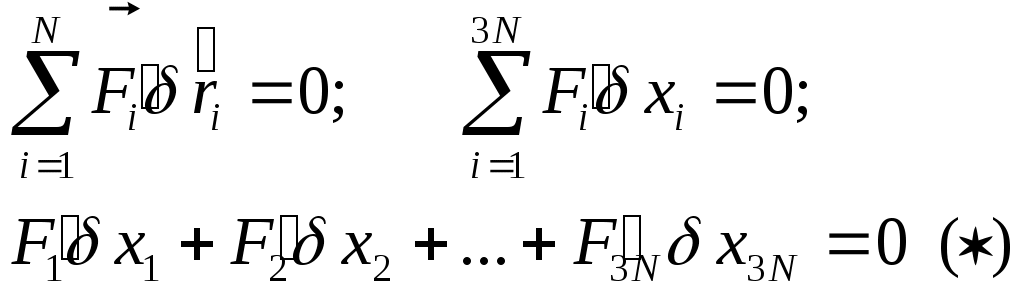 Если бы δxi , были независимы, то (*) было бы 3N ур-ий, но они не все независимы. Из 3N вариаций δxi независимых только 3N-S. 3N+S+3N-S=6N независимых переменных. Т.о. можно решить сист. ур-ий. x1,…,x3N переменных, F’1,…,F3N. Пр-п Даламбера:
Если бы δxi , были независимы, то (*) было бы 3N ур-ий, но они не все независимы. Из 3N вариаций δxi независимых только 3N-S. 3N+S+3N-S=6N независимых переменных. Т.о. можно решить сист. ур-ий. x1,…,x3N переменных, F’1,…,F3N. Пр-п Даламбера: 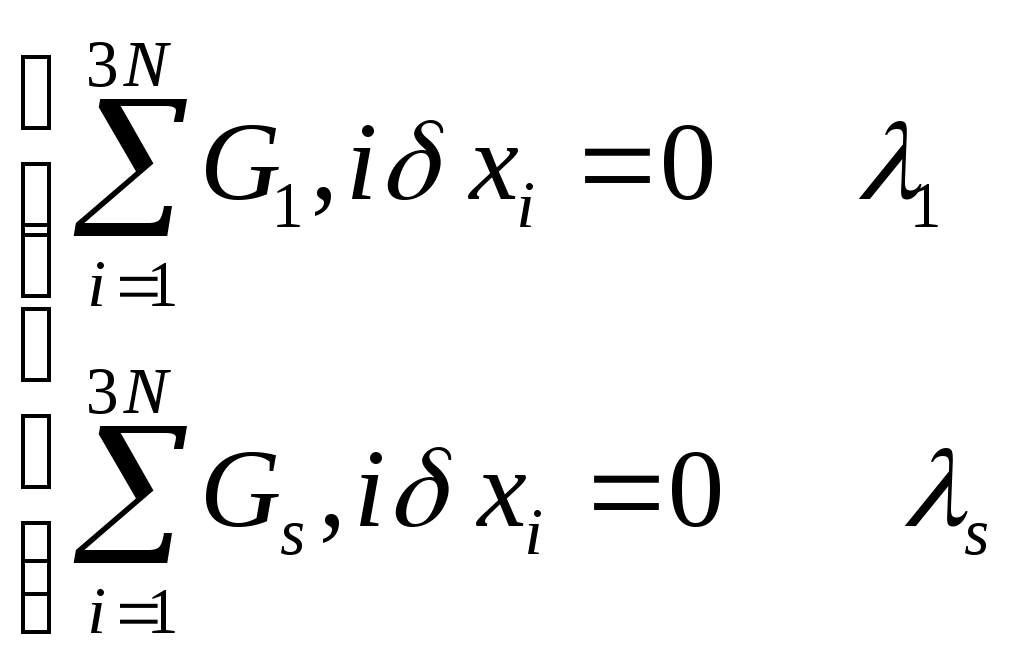
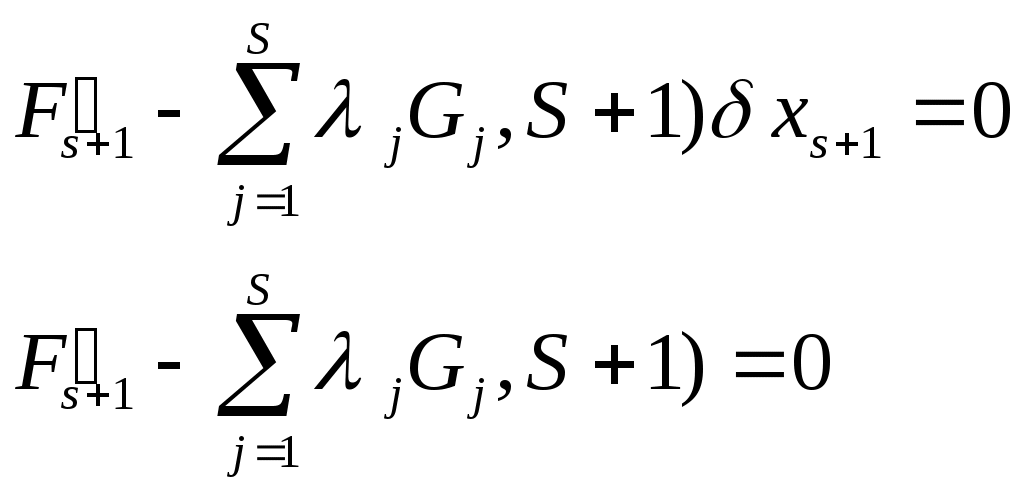 δxS+2 не равным 0 и т.д. Все эти компоненты удовлетворяют одному и тому же ур-ю. Запишем их в общем виде:
δxS+2 не равным 0 и т.д. Все эти компоненты удовлетворяют одному и тому же ур-ю. Запишем их в общем виде: 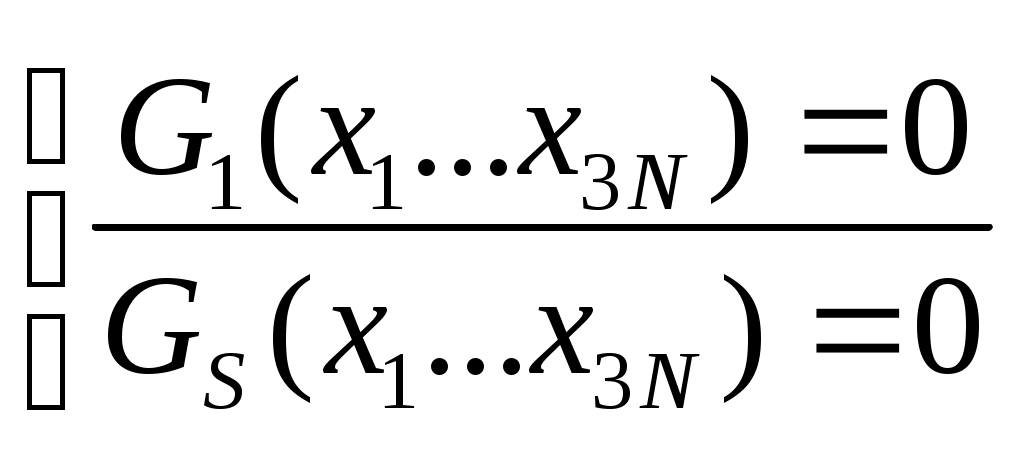 Перепишем.
Перепишем.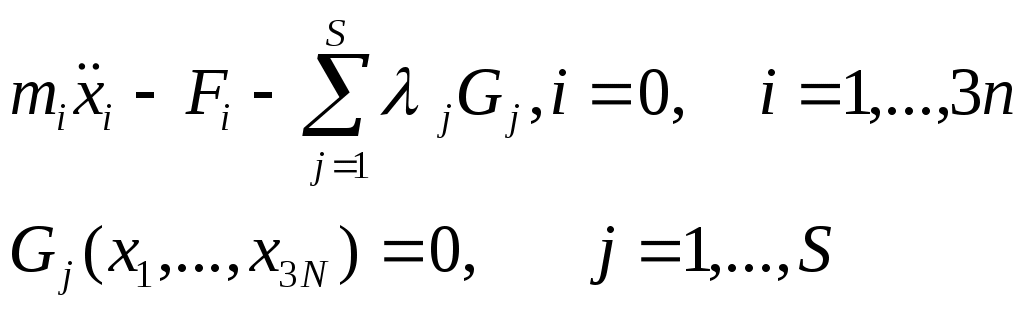 Ур-е Лагранжа I рода.
Ур-е Лагранжа I рода.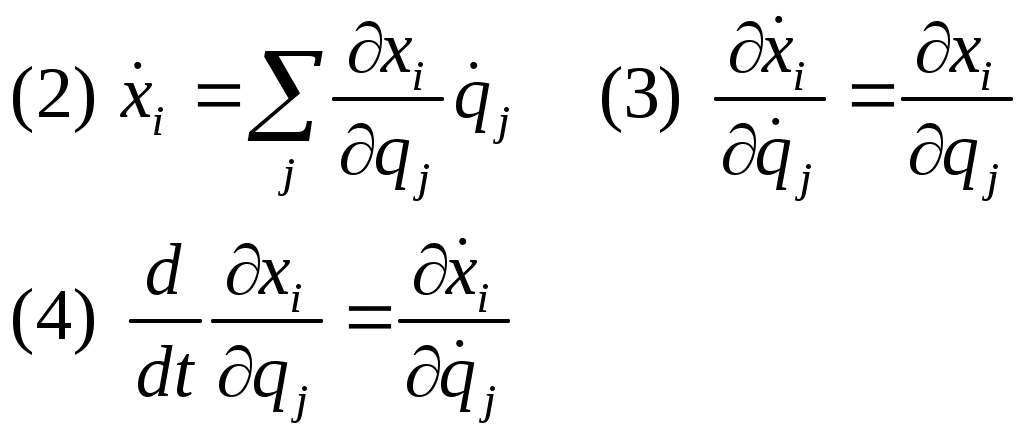 Если система движется, то все qj явл-ся функциями времени, тогда xi, зависящее от qj зависящих от t, то декартовы координаты тоже будут зависеть от t.
Если система движется, то все qj явл-ся функциями времени, тогда xi, зависящее от qj зависящих от t, то декартовы координаты тоже будут зависеть от t. 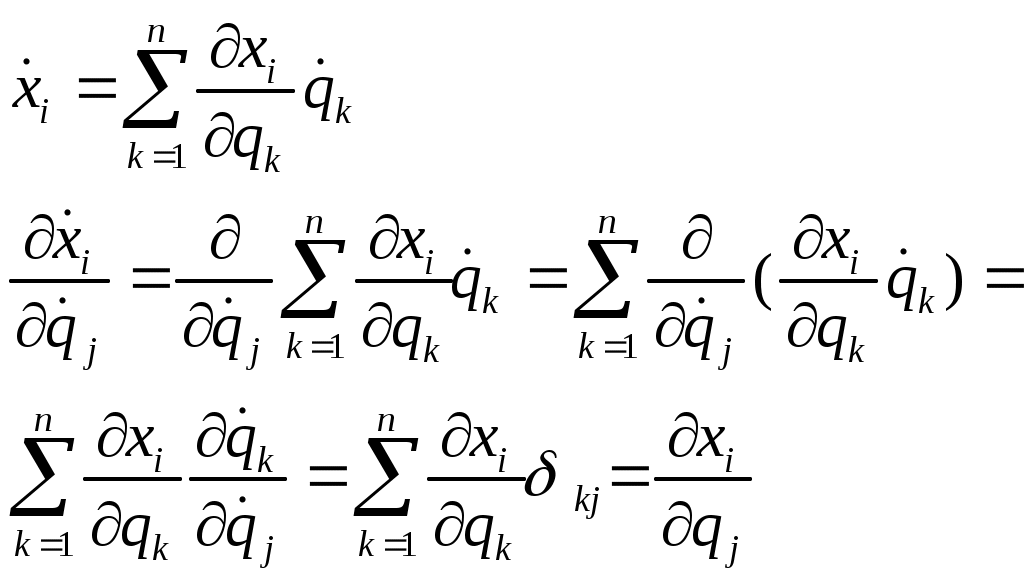 (3 лемма).
(3 лемма).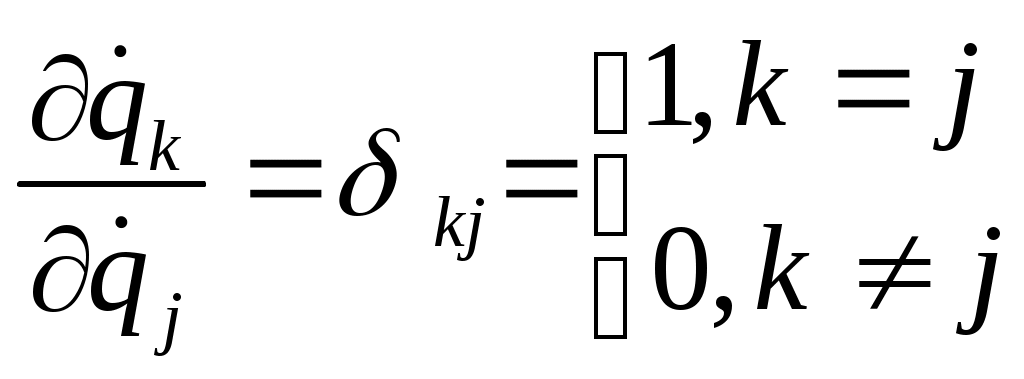 символ Кронекера.
символ Кронекера.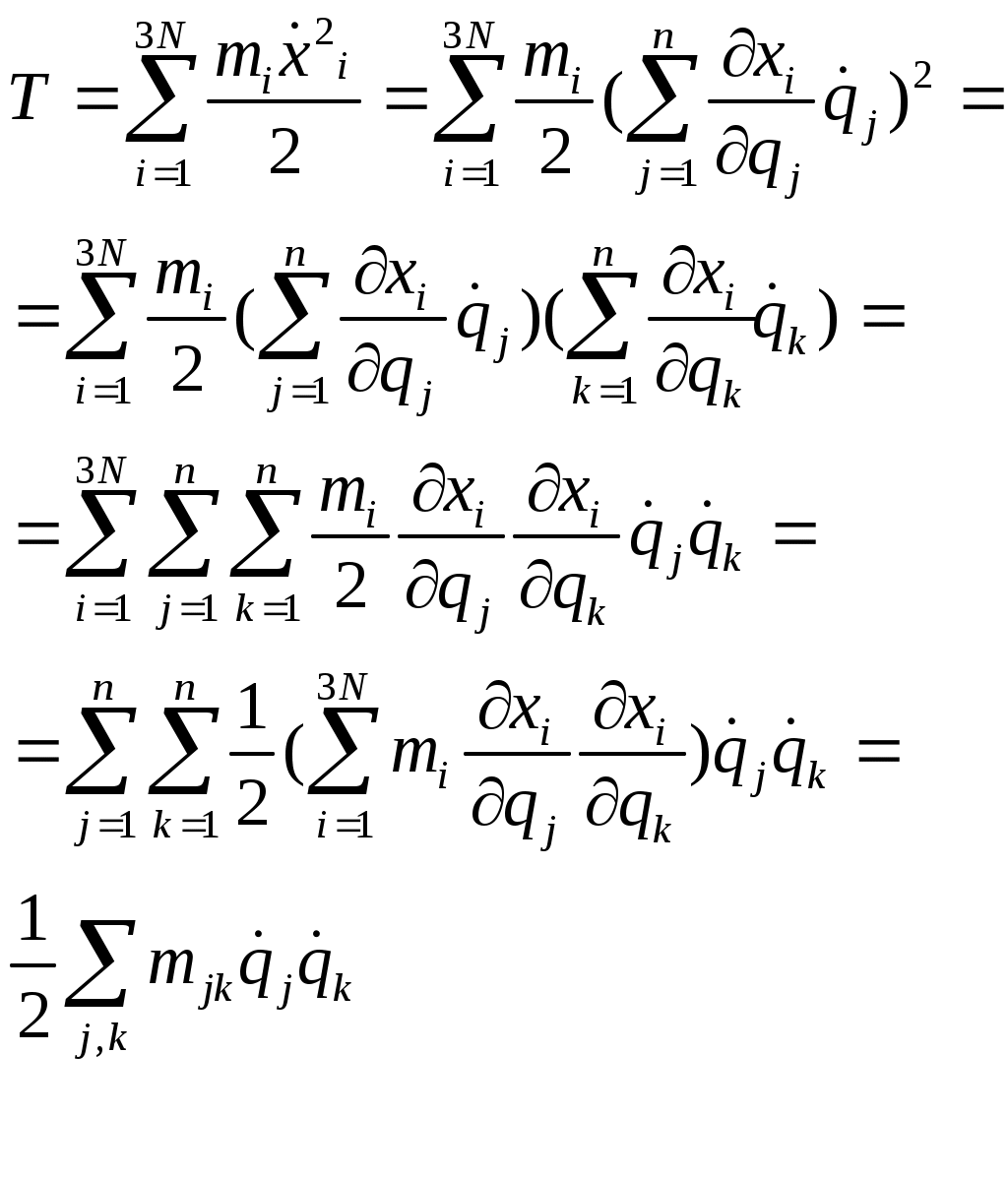
 dN величина «-». Если понимать под dN число частиц dN(θ< θ’< θ+d θ) чтобы она была «+», надо
dN величина «-». Если понимать под dN число частиц dN(θ< θ’< θ+d θ) чтобы она была «+», надо 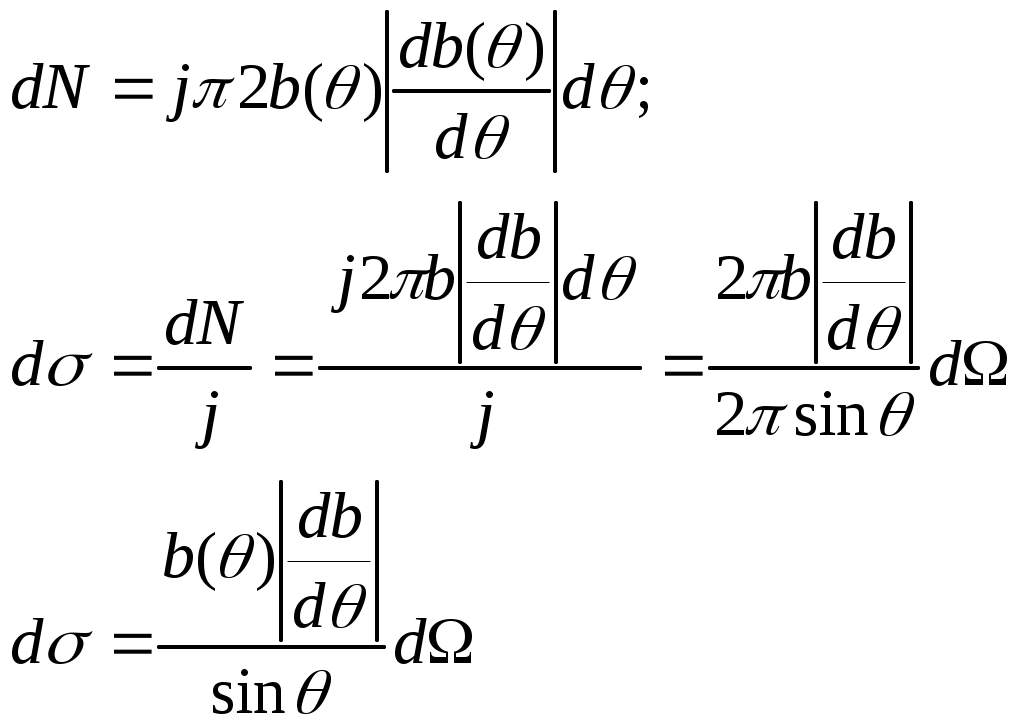
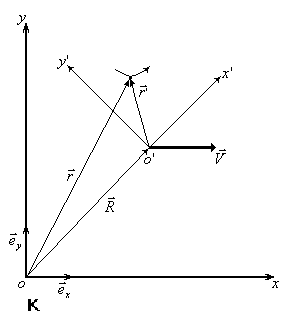 С бескон. мн-во, они движутся поступательно. Неин. сист. — вращающиеся. В ней закон Ньютона несправедлив. Чтобы был справедлив, нужно добавить силу инерции Fин.
С бескон. мн-во, они движутся поступательно. Неин. сист. — вращающиеся. В ней закон Ньютона несправедлив. Чтобы был справедлив, нужно добавить силу инерции Fин. 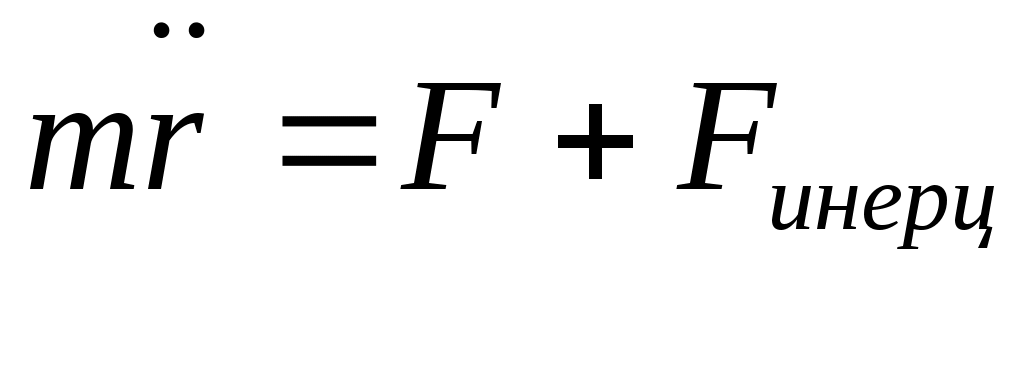
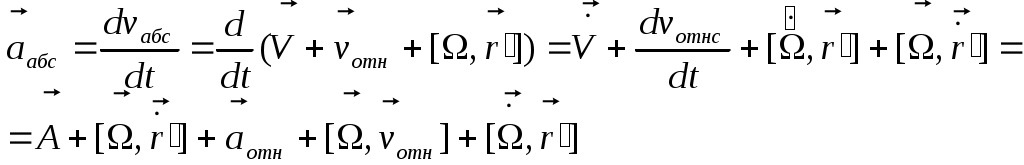
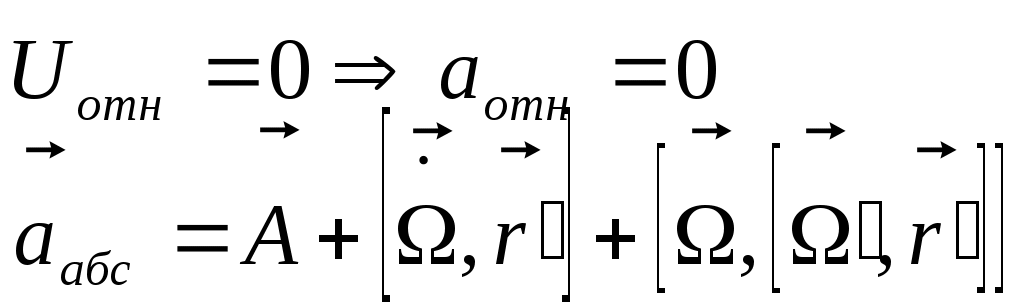
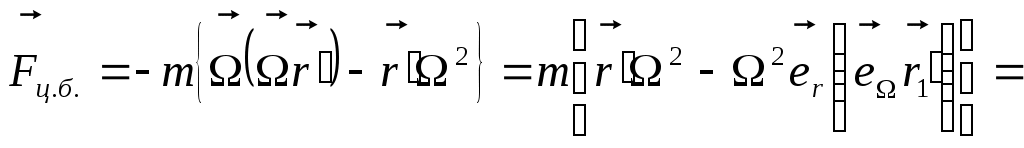
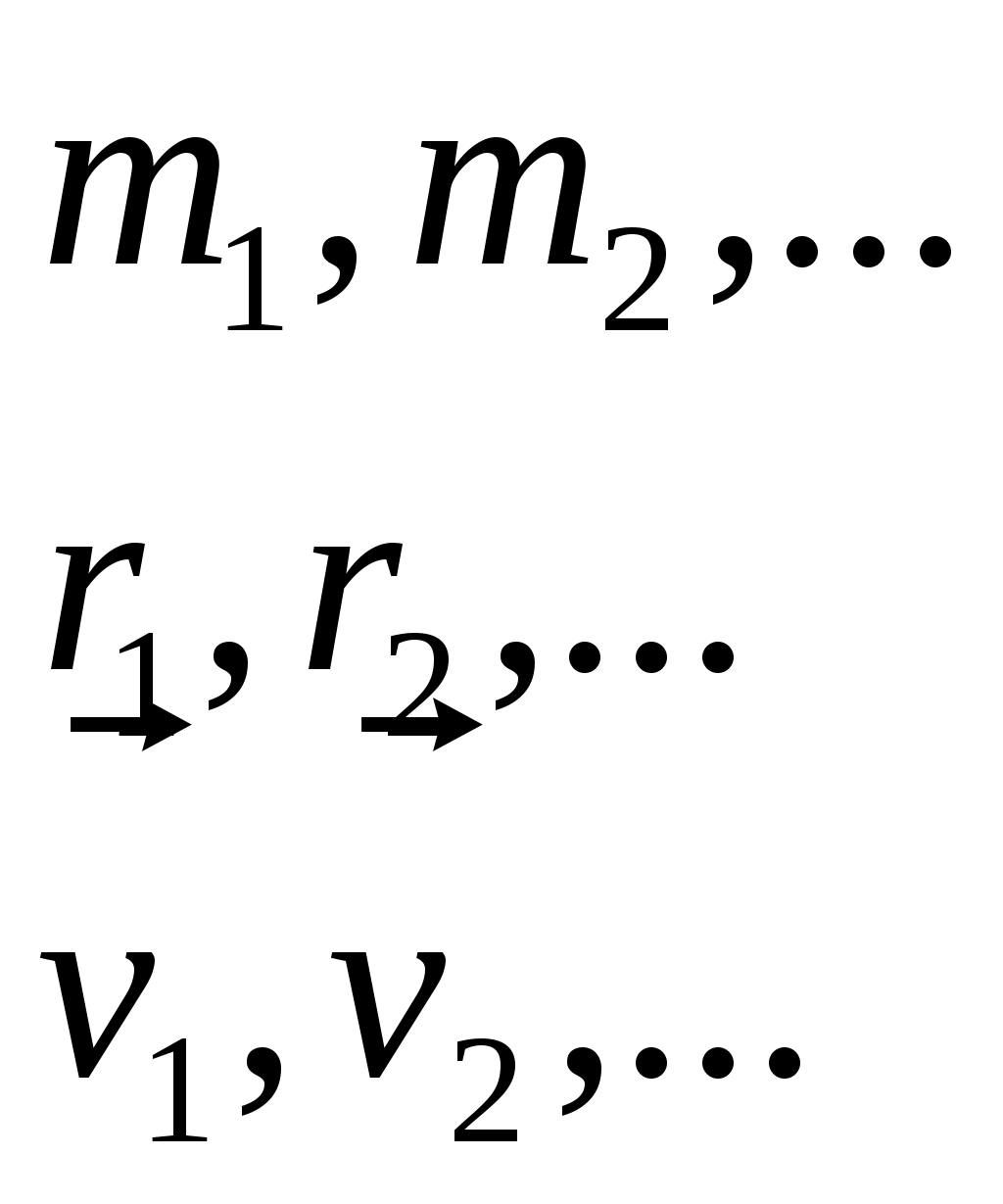
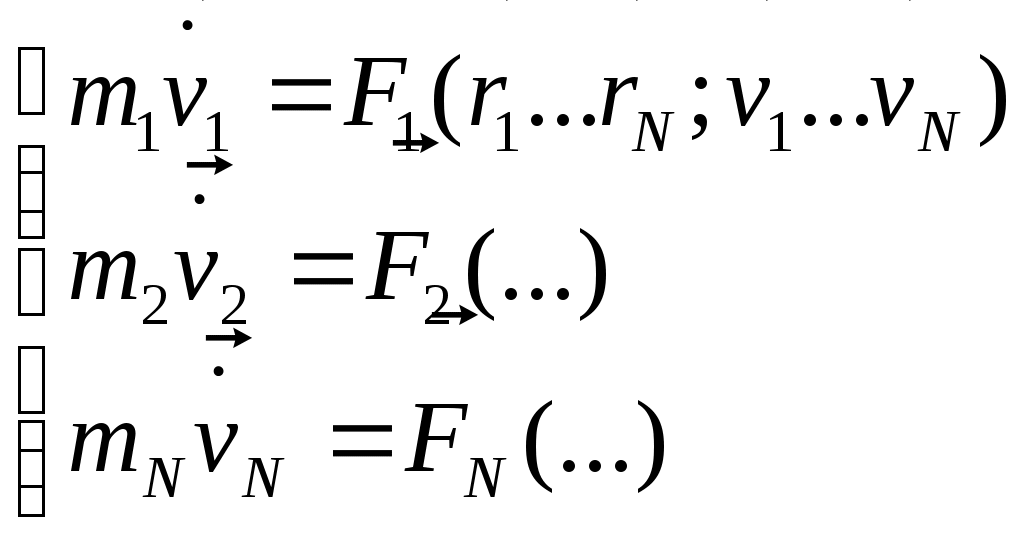 В общем случае. Fi=
В общем случае. Fi=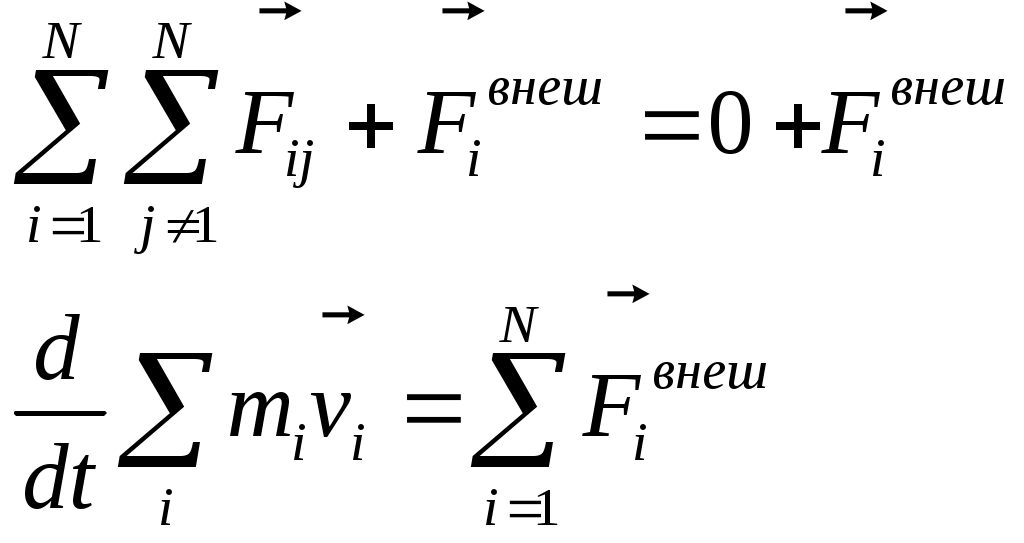
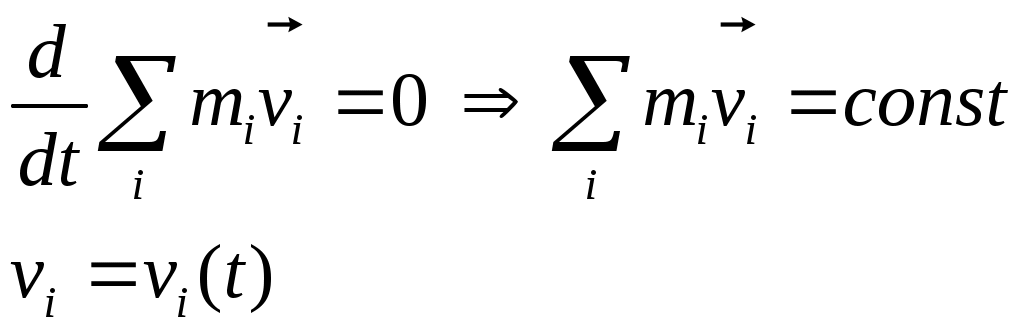 Скорость каждой частицы зависит от времени, но (*), то
Скорость каждой частицы зависит от времени, но (*), то 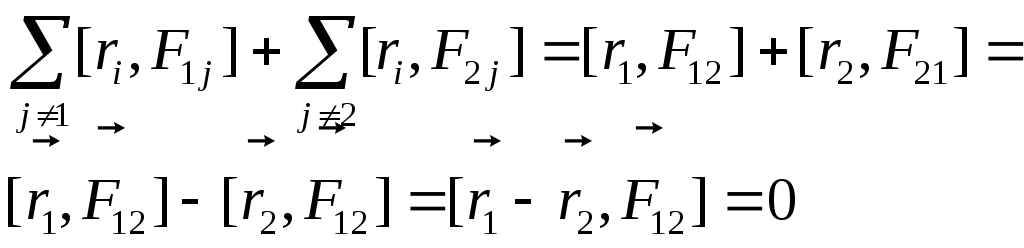 (для центральных сил). Если силы центральные, то сила взаимодействия лежит на одной прямой с вектором
(для центральных сил). Если силы центральные, то сила взаимодействия лежит на одной прямой с вектором 