Задача для движения 1 чцы в заданном внешнем поле. Для решения уря надо знать и
 Скачать 1.66 Mb. Скачать 1.66 Mb.
|
1 2 L — мом. имп. М — гл. мом. системы внеш. сил сист. 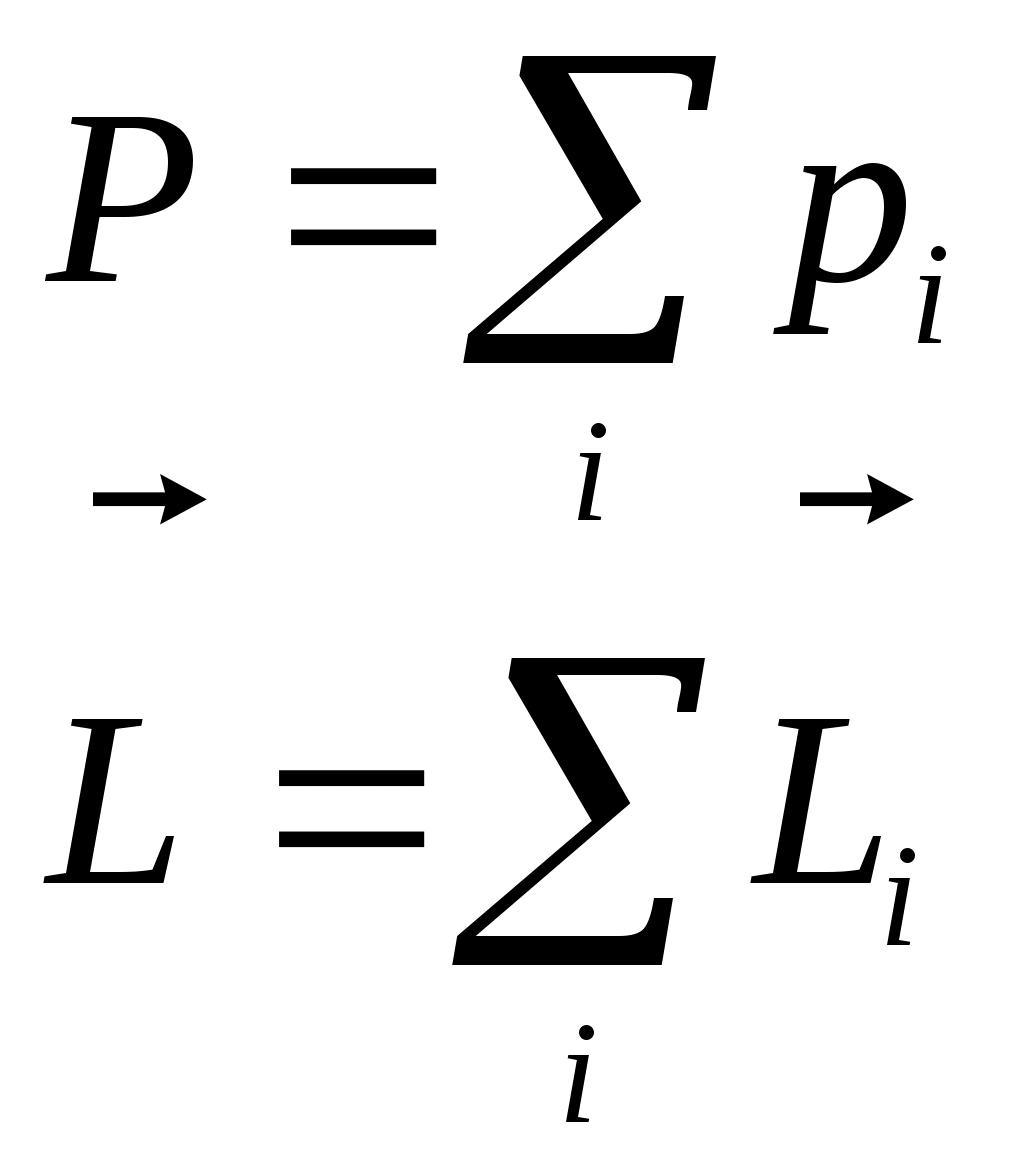 5 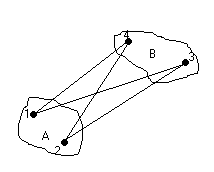 .3. Энергия системы. .3. Энергия системы.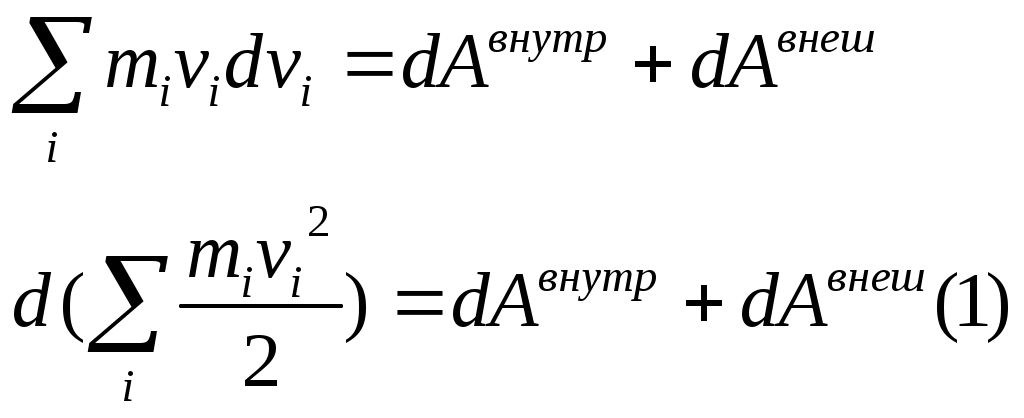 Изменение некоторой величины Изменение некоторой величины 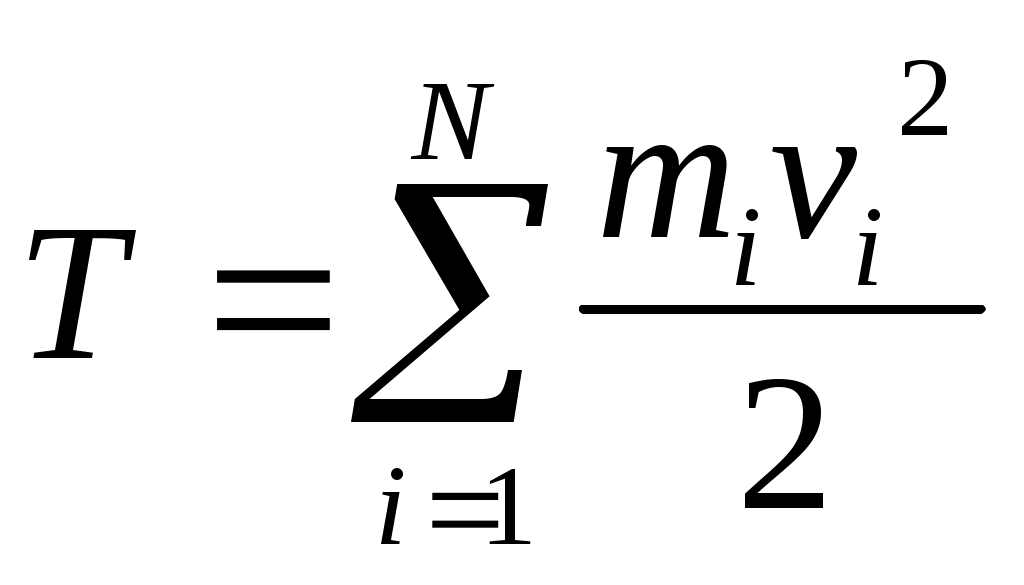 (кин. эн. сист.) Кин. эн-я сохр-ся, если работа внешних сил = 0. Предположим, что внутр. сиды явл-ся силами потенциальными, напр. они центрально-симметричны (кин. эн. сист.) Кин. эн-я сохр-ся, если работа внешних сил = 0. Предположим, что внутр. сиды явл-ся силами потенциальными, напр. они центрально-симметричны (Зависит от координаты и имеет определенную структуру). — несимметричная запись внутр. энергии. Но для удобства перепишем: (завышение потенциальной энергии) (U12+U21+ +U23+U31+ +U23+U32+…+ +UN-1,N,UN,N-1)1/2= (1): 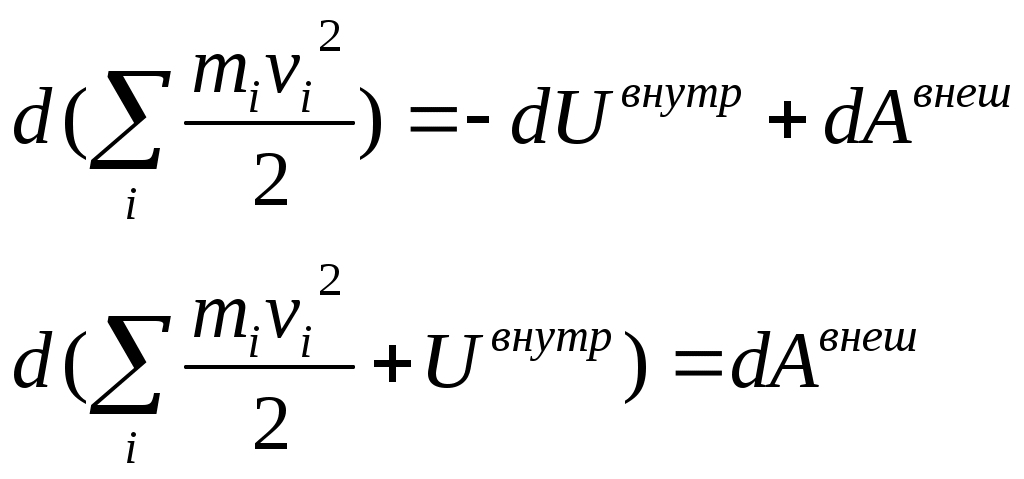 dE=dA — закон сохранения энергии. Полная мех. энергия не обладает св-ми аддитивности, а кин. обладает. Рассмотрим сист., состоящую из 4-х ч-ц. N=4. dE=dA — закон сохранения энергии. Полная мех. энергия не обладает св-ми аддитивности, а кин. обладает. Рассмотрим сист., состоящую из 4-х ч-ц. N=4. 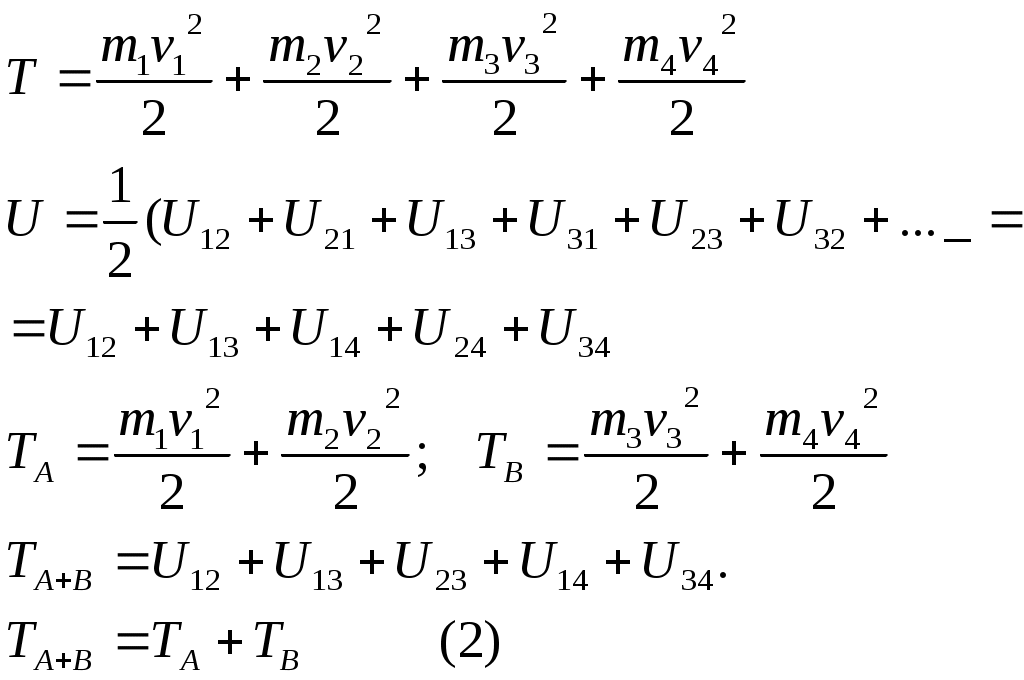 Раздвинем подсистемы далеко друг от друга. Раздвинем подсистемы далеко друг от друга.UAB=UA+UB+UAB (3) Энергия не аддитивна. Сложим (2) и (3). Получим: ЕА+В=ЕА+ЕВ+UАВ. 5.4. Теорема о вариале сил. Р Th о вариале сил: если движение системы происходит в ограниченной области пр-ва и с ограниченными по модулю скоростями, то средняя по времени кин. энергия системы равна среднему по времени вариалу сил. 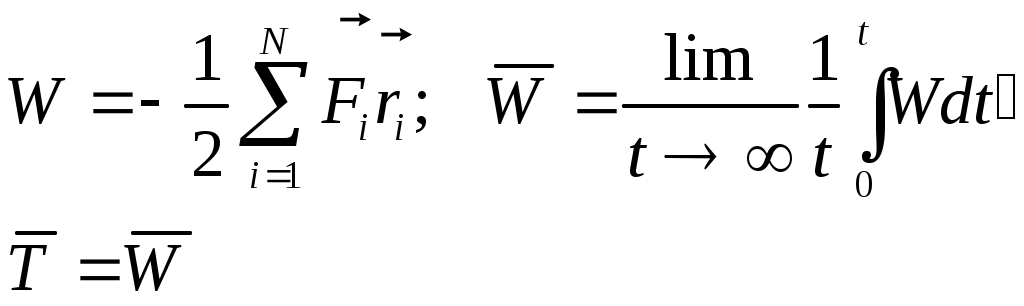 Док-во: Возьмем ур-е Ньютона и просумир-ем: 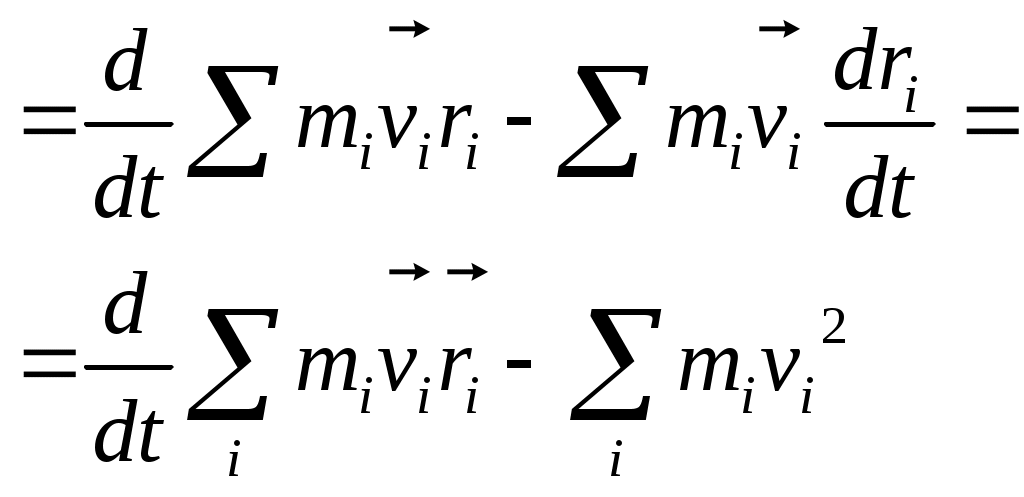 Левая часть. Приравниваем к правой: Левая часть. Приравниваем к правой: 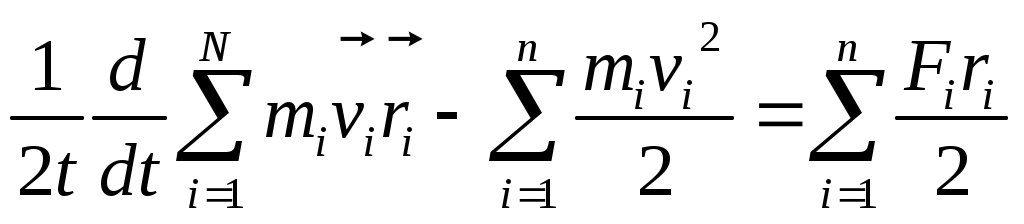 Интегрируем: 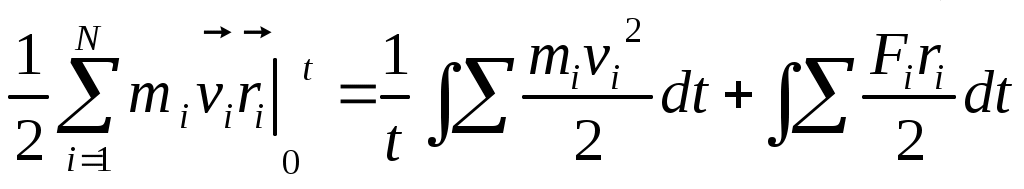 Разделим на dt: если движение происходит с ограниченными по величине скоростями, то |vi| 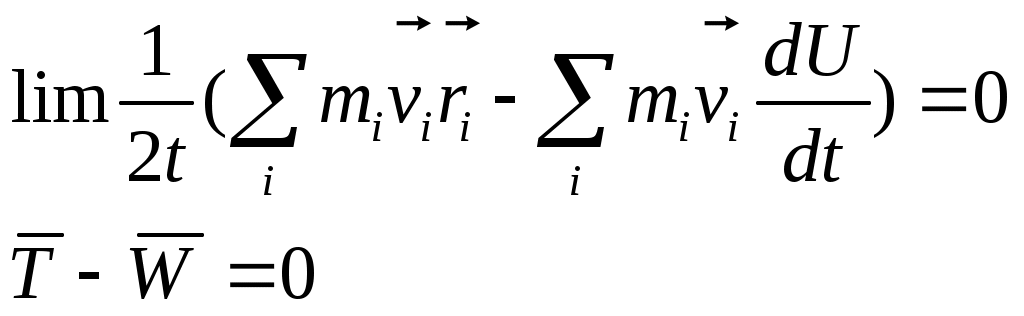 5.5. Система центра масс (СЦМ). 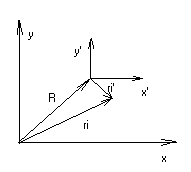 центр масс центр масс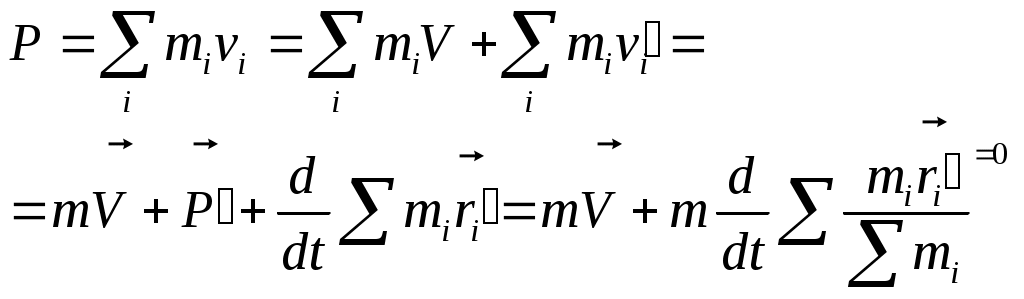 Последнее слагаемое — вектор, проведенный из начала штрихованной СК в центр масс, но нач. штрих. сист. нах-ся в центре масс, то он = 0. То импульс сист. P=mV , V — ск-ть, воображаемой точки из центра масс. Момент импульса в ЛСК: Последнее слагаемое — вектор, проведенный из начала штрихованной СК в центр масс, но нач. штрих. сист. нах-ся в центре масс, то он = 0. То импульс сист. P=mV , V — ск-ть, воображаемой точки из центра масс. Момент импульса в ЛСК: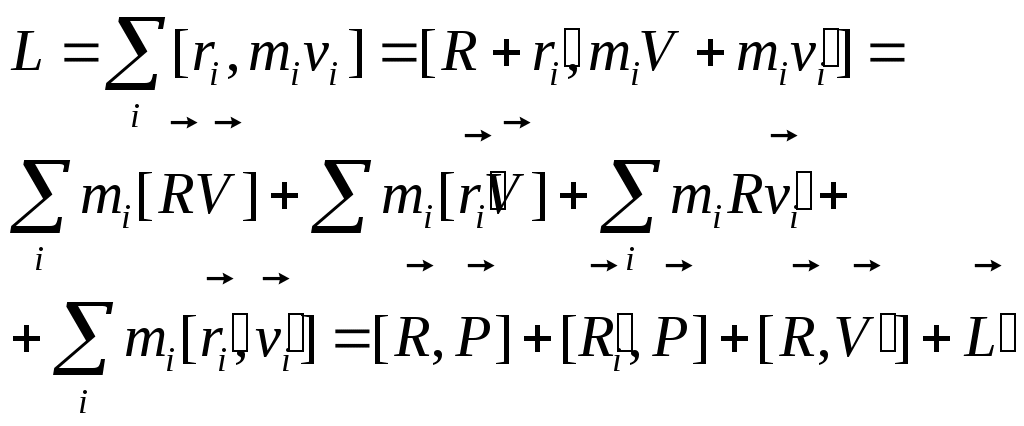 Тогда Тогда 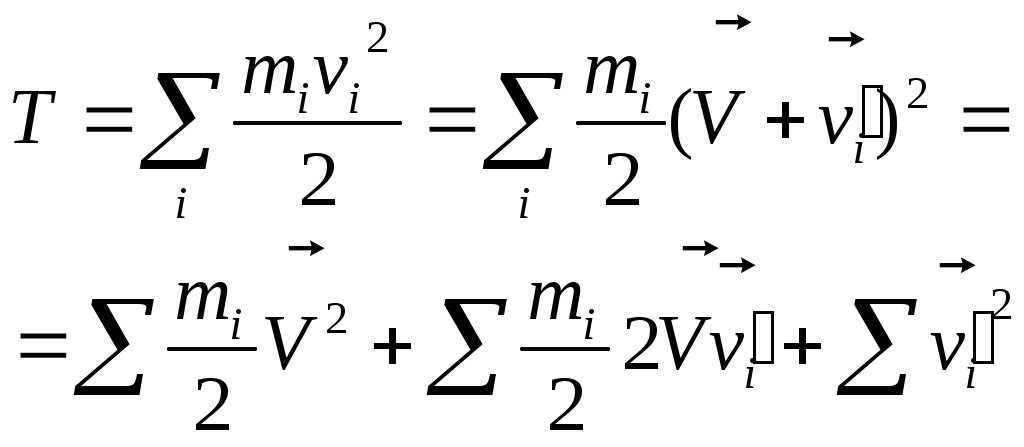 От i зависит только m, то От i зависит только m, то 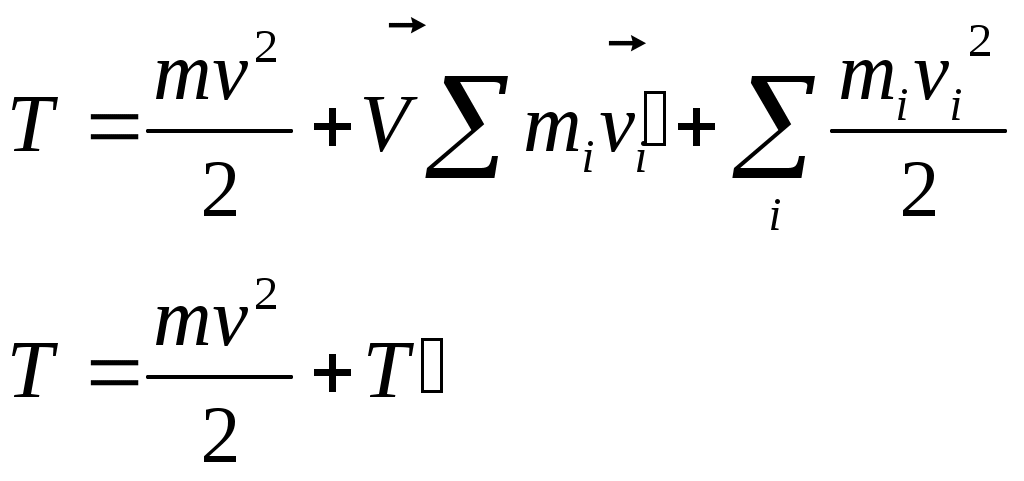 Кин. энергия ЛСК = кин. эн. ЦМ имеющего суммарную массу. T’ — внутр. кин. эн. сист. отн-но ее ЦМ. Т.к. сист. замкнута, то Кин. энергия ЛСК = кин. эн. ЦМ имеющего суммарную массу. T’ — внутр. кин. эн. сист. отн-но ее ЦМ. Т.к. сист. замкнута, то 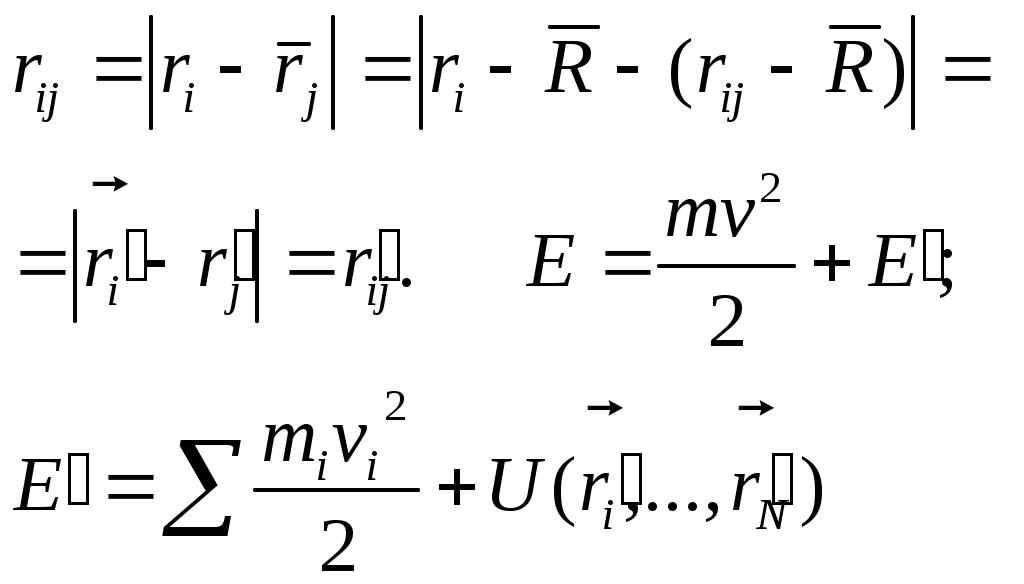 — внутр. энергия. — внутр. энергия.3.1. Соотношение м\д углом рассеяния и эксцентриситетом. И 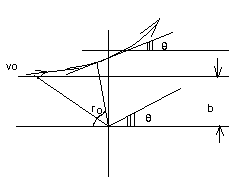 нфинитное движение – точка приходит из бесконечности и уходит в бесконечность. нфинитное движение – точка приходит из бесконечности и уходит в бесконечность.ro-минимальное расстояние между частицой и силовым центром Из рисунка видно что Из (1) 3.2 Прицельный параметр и угол рассеяния b  (прицельный параметр)- расстояния на котором прошла бы частица от силового центра, если частица двигалась по прямой , т.е. не было взаимодействий.С пом. b можно определить момент импульса L=mvb Полная энергия: (прицельный параметр)- расстояния на котором прошла бы частица от силового центра, если частица двигалась по прямой , т.е. не было взаимодействий.С пом. b можно определить момент импульса L=mvb Полная энергия: 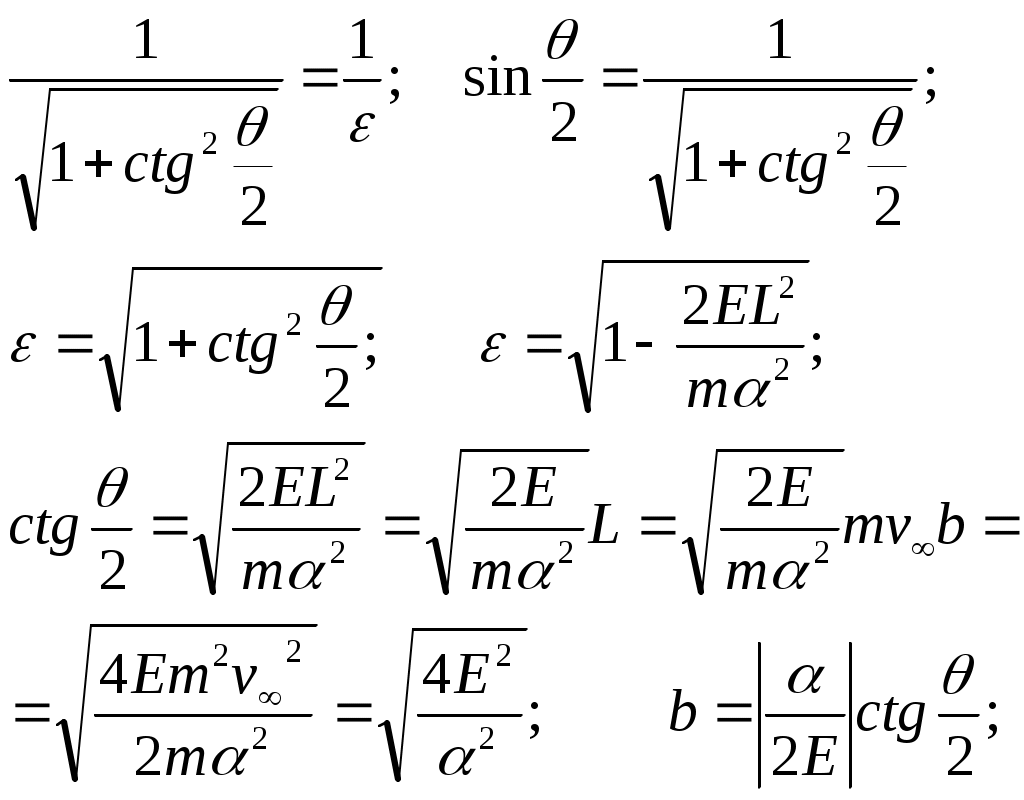 3.4. Сечение рассеивания Резерфорда. Ч 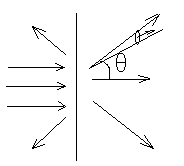 астицы отталкиваются от пластинки и проходят сквозь нее. Телесный угол dΩ на угол θ, j — число частиц, падающих на площадку. N(dΩ) — число рассеянных частиц в тел. угле dΩ за то же время. Отношение этого числа к плотности потока падающих частиц j и является то, тчо мы называем диф-ым сечением рассеивания ч-ц в телесный угол dΩ. астицы отталкиваются от пластинки и проходят сквозь нее. Телесный угол dΩ на угол θ, j — число частиц, падающих на площадку. N(dΩ) — число рассеянных частиц в тел. угле dΩ за то же время. Отношение этого числа к плотности потока падающих частиц j и является то, тчо мы называем диф-ым сечением рассеивания ч-ц в телесный угол dΩ. 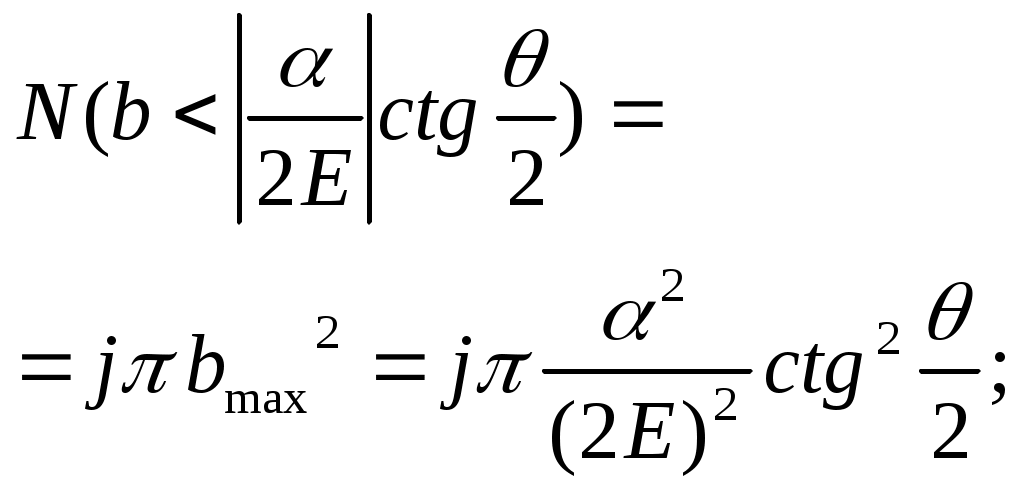 . Найдем число этих частиц. Возьмем плотность потока, умножим на величину площади круга, подсчитаем телесный угол, соответствующий . Найдем число этих частиц. Возьмем плотность потока, умножим на величину площади круга, подсчитаем телесный угол, соответствующий 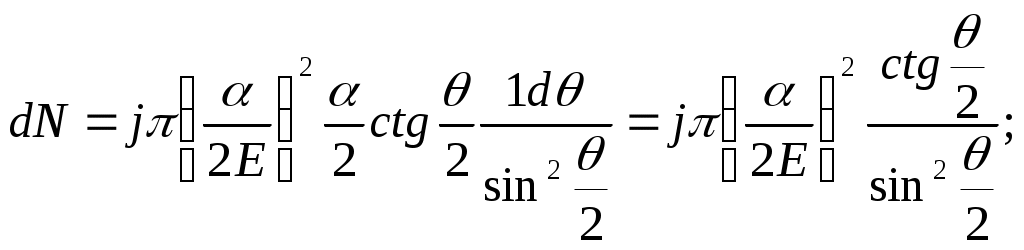 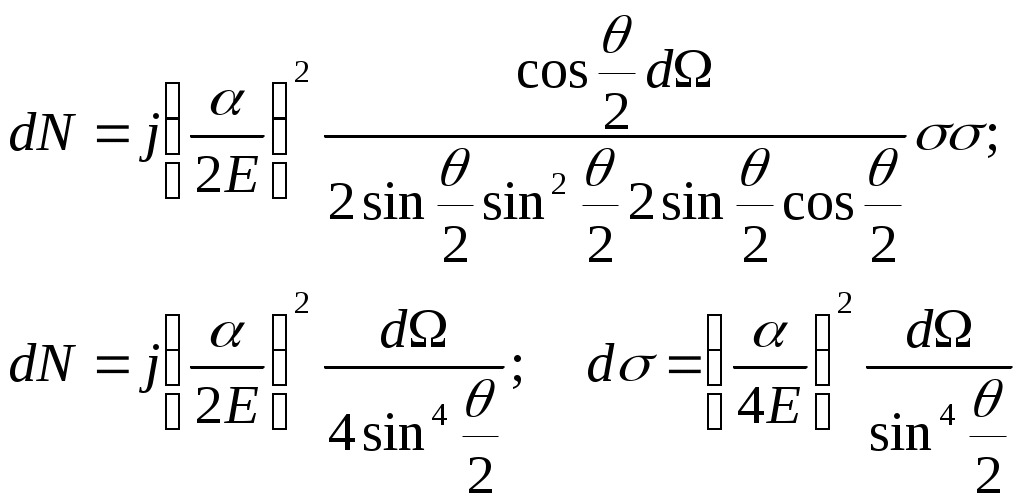 — формула Резерфорда. — формула Резерфорда.2.1.Сохранение энергии и момента импульса в центральном симметричном поле (ЦСП). Рассм. матер. точку — физ. Тело разм. к-ого можно принебр. В усл. данн. задачи (но! излуч., вращ.). мат. точка – физ. тело для к-ого существ (характерна) только масса и дв-е его под дейсв физ силы. Матер точка (наз её «точка») – это не геом точка. Дв-е мат точки – дв-е от одной к др геом точке и 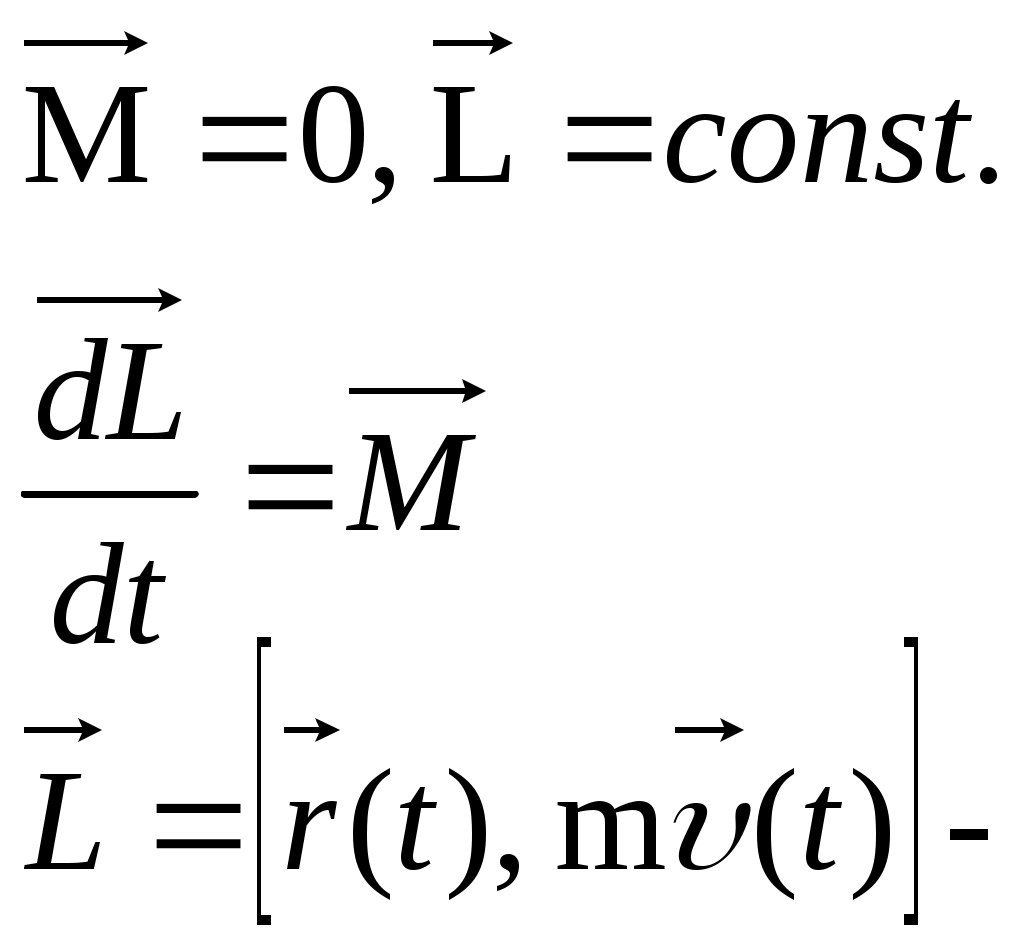 з (1) и (2) видно, что з (1) и (2) видно, что 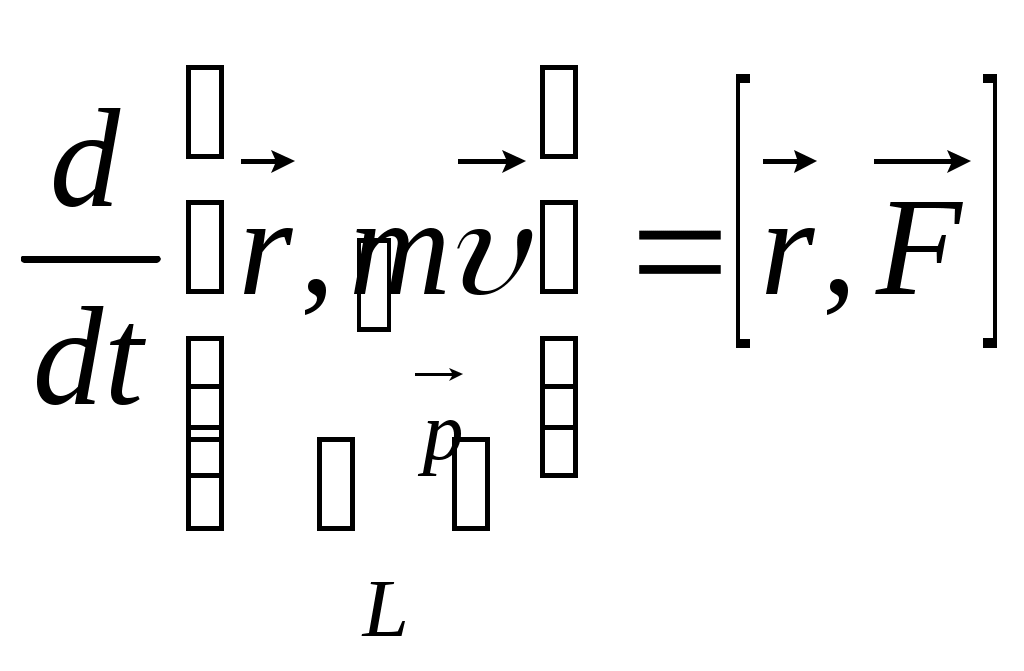 -опр-е мом-а имп-а НО! нов точка треуг, плоск к-ого перп L, след частица двиг в плоск перп L след рассм двумерн дв-е в ОХУ О В 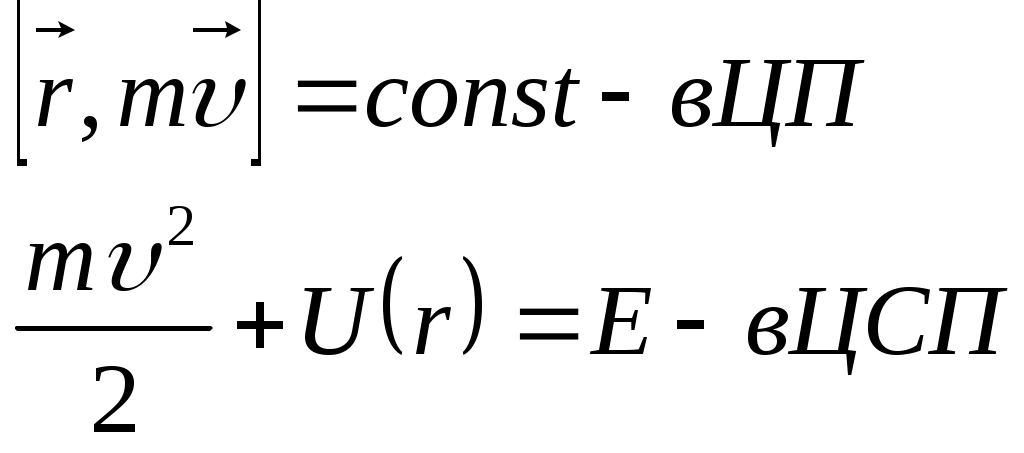 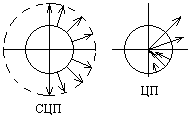 центр поле закон сохр мом импульса: центр поле закон сохр мом импульса: 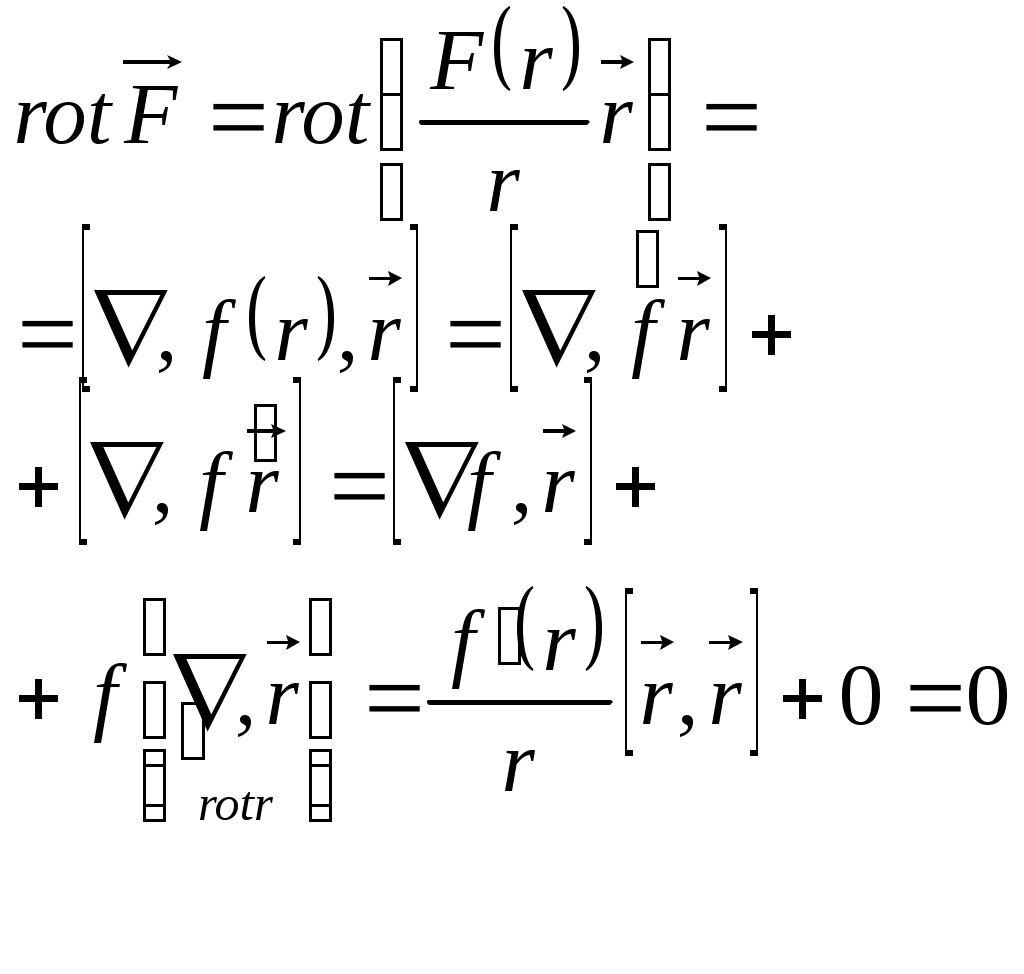 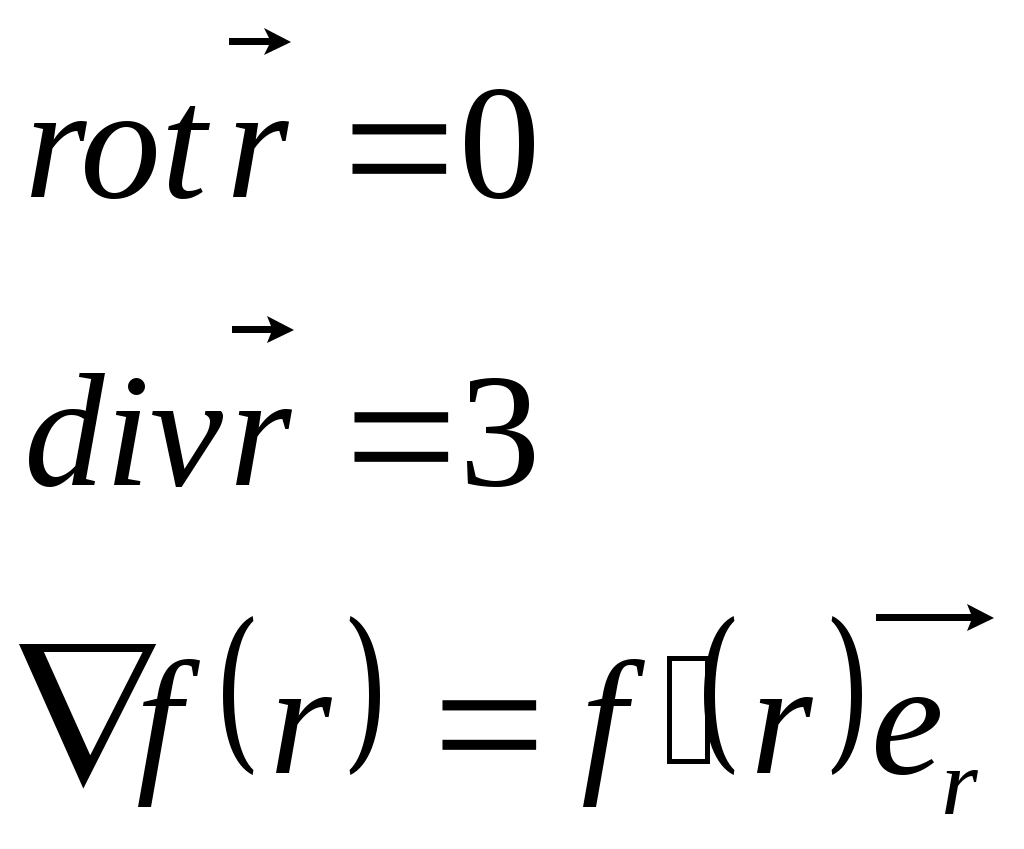 rot ЦСС=0 , след она потенц., след rot ЦСС=0 , след она потенц., след 2.2 Эффективная потенциальная энергия. В x = rcosφ y = rsinφ дифференцируя эти выражения возведём с квадрат и сложим: получим полярные координаты 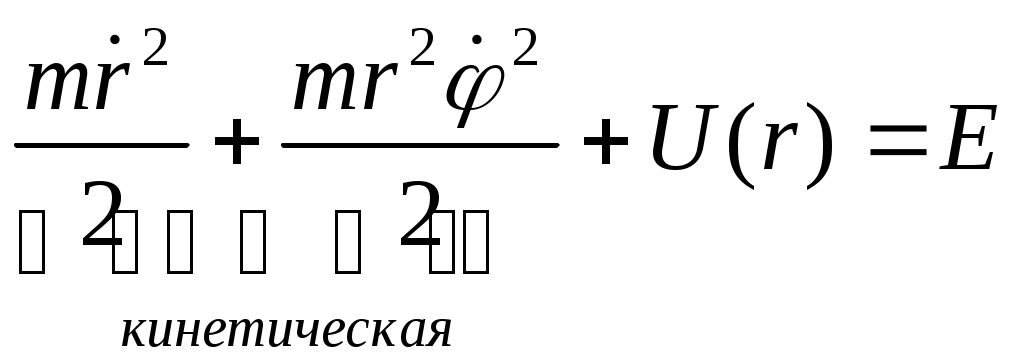 найдём из 2-го 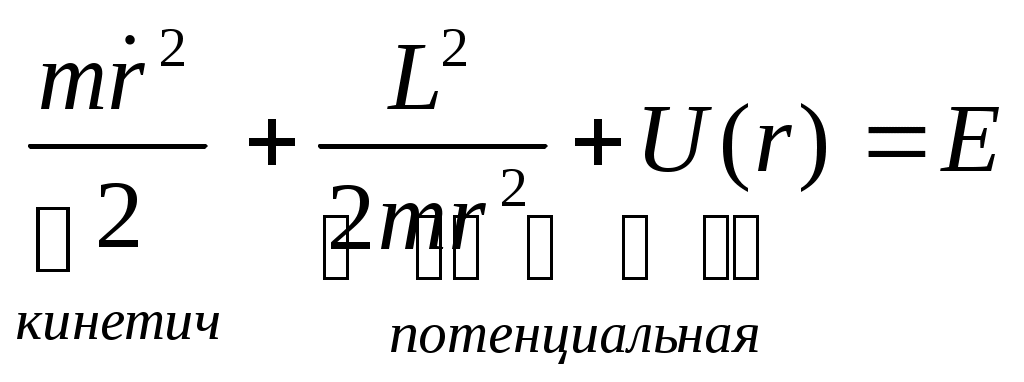 о Но! Только при Э 2.3 Траектория в ЦСП 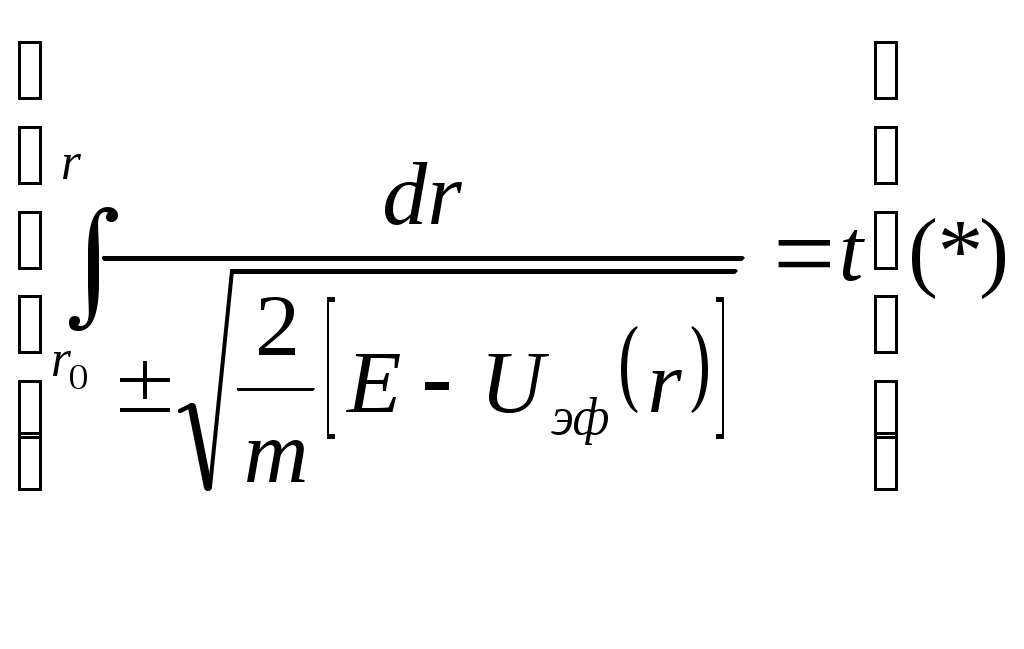 опр. из п.1.4 из закона сохранения импульса 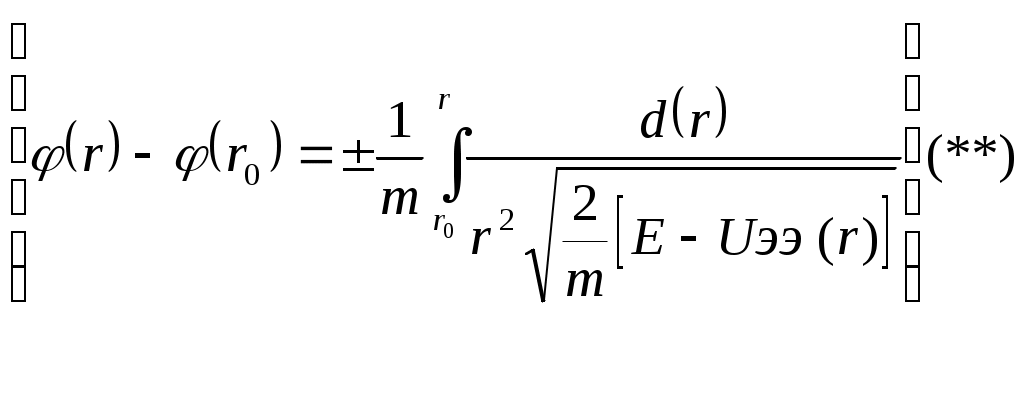 (*) – обр. к иск. ф-ии , найдя r(t) подст. в (**) и тогда задача будет решена. 2.4. Эффективный потенциал Кулоновского поля. Кул поле 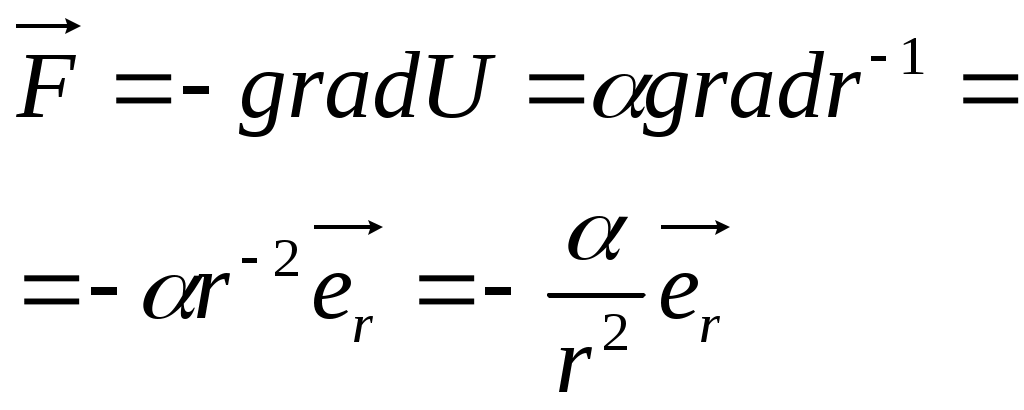 Ф-я от расст-я f=f(r) Ф-я от расст-я f=f(r) Т 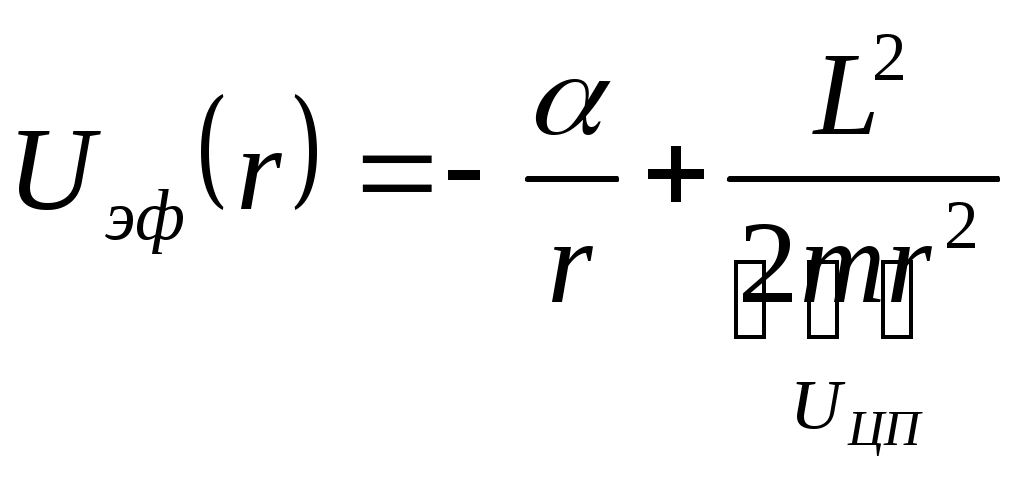 Рассм частн случ: притяж-е R-раст до мин зн-я эф энерг Найти полож-е R В случае когда 2)отталкивание (α<0) только инфинитное дв-е Разделение переменных в уравнении Ньютона. Одномерное движение под действием силы F(t). Одномерное движение под действием силы F(v). Движение частицы в поле силы, зависящей от координаты F(x)/ К 2.1. Сохранение энергии и момента импульса в центральном симметричном поле.(ЦСП) 2 2.3. Траектория в ЦСП. 2.4. Эффективный потенциал Кулоновского поля. Р Траектория в кулоновском поле. Классификация траекторий в кулоновском поле Соотношение «угол рассеяния — Эксцентриситет» Прицельный параметр и угол рассеяния Сечение рассеяния Резерфорда. Общая формула теории рассеяния. 4.1. Угловая скорость. Абсолютная и относительная скорости. Абсолютное и относительное ускорение. Силы инерции. Импульс системы. Момент импульса системы Энергия системы. Теорема о вириале сил. Система центра масс (СЦМ) 6.1. Движение замкнутой системы двух тел. 6.2. Момент импульса и энергия системы 2-х тел. 6.3. Законы Кеплера. 6.4. Упругое столкновение — диаграмма импульса. 6.5. Упругое столкновение — диаграмма скоростей. 7.1. Понятие связи. 7.2. Принцип Даламбера. 7.3. Уравнение Лагранжа I рода. 8.1. Обобщенные координаты и скорость. 8.2. Работа и энергия в обобщенных координатах. 6.4. Упругое столкновение-диаграмма импульсов. у 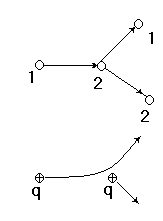 пруг. столк. – где нал. эн. част. и конечн. энерг. част. остаётся неизменным. пруг. столк. – где нал. эн. част. и конечн. энерг. част. остаётся неизменным.До: После Задолго→ д 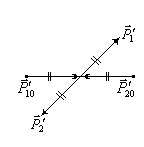 о: о: закон сохр. энерг.: 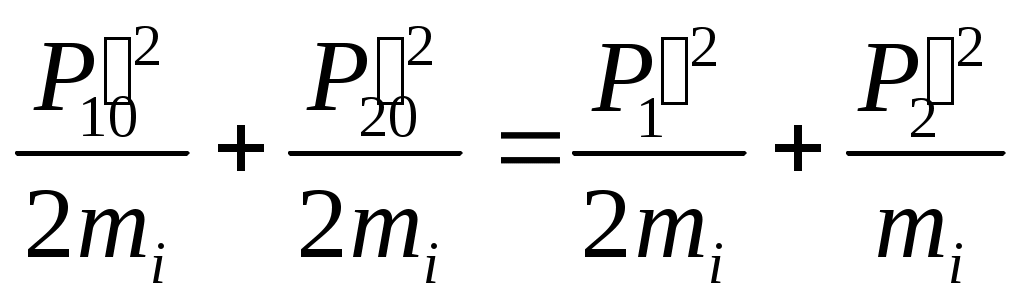 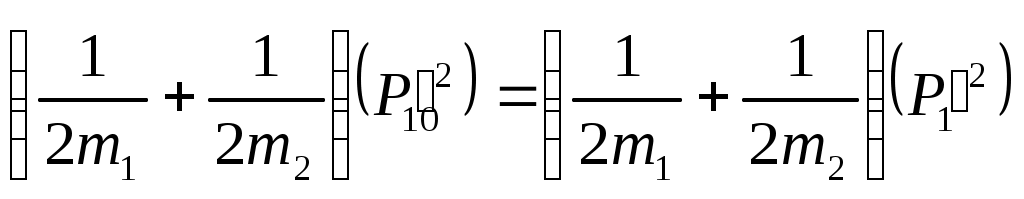 2.5.Радиальная скорость в Кулоновском поле. Е-Uэф=Тr Эф потенц энерг=потенц энерг+азимутальная часть кинетическаой энергии (α-азимут) Тr-кинетич энергия радиальн дв-я 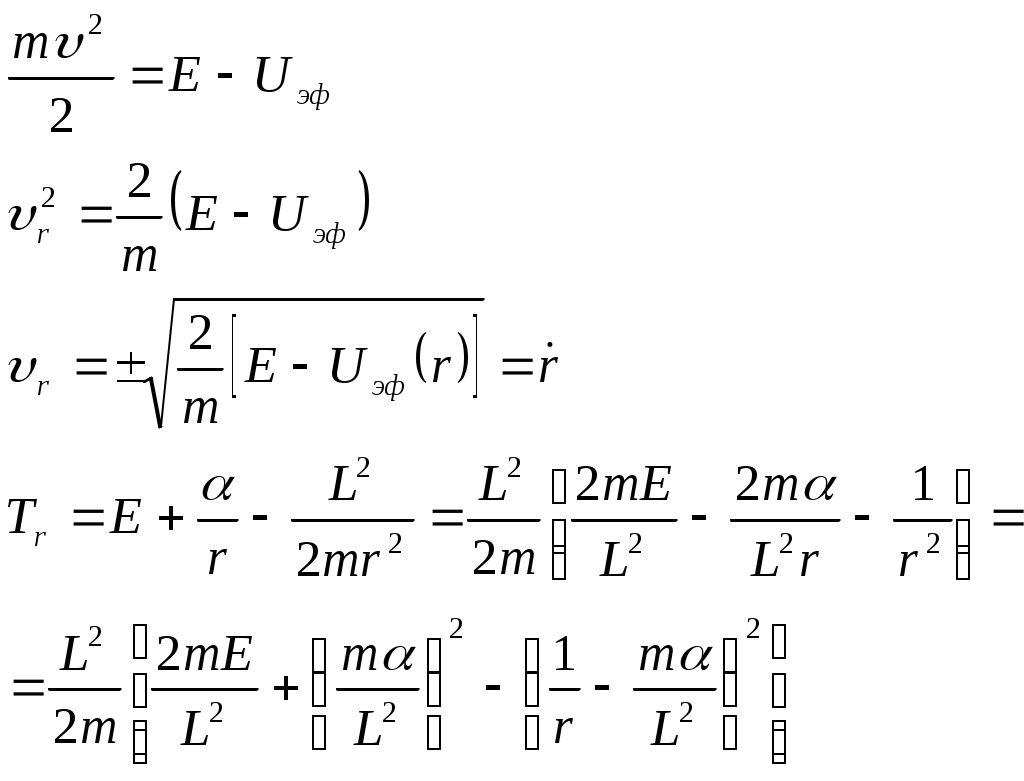 дополним до полного квадрата. дополним до полного квадрата.Введём диф. вел. 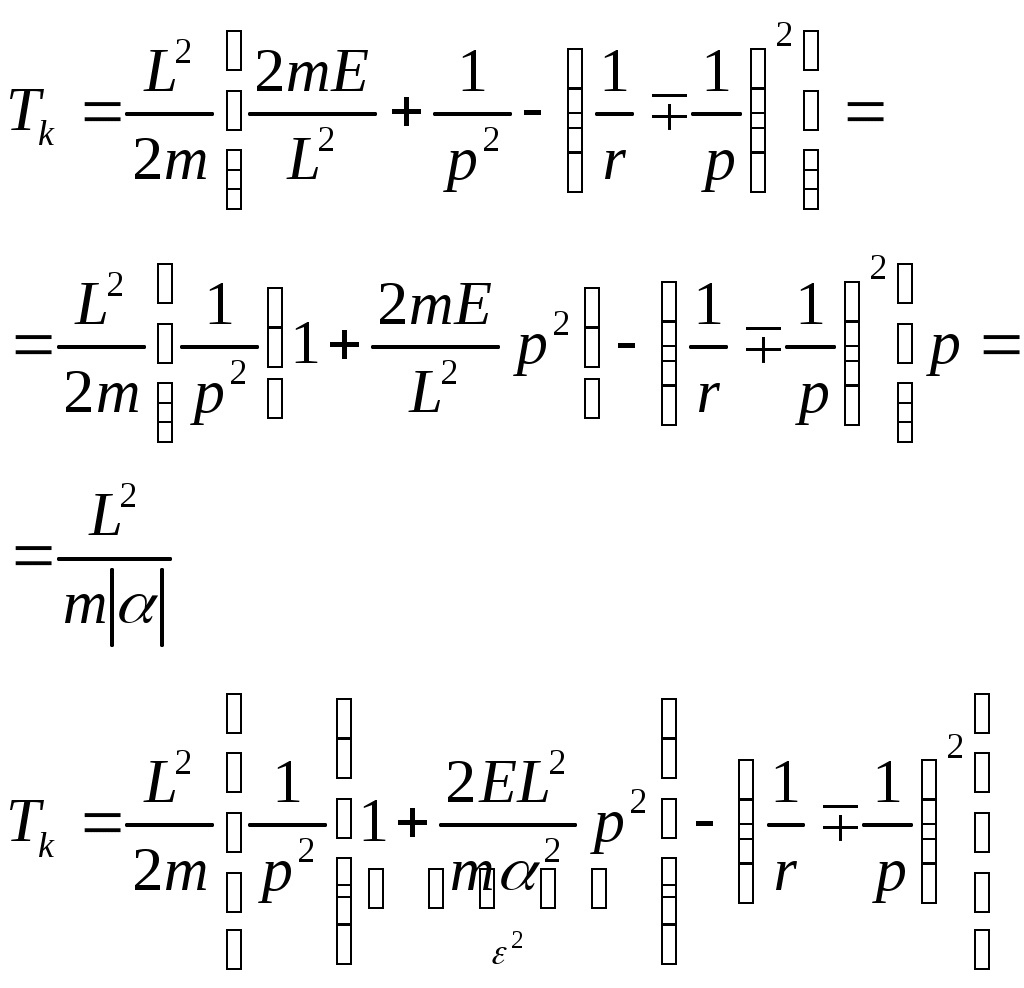 и 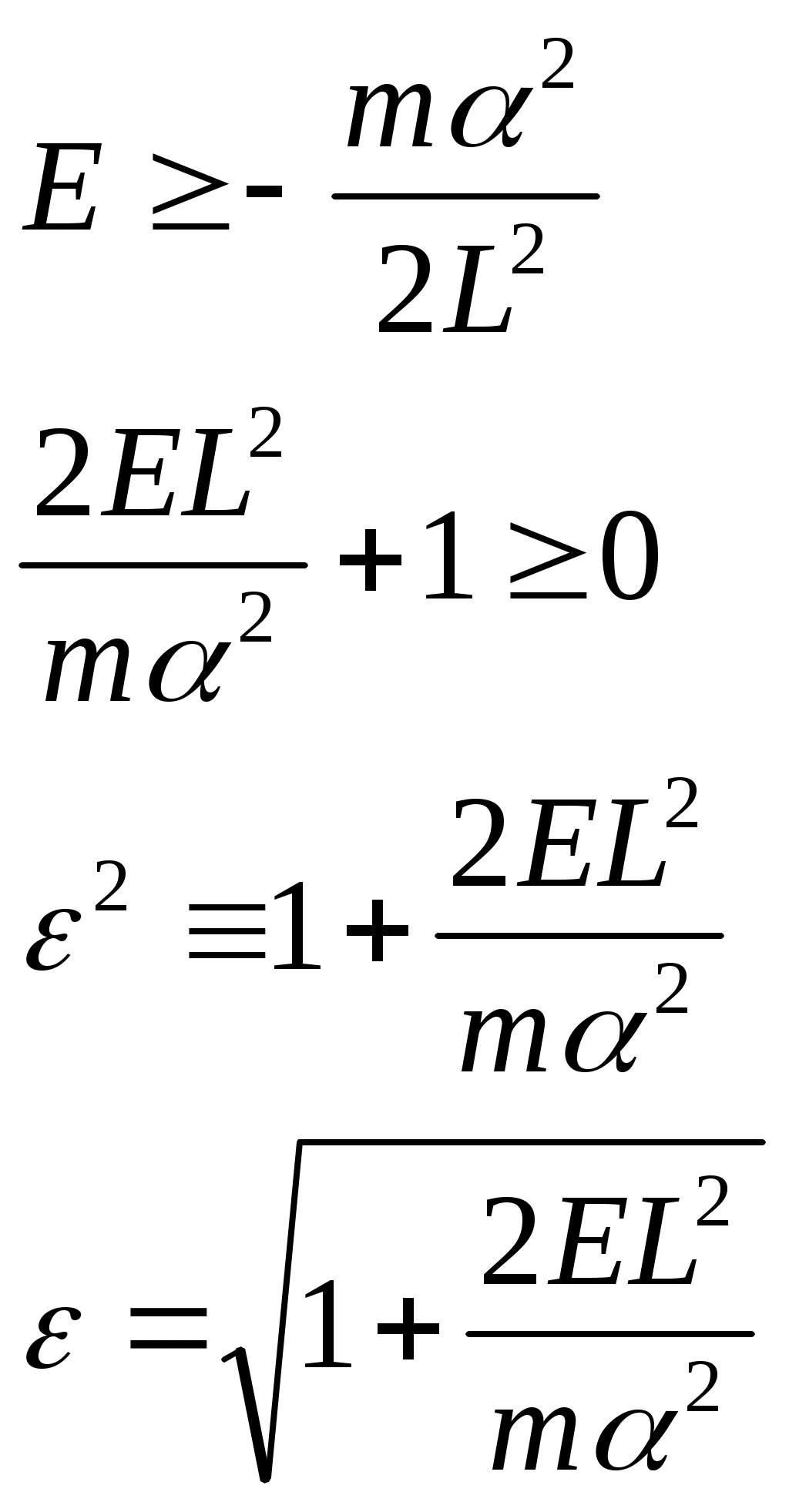 з-за усл. мин Е данн потенц вел положит. з-за усл. мин Е данн потенц вел положит.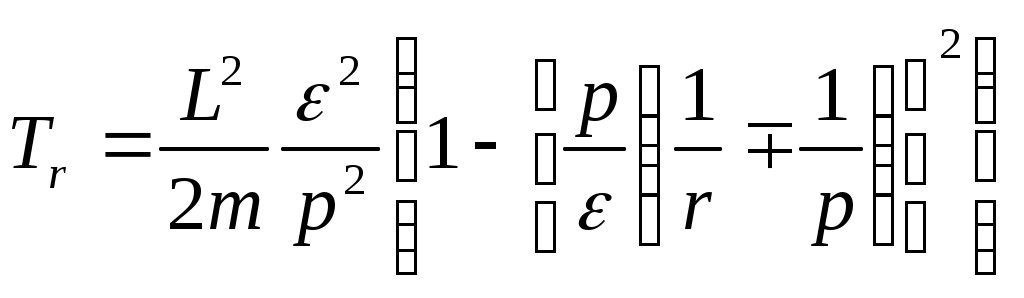 обозначим 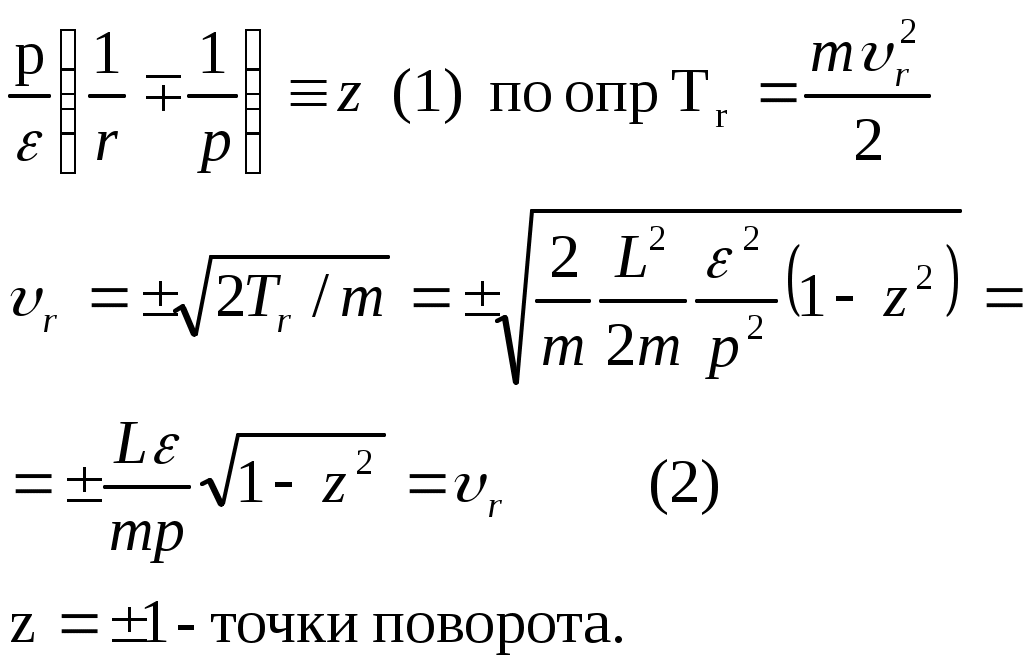 2.6 траектории в Кулоновском поле. В 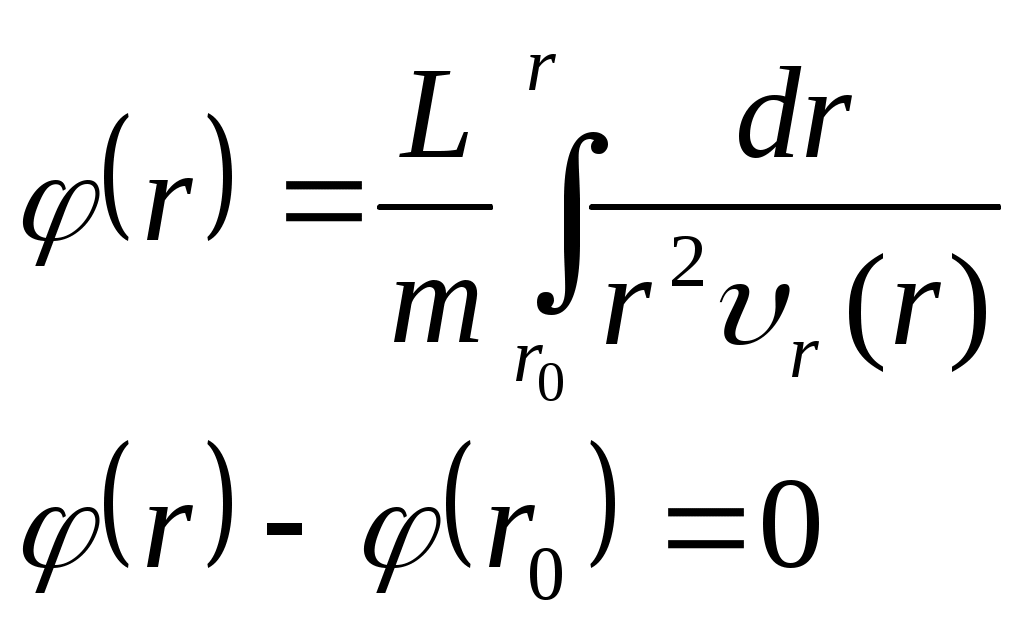 Пользуясь формулой п 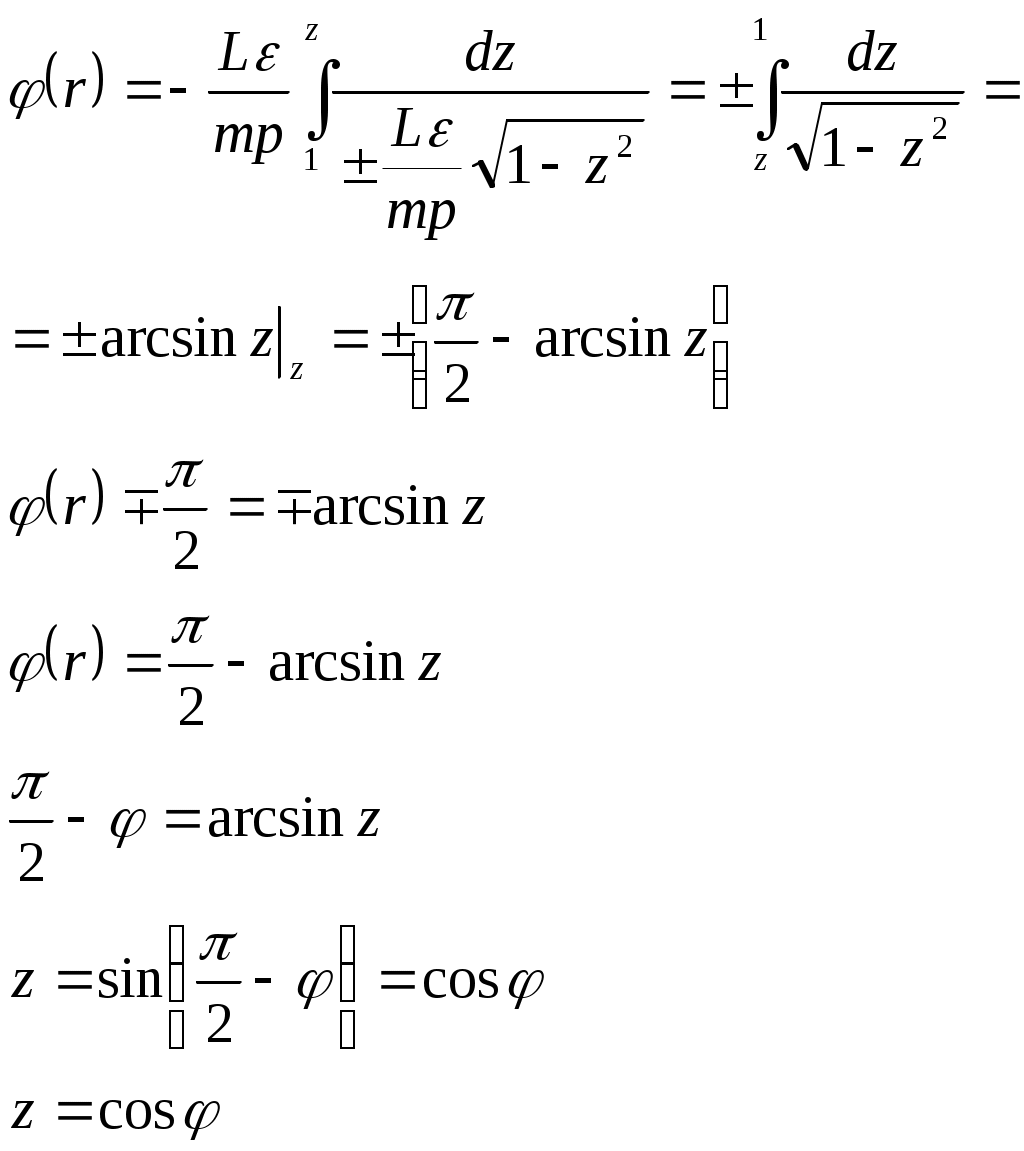 подставим z в 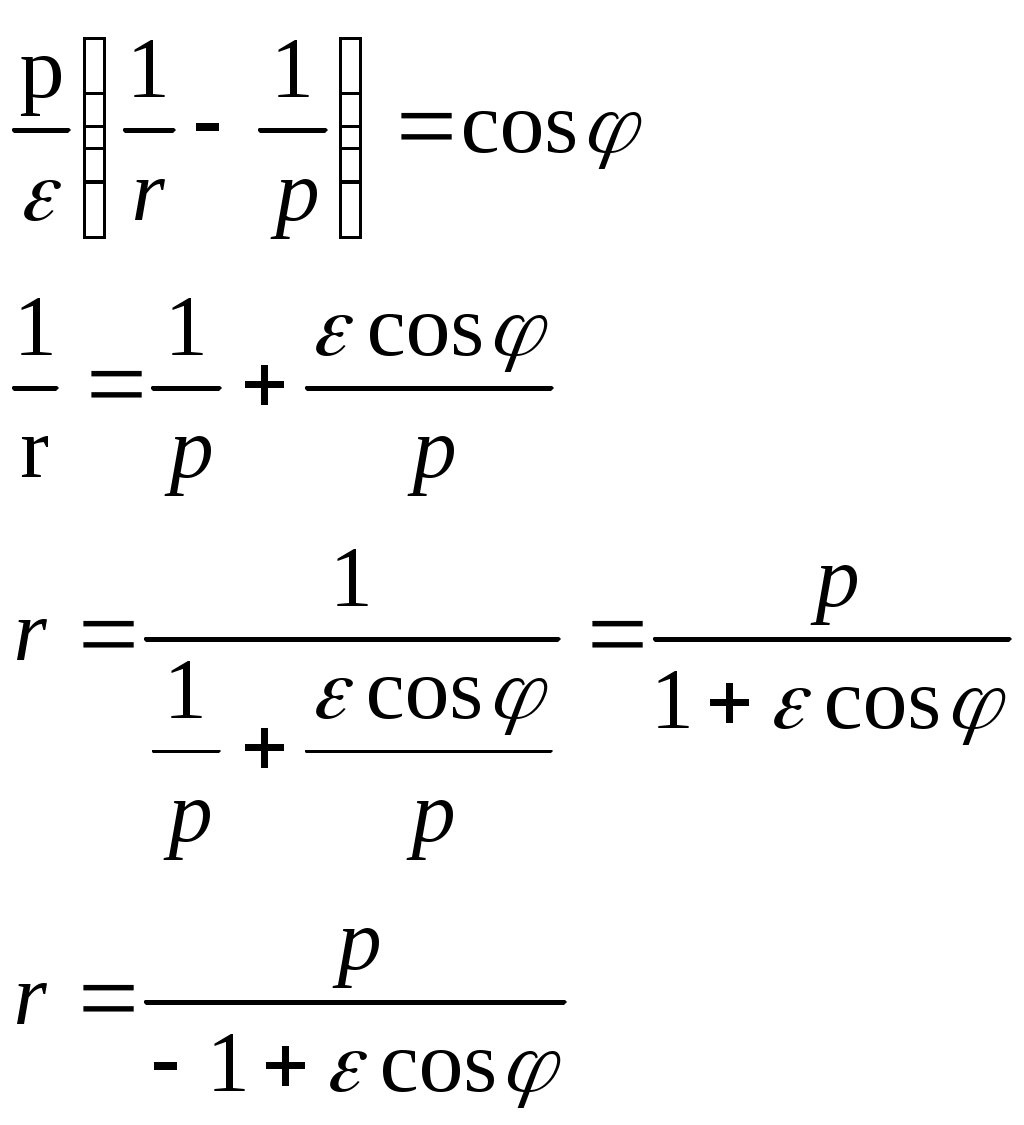 2.7. Классификация траекторий в кулоновском поле - П ε<1, то r<∞, E<0-финитное дв-е т 1 траект в поле притяж-я с полож энерг опис эллиптич траект. Если отр энерг , то парабол. Если Е=0, ε=1, то парабол. В случ отталкив-я всегда по гипербол траект 1 2 |
