15-16 сұрақ. Задача имеет только тривиальное решение Существование функции Грина докажем прямым построением функции Грина в виде
 Скачать 158.56 Kb. Скачать 158.56 Kb.
|
|
16 . Построение функции Грина, в случае, когда однородная задача имеет только тривиальное решение Существование функции Грина докажем прямым построением функции Грина в виде 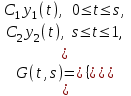 (3.1.6) (3.1.6)где  - решения следующих начальных задач: - решения следующих начальных задач:1) 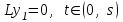 , , 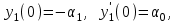 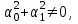 2) 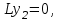 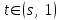 ; ; 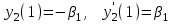 , , 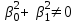 . .Заметим, что функции 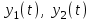 существуют согласно теореме существования и единственности решения задачи Коши и удовлетворяют однородным краевым условиям (3.1.2): существуют согласно теореме существования и единственности решения задачи Коши и удовлетворяют однородным краевым условиям (3.1.2):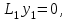 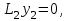 при этом, заметим, что 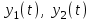 имеют производные до второго порядка включительно и эти производные непрерывны соответственно при имеют производные до второго порядка включительно и эти производные непрерывны соответственно при 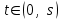 и и 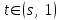 . .Функции 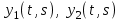 введены таким образом, что для функции (3.1.6) справедливы: введены таким образом, что для функции (3.1.6) справедливы:1) При 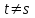 функция функция 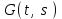 по переменной по переменной 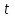 удовлетворяет однородному уравнению (3.1.1): удовлетворяет однородному уравнению (3.1.1): 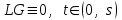 и и 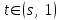 ; ;2) При 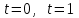 функция функция 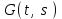 удовлетворяет граничным условиям (3.1.2): удовлетворяет граничным условиям (3.1.2):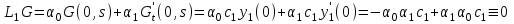 ; ;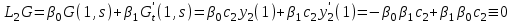 ; ;3) Функция 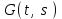 по переменной по переменной 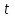 имеет частные производные до второго порядка включительно, и эти производные непрерывны при имеет частные производные до второго порядка включительно, и эти производные непрерывны при 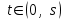 и и 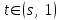 ; ;Осталось доказать, что можно подобрать 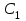 и и 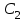 так, чтобы выполнялись условия сопряжения при так, чтобы выполнялись условия сопряжения при 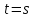 : : 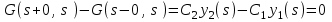 , ,(3.1.7) 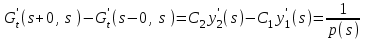 . . Здесь функции 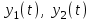 — линейно независимы. Если бы они были линейно зависимыми, то мы имели бы — линейно независимы. Если бы они были линейно зависимыми, то мы имели бы 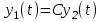 . Тогда бы выполнялось условие . Тогда бы выполнялось условие 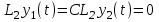 . Это означает, что . Это означает, что 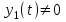 является решением однородной краевой задачи (3.1.1), (3.1.2). Пришли к противоречию, т. к., согласно условию, однородная краевая задача имеет только тривиальное решение. Следовательно, является решением однородной краевой задачи (3.1.1), (3.1.2). Пришли к противоречию, т. к., согласно условию, однородная краевая задача имеет только тривиальное решение. Следовательно, 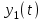 и и 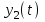 линейно независимы, и их определитель Вронского не равен нулю. Причем, согласно теореме 1.3.1 имеем линейно независимы, и их определитель Вронского не равен нулю. Причем, согласно теореме 1.3.1 имеем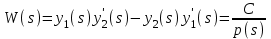 (3.1.8) (3.1.8) С другой стороны определитель Вронского 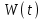 является и определителем системы (3.1.7), то находим является и определителем системы (3.1.7), то находим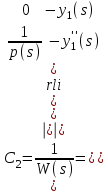 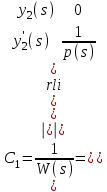 Подставляя эти значения в (3.1.6), получаем функцию Грина в виде 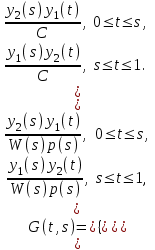 (3.1.9) (3.1.9)где С находится согласно (3.1.8). Легко видеть, что 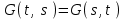 . Таким образом, доказано существование и единственность функции Грина для случая, когда однородная задача имеет только тривиальное решение. . Таким образом, доказано существование и единственность функции Грина для случая, когда однородная задача имеет только тривиальное решение.Пример 3.1.1. Докажите, что однородная краевая задача 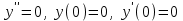 (3.1.10) (3.1.10)имеет лишь тривиальное решение 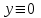 . .Решение. Интегрируя уравнение 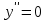 , получаем , получаем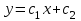 . (3.1.11) . (3.1.11)Подставляя (3.1.11) в краевые условия (3.1.10), находим, что 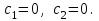 С учетом этих значений функция (3.1.11) примет вид С учетом этих значений функция (3.1.11) примет вид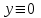 . .Следовательно, краевая задача (3.1.10) имеет лишь тривиальное решение. Пример 3.1.2. Для краевой задачи 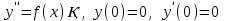 (3.1..12) (3.1..12)построите функцию Грина. Решение. Соответствующая однородная краевая задача согласно примеру 3.1.1 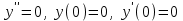 имеет лишь тривиальное решение 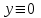 . Следовательно, для краевой задачи (3.1.12) существует единственная функция Грина . Следовательно, для краевой задачи (3.1.12) существует единственная функция Грина 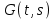 . .Теперь, используя свойства функции Грина для искомой функции 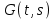 , получим задачу: , получим задачу: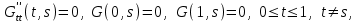 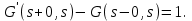 Интегрируя уравнение 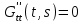 один раз, находим один раз, находим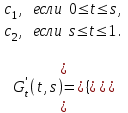 Здесь, 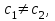 так как по условию производная так как по условию производная 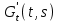 терпит разрыв при терпит разрыв при 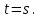 Далее, интегрируя Далее, интегрируя 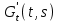 , получаем , получаем 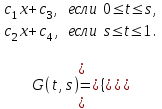 (3.1.13) (3.1.13) Поскольку функция 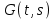 по определению непрерывна, то должно выполняться условие по определению непрерывна, то должно выполняться условие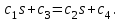 (3.1.14) (3.1.14)Из краевых условий (1.8.10) для функции 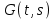 последует, что последует, что 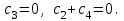 (3.1.15) (3.1.15)Условия скачка производной при 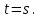 приобретает вид приобретает вид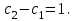 (3.1.16) (3.1.16)Решив систему (3.1.14)-( 3.1.16) относительно 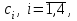 получим получим 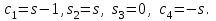 Подставив эти значения в (3.1.13), находим функцию Грина 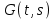 для краевой задачи (3.1.12): для краевой задачи (3.1.12):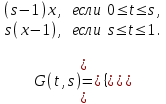 Пример 3.1.3. Докажите, что самосопряженная однородная краевая задача 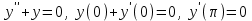 (3.1.17) (3.1.17)имеет лишь тривиальное решение 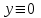 . Для этой задачи построите функцию Грина. . Для этой задачи построите функцию Грина.Решение. Общее решение однородного дифференциального уравнения (3.1.17) выглядит следующим образом: 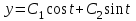 . (3.1.18) . (3.1.18)Подставляя (3.1.18) в краевые условия (3.1.17), получаем систему уравнений: 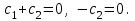 Отсюда и из (3.1.18) следует, что однородная краевая задача (3.1.12) имеет только лишь тривиальное решение 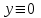 . . 15. Докажите существование функции Грина в случае, когда однородная задача имеет только тривиальное решение. Существование функции Грина докажем прямым построением функции Грина. Решая уравнение 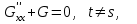 имеем имеем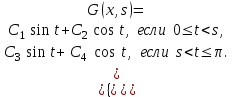 Из краевых условий для функции 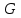 получаем: получаем: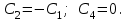 . . Отсюда, находим: 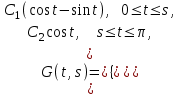 (3.1.19) (3.1.19)Поскольку функция 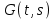 по определению непрерывна, то должно выполняться условие по определению непрерывна, то должно выполняться условие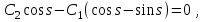 (3.1.20) (3.1.20)Условия скачка производной при 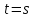 приобретает вид приобретает вид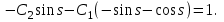 (3.1.21) (3.1.21)Решив систему уравнений (3.1.20), (3.1.21), находим 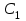 и и 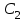 : :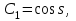 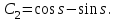 Подставляя эти значения в (3.1.19), получаем функцию 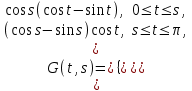 (3.1.22) (3.1.22)Легко видеть что, 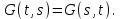 Построенная таким образом функция по построению удовлетворяет 3)-4) условиям функции Грина. Теперь покажем, что функция Построенная таким образом функция по построению удовлетворяет 3)-4) условиям функции Грина. Теперь покажем, что функция 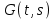 удовлетворяет условиям 1)-2): удовлетворяет условиям 1)-2):1) При 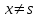 функция функция 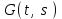 по переменной по переменной 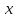 удовлетворяет однородному уравнению (3.1.17): удовлетворяет однородному уравнению (3.1.17): 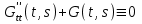 при при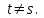 Действительно, определив 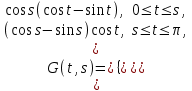 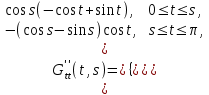 отсюда заключаем, что функция 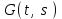 удовлетворяет однородному уравнению (3.1.17) при удовлетворяет однородному уравнению (3.1.17) при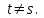 2) При 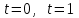 построенная функция построенная функция 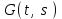 удовлетворяет граничным условиям (3.1.17): удовлетворяет граничным условиям (3.1.17):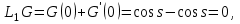 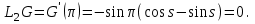 Таким образом, построенная функция (3.1.22) является функцией Грина. |
