Задача. Задача Имеются данные о стоимости основных фондов и выпуске продукции десяти предприятий, млн руб
 Скачать 129.5 Kb. Скачать 129.5 Kb.
|
Задачи к теме 9ЗадачаИмеются данные о стоимости основных фондов и выпуске продукции десяти предприятий, млн руб.:
Выявите наличие, направление и форму связи между выпуском продукции и стоимостью основных фондов, используя графический метод и метод сопоставления параллельных рядов. Представьте связь в виде уравнения регрессии, проанализируйте параметры уравнения регрессии и оцените тесноту связи. Сделайте выводы. Решение Корреляционную зависимость для наглядности можно изобразить графически. Для этого, имея 10 взаимосвязанных пар значений x и y и пользуясь прямоугольной системой координат, каждую такую пару изображают в виде точки на плоскости с координатами x и y(рис.1.) 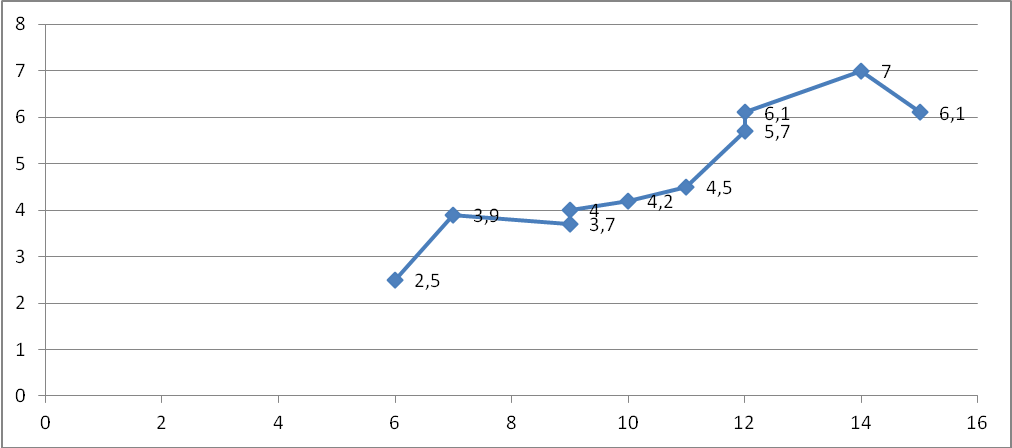 Рис.1. Графический метод Соединяя последовательно нанесенные точки, получают ломаную линию, именуемую эмпирической линией регрессии. В нашей задаче эта линия похожа на восходящую прямую, что позволяет выдвинуть гипотезу о наличии прямой зависимости между величиной основных фондов и валовым выпуском продукции. Метод сопоставления параллельных рядов. Единицы наблюдения располагают по возрастанию значений факторного признака х и затем сравнивают с ним (визуально) поведение результативного признака у. В нашей задаче в большинстве случаев по мере увеличения значений x увеличиваются и значения y 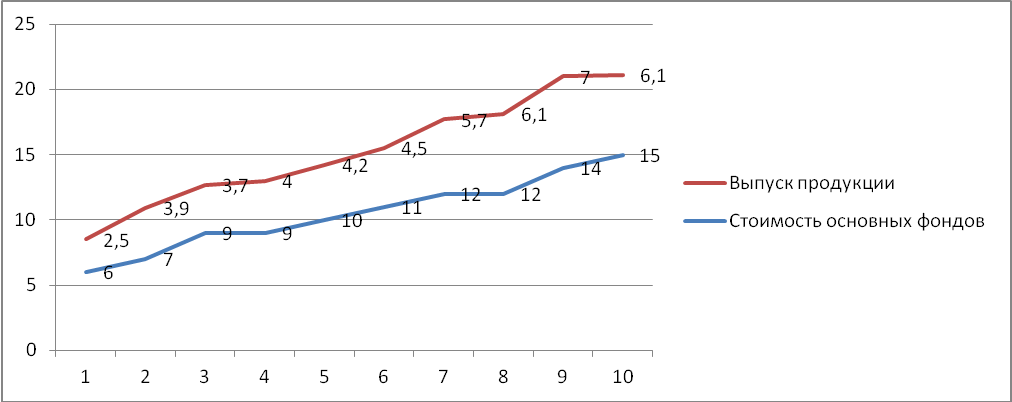 Рис.2. Метод сопоставления параллельных рядов На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер. Линейное уравнение регрессии имеет вид y = bx + a Оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок εi, a и b соответственно оценки параметров α и β регрессионной модели. Можно говорить о прямой связи между х и у (этот вывод подтверждает и эмпирическая линия регрессии). Теперь необходимо ее измерить, для чего рассчитывают несколько коэффициентов. Уравнение парной регрессии. Для расчета параметров регрессии построим расчетную таблицу (табл. 1) Таблица 1 –Расчетная таблица определения параметров регрессии
Для наших данных система уравнений имеет вид 10a + 105·b = 47.7 105·a + 1177·b = 534.2 Домножим уравнение (1) системы на (-10.5), получим систему, которую решим методом алгебраического сложения. -105a -1102.5 b = -500.85 105*a + 1177*b = 534.2 Получаем: 74.5*b = 33.35 Откуда b = 0.4477 Теперь найдем коэффициент «a» из уравнения: 10a + 105*b = 47.7 10a + 105*0.4477 = 47.7 10a = 0.697 a = 0.06966 Получаем эмпирические коэффициенты регрессии: b = 0.4477, a = 0.06966 Уравнение регрессии (эмпирическое уравнение регрессии): y = 0.4477 x + 0.06966 Эмпирические коэффициенты регрессии a и b являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных. 1. Параметры уравнения регрессии. Выборочные средние. Выборочные дисперсии: = Среднеквадратическое отклонение Коэффициент корреляции b можно находить по формуле, не решая систему непосредственно: Коэффициент корреляции. Ковариация. Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле: Линейный коэффициент корреляции принимает значения от –1 до +1. Связи между признаками могут быть слабыми и сильными (тесными). 0.1 < rxy < 0.3: слабая; 0.3 < rxy < 0.5: умеренная; 0.5 < rxy < 0.7: заметная; 0.7 < rxy < 0.9: высокая; 0.9 < rxy < 1: весьма высокая; В нашем примере связь между признаком Y и фактором X высокая и прямая. Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии b: Уравнение регрессии (оценка уравнения регрессии). = Линейное уравнение регрессии имеет вид y = 0.448 x + 0.0697 Связь между у и х определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе - обратная). В нашем примере связь прямая. Для оценки качества параметров регрессии построим расчетную таблицу (табл. 2) Таблица 2 - Расчетная таблица оценки параметров регрессии
Анализ точности определения оценок коэффициентов регрессии. Несмещенной оценкой дисперсии возмущений является величина: S2 = 0.311 - необъясненная дисперсия или дисперсия ошибки регрессии (мера разброса зависимой переменной вокруг линии регрессии). S = 0.56 - стандартная ошибка оценки. Стандартная ошибка регрессии рассматривается в качестве меры разброса данных наблюдений от смоделированных значений. Чем меньше значение стандартной ошибки регрессии, тем качество модели выше. Sa - стандартное отклонение случайной величины a. Sb - стандартное отклонение случайной величины b. Таким образом, в работе изучена зависимость Y от X. На этапе спецификации была выбрана парная линейная регрессия. Оценены её параметры методом наименьших квадратов. Статистическая значимость уравнения проверена с помощью коэффициента детерминации. Установлено, что в исследуемой ситуации 85.7% общей вариабельности Y объясняется изменением X. Установлено также, что параметры модели статистически не значимы. Возможна экономическая интерпретация параметров модели - увеличение X (основных фондов предприятия) на 1 ед.изм. приводит к увеличению Y в среднем на 0.448 ед.изм. (объем выпуска продукции) Список литературы Баврин И.И. Теория вероятностей и математическая статистика / И.И.Баврин. - М.: Высш. шк., 2005.— 160 с: Вентцель Е. С. Задачи и упражнения по теории вероятностей: Учеб. пособие для студ. втузов / Е. С. Вентцель, Л. А. Овчаров. — 5-е изд., испр. — М.: Издательский центр «Академия», 2003. — 448 с. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике /В. Е. Гмурман. - М., Высш.шк., 2004.- 404 с. Гнеденко Б.В. Курс теории вероятностей: Учебник / Б.В. Гнеденко. - Изд. 8-е, испр. и доп. — М.: Едиториал УРСС, 2005. — 448 с. Математическая статистика: Учеб. для вузов / В. Б. Горяинов, И. В. Павлов, Г. М. Цветкова, О. И. Тескин.; Под ред. B.C. Зарубина, А.П. Крищенко. - М.: Иэд-во МГТУ им. Н.Э. Баумана, 2001. 424 с. |
