СОДЕРЖАНИЕ
1. Задача интерполяции.
Когда теоретических знаний оказывается недостаточно для построения математической модели, можно воспользоваться данными эксперимента – наблюдениями за его функционированием.
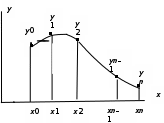
Пусть известна математическая модель 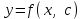 с точностью до параметров с точностью до параметров 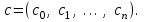 Необходимо найти функцию, проходящую через точки Необходимо найти функцию, проходящую через точки  где где 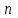 – число экспериментов (Рисунок 1). – число экспериментов (Рисунок 1).
Рисунок 1 – Исходные данные в задаче интерполяции
Для этого должно выполняться условие Лагранжа:
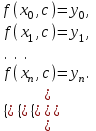 (1.1) (1.1)
Если число параметров функции  совпадает с числом узлов совпадает с числом узлов 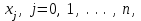 система (1.1) может иметь решение; в этом случае говорят о задаче интерполяции. система (1.1) может иметь решение; в этом случае говорят о задаче интерполяции.
Для целей интерполяции обычно используется полином:
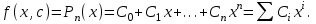
Условие Лагранжа дает следующую систему линейных алгебраических уравнений для определения коэффициентов интерполяции 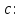
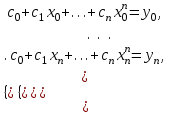 (1.2) (1.2)
или
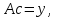
где 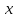 −вектор узлов интерполяции −вектор узлов интерполяции 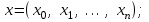 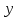 – вектор значенийфункции в узлах интерполяции – вектор значенийфункции в узлах интерполяции 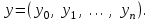
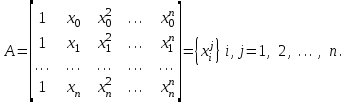
Решение системы (1.2) дает значение коэффициентов 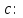
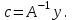
Полученное уравнение кривой проходит точно через заданные точки. Вне узлов интерполяции математическая модель может иметь значительную погрешность.
Рассмотрим применение приведенных выше теоретических материалов на примере решения задачи в программе MATHCAD.
Условия задачи: найти интерполяционный полином с узлами 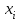 , расположенными равномерно на отрезке [0,1] c шагом 0,1 и значениями , расположенными равномерно на отрезке [0,1] c шагом 0,1 и значениями  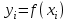 . Вычислить ошибку интерполяции в узлах с шагом 0,05. Результат представить в виде графиков. . Вычислить ошибку интерполяции в узлах с шагом 0,05. Результат представить в виде графиков.
Исходные данные: 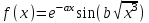 , где a = 1,4, b = 1,9. , где a = 1,4, b = 1,9.
На рисунке 2 приведено решение задачи интерполяции в программе MATHCAD.
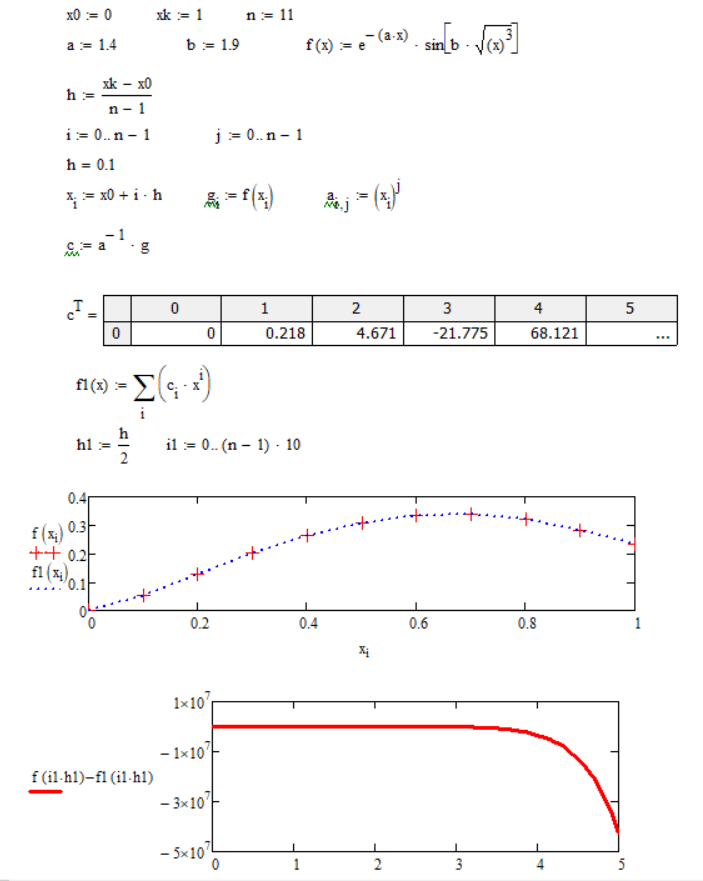
Рисунок 2 – Решение задачи интерполяции в программе MATHCAD
2. Аппроксимация функций
При большом числе измерений и при наличии помех задача интерполяции становится бессмысленной. Далее будем предполагать известной математическую модель с точностью до констант 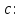
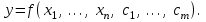
Пусть имеются данные эксперимента для входных переменных 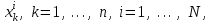 где где 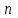 − размерность вектора − размерность вектора 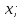 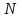 – число экспериментов и соответствующие значения выходной переменной – число экспериментов и соответствующие значения выходной переменной 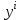 в эксперименте в эксперименте 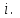 Подставляя эти числовые данные в уравнение для модели, получим систему уравнений Подставляя эти числовые данные в уравнение для модели, получим систему уравнений
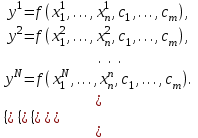
При 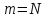 получим систему уравнений для определения параметров получим систему уравнений для определения параметров 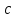 в задаче интерполяции, и модель будет проходить точно через экспериментальные точки. Однако для проверки соответствия модели реальности никакой информации иметь не будем. Если в задаче интерполяции, и модель будет проходить точно через экспериментальные точки. Однако для проверки соответствия модели реальности никакой информации иметь не будем. Если 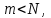 то число условий избыточно и выбором то число условий избыточно и выбором 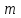 параметров вектора параметров вектора 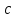 удовлетворить всем удовлетворить всем 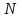 условиям не сможем. условиям не сможем.
Теперь сформулируем функцию невязки между экспериментальными данными и предсказанными по модели в виде нормы
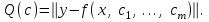
Наиболее часто используют квадратичную норму:  (2.1) (2.1)
и минимизация этой ошибки приводит к процедуре решения уравнения (2.1) методом наименьших квадратов. В общем случае минимизация Q может быть осуществлена лишь численно.
Для достаточно широкого класса задач минимизацию функции невязки можно осуществить аналитически. Такой класс составляют функции, линейные по параметрам 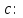
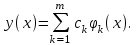
Для такой модели
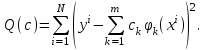
Условие минимума функции:
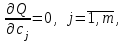
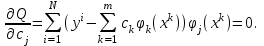
Раскрывая скобки и меняя порядок суммирования, получим
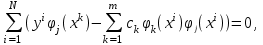
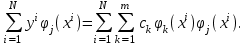
Введем следующие обозначения:
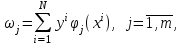
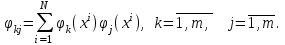
Тогда можно записать систему линейных уравнений

или, в векторном виде,
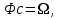
где 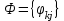 − информационная матрица. − информационная матрица.
Решение этой системы
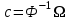
дает искомые значения параметров модели.
Для случая линейной модели, зависящей от n переменных, имеем:
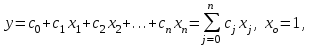
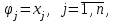
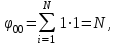
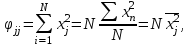

Для произвольных j и k, jk
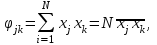
где через 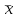 обозначено среднее значение величины обозначено среднее значение величины 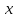 . .
Для модели 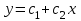 нужно провести прямую, наименьшим образомуклоняющуюся от точек с координатами нужно провести прямую, наименьшим образомуклоняющуюся от точек с координатами 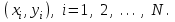 В этом случае В этом случае
 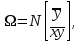
и нужно решить систему уравнений
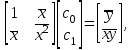
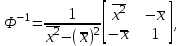
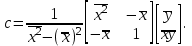
В случае аппроксимации исходных данных полиномом
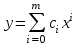
имеем следующую структуру матрицы 
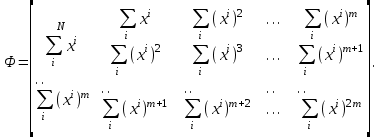
По данным задачи, приведенным ранее, найдем аппроксимирующий полином второго порядка. На рисунке 3 представлено решение задания в программе MATHCAD.
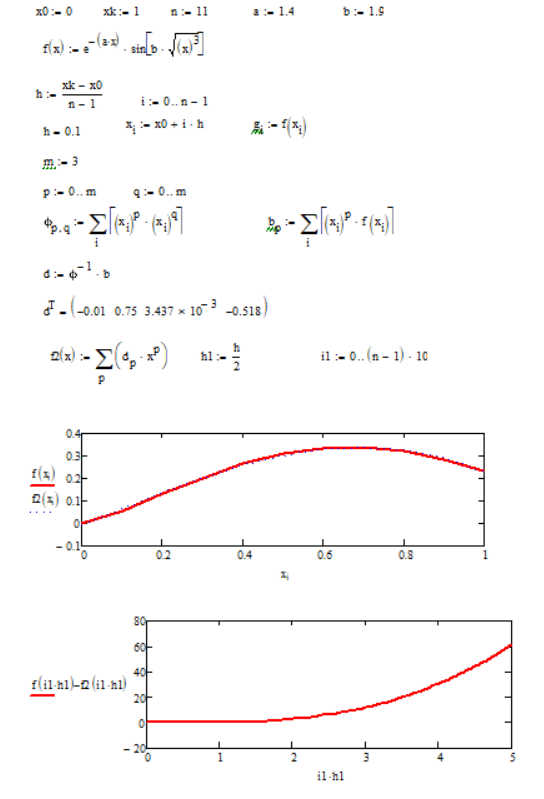
Рисунок 3 – Решение задачи аппроксимации в программе MATHCAD
3. Метод простой итерации
Пусть дано уравнение с одной неизвестной переменной x
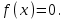 (3.1) (3.1)
Приведем (3.1) к виду
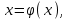 (3.2) (3.2)
разрешая (3.1) по x или принимая 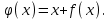
Уравнения (3.1) или (3.2) могут иметь много решений, одно решение либо вообще не иметь решений.
Влиять на сходимость можно в определенной мере введением итерационного параметра . Для этого уравнение (3.1) представим в виде
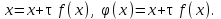 (3.3) (3.3)
Теперь на функцию 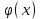 можно влиять выбором параметра можно влиять выбором параметра 
Рассмотрим итерационный процесс для уравнения
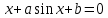 , ,
где 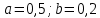 ; ;  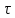 =-0,5. =-0,5.
Применим метод простой интеграции. Результат представлен на рисунке 4.
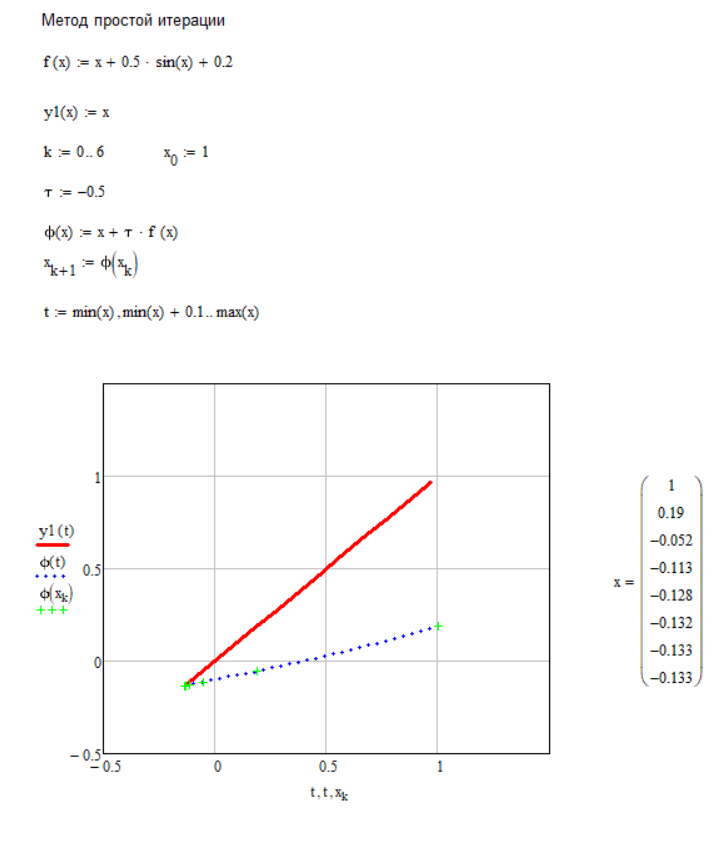 Рисунок 4 – Решение нелинейного уравнения методом простой итерации Рисунок 4 – Решение нелинейного уравнения методом простой итерации
В случае решения систем нелинейных уравнений
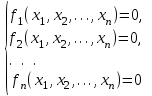 (3.4) (3.4)
формально итерационный процесс описывается теми же соотношениями, что и в скалярном случае. Систему (3.4) в векторной форме можно записать в виде
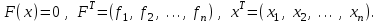
Тогда итерационная схема будет иметь следующий вид:
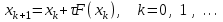
4. Метод Ньютона
В методе простой итерации значение итерационного параметра 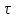 всегда остается постоянным. Метод Ньютона позволяет улучшить сходимость метода за счет надлежащего выбора этого параметра на каждом шаге итерационного процесса. всегда остается постоянным. Метод Ньютона позволяет улучшить сходимость метода за счет надлежащего выбора этого параметра на каждом шаге итерационного процесса.
Рассмотрим скалярное уравнение (3.1) 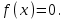
При рассмотрении метода простой итерации установлено влияние на сходимость итерационного процесса параметра . Метод Ньютона позволяет определить в некотором смысле наилучшие значения итерационного параметра. Цена этого определения – использование не только значений функции 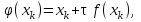 но и производной но и производной 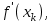 что требует непрерывности и функции и ее производной. что требует непрерывности и функции и ее производной.
Выражение для итерационного параметра
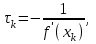
и итерационного процесса Ньютона

Обобщим метод Ньютона для системы нелинейных уравнений:
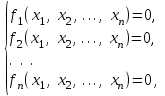
или, в векторном виде, 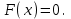
Матрица первых производных (матрица Якоби)

Итерационный процесс Ньютона
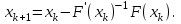
Рассмотрим итерационный процесс для уравнения
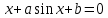 , ,
где 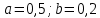 ; ; 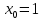 . .
Применим метод Ньютона в программе MATHCAD. Результат представлен на рисунке 5.
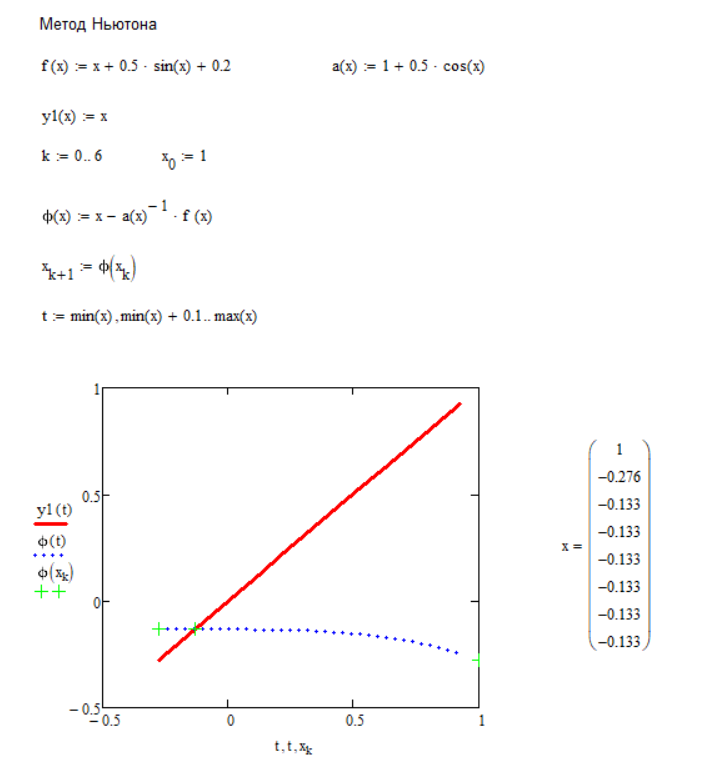
Рисунок 5 – Решение нелинейного уравнения методом Ньютона
Вывод по практической работе
В ходе практической работы № 4 мы изучили теорию для решения задач интерполяции и аппроксимации функций, и для решения уравнений методом простой интеграции и методом Ньютона. А также применили полученные знания на практике при решении заданий с помощью программы MATHCAD. |
 Скачать 415.54 Kb.
Скачать 415.54 Kb.
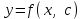 с точностью до параметров
с точностью до параметров 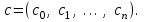 Необходимо найти функцию, проходящую через точки
Необходимо найти функцию, проходящую через точки  где
где 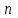 – число экспериментов (Рисунок 1).
– число экспериментов (Рисунок 1).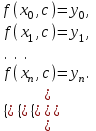 (1.1)
(1.1) совпадает с числом узлов
совпадает с числом узлов 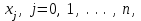 система (1.1) может иметь решение; в этом случае говорят о задаче интерполяции.
система (1.1) может иметь решение; в этом случае говорят о задаче интерполяции.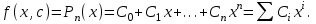
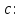
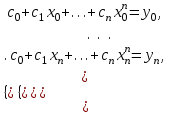 (1.2)
(1.2)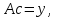
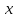 −вектор узлов интерполяции
−вектор узлов интерполяции 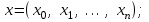
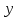 – вектор значенийфункции в узлах интерполяции
– вектор значенийфункции в узлах интерполяции 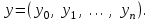
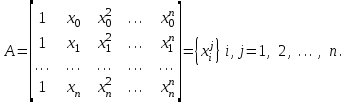
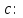
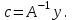
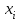 , расположенными равномерно на отрезке [0,1] c шагом 0,1 и значениями
, расположенными равномерно на отрезке [0,1] c шагом 0,1 и значениями 
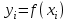 . Вычислить ошибку интерполяции в узлах с шагом 0,05. Результат представить в виде графиков.
. Вычислить ошибку интерполяции в узлах с шагом 0,05. Результат представить в виде графиков.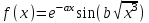 , где a = 1,4, b = 1,9.
, где a = 1,4, b = 1,9.
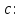
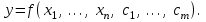
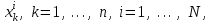 где
где 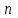 − размерность вектора
− размерность вектора 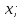
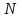 – число экспериментов и соответствующие значения выходной переменной
– число экспериментов и соответствующие значения выходной переменной 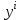 в эксперименте
в эксперименте 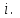 Подставляя эти числовые данные в уравнение для модели, получим систему уравнений
Подставляя эти числовые данные в уравнение для модели, получим систему уравнений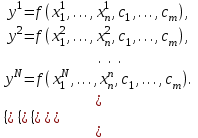
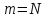 получим систему уравнений для определения параметров
получим систему уравнений для определения параметров 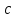 в задаче интерполяции, и модель будет проходить точно через экспериментальные точки. Однако для проверки соответствия модели реальности никакой информации иметь не будем. Если
в задаче интерполяции, и модель будет проходить точно через экспериментальные точки. Однако для проверки соответствия модели реальности никакой информации иметь не будем. Если 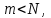 то число условий избыточно и выбором
то число условий избыточно и выбором 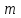 параметров вектора
параметров вектора 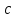 удовлетворить всем
удовлетворить всем 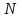 условиям не сможем.
условиям не сможем.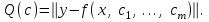


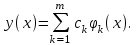
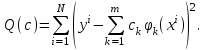
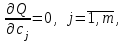
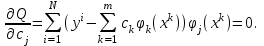
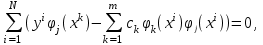
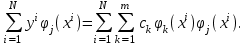
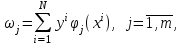
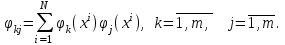

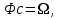
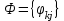 − информационная матрица.
− информационная матрица.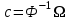
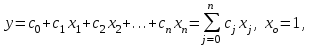
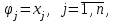
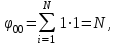
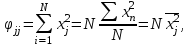

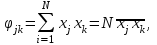
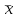 обозначено среднее значение величины
обозначено среднее значение величины 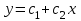 нужно провести прямую, наименьшим образомуклоняющуюся от точек с координатами
нужно провести прямую, наименьшим образомуклоняющуюся от точек с координатами 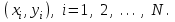 В этом случае
В этом случае
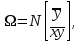
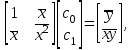
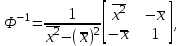
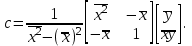
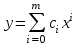

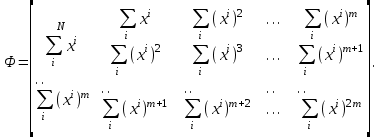

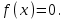 (3.1)
(3.1)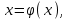 (3.2)
(3.2)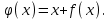
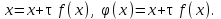 (3.3)
(3.3)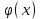 можно влиять выбором параметра
можно влиять выбором параметра 
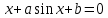 ,
,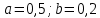 ;
; 
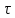 =-0,5.
=-0,5.
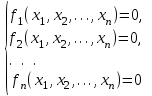 (3.4)
(3.4)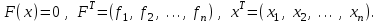
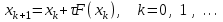
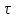 всегда остается постоянным. Метод Ньютона позволяет улучшить сходимость метода за счет надлежащего выбора этого параметра на каждом шаге итерационного процесса.
всегда остается постоянным. Метод Ньютона позволяет улучшить сходимость метода за счет надлежащего выбора этого параметра на каждом шаге итерационного процесса.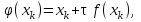 но и производной
но и производной 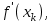 что требует непрерывности и функции и ее производной.
что требует непрерывности и функции и ее производной. 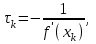

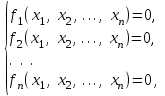
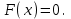

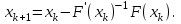
 .
.