Задача 1. Линейные электрические цепи постоянного тока.. Задача Линейные электрические цепи постоянного тока. E1, В e2, В
 Скачать 201.5 Kb. Скачать 201.5 Kb.
|
|
Определить количество узлов и ветвей в схеме, обозначить узлы (a, b, c …) и условно положительные направления токов в ветвях схемы и напряжений на ее участках. Определить: • токи во всех ветвях схемы, расчет произвести методом контурных токов, выполнить проверку правильности расчета методом баланса мощностей; • токи во всех ветвях схемы (I1-I5), исключив ветвь с сопротивлением R6. Расчет произвести методом наложения. Задача 1. Линейные электрические цепи постоянного тока.
Рисунок вариант 2: 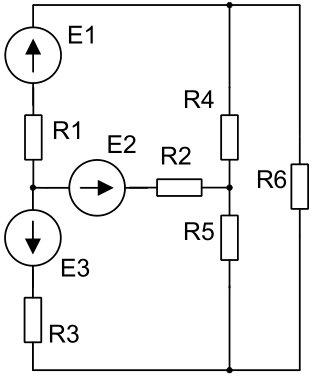 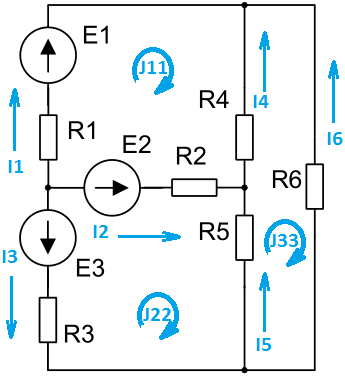 Решение Запишем уравнения, используя метод контурных токов: J11*(R1+R2+R4)-J22*R2-J33*R4=E1-E2 J22*(R2+R3+R5)-J11*R2-J33*R5= E2-E3 J33*(R4+R5+R6)-J11*R4-J22*R5= 0 После подстановки данных получаем систему уравнений: 1 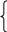 30J11 - 40J22 - 40J33 =10 30J11 - 40J22 - 40J33 =10- 40J11+160J22 - 40J33 =-50 - 40J11 - 40J22+180J33= 0 Решение системы находим методом Крамера: 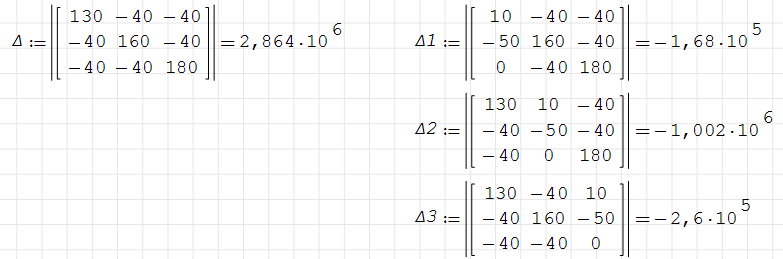 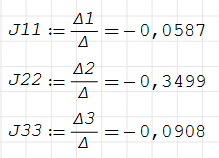 Истинные токи в ветвях равны: I1 = J11= - 0.0587А; I2= J22 – J11= - 0.2912 А; I3= - J22= 0.3499 А; I4 = J33 – J11= - 0.0321 А; I5 = J33 – J22= 0.5667 А; I6= – J33= 0.0908 А; Проверим баланс мощности. Вычислим мощность источников и мощность потребителей. Сравнивая результаты, убеждаемся, что баланс мощностей выполняется. Таким образом, токи равны: I1 = - 0.0587А; I2= - 0.2912 А; I3=0.3499 А; I4 = - 0.0321 А; I5 = 0.5667 А; I6= 0.0908 А; (знак ‘ – ‘ означает, что действительное направление тока противоположно выбранному на схеме) По условию задания обрываем ветвь с резистором R6 и находим токи в ветвях. Для этого применяем метод наложения. 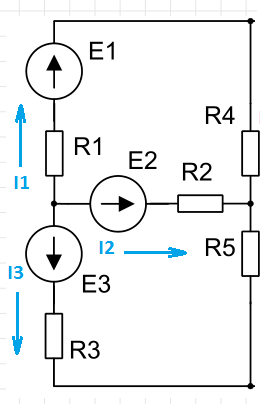  Схема имеет три ветви с токами I1, I2, I3. Рассмотрим три схемы. В первой их них источники ЭДС Е2 и Е3 заменяем перемычкой, токи в схеме обозначим Í1, Í́́ 2, Í́́ 3 Во второй схеме источники ЭДС Е1 и Е3 заменяем перемычкой, токи в схеме обозначим Í́ ́1, Í́́ ́2, Í́́ ́3 В третьей схеме источники ЭДС Е1 и Е2 заменяем перемычкой, токи в схеме обозначим Í́́ ́ ́1, Í́́ ́ ́2, Í́́ ́ ́3 Токи находим любым способом, например, по законам Кирхгофа Для первой схемы: -  Í1 - Í́́ 2 -Í́́ 3=0 Í1 - Í́́ 2 -Í́́ 3=0Í1(R1+R4)- Í2R2=E1 Í2R2 - Í3(R5+R3) =0 Аналогично для второй и третьей схем.
Решение систем находим средствами Mathcad:  Получаем решения для трех систем уравнений: Í1=0.9167 A; Í́́ 2= - 0.6875 A; Í́́ 3= 0.2292A Í ́1= -0.625A; Í́́ ́ 2= 1.0938 A; Í́́ ́ 3= 0.4688 A Í ́́ ́1 = 0.3125 A; Í́́ ́ ́ 2 = 0.7031 A; Í́́ ́ ́ 3 = 1.0156 A Используя метод наложения, находим истинные тока схемы: I1= Í1+ Í́́ ́1 +Í́́ ́ ́1 = 0.9167+(- 0.625)+ (- 0.3125)= - 0.0208 A; I2= Í2+ Í́́ ́2+Í́́ ́ ́2 = - 0.6875 +1.0938 + (- 0.7031) = - 0.2969A; I3= Í3+ Í́́ ́3 +Í́́ ́ ́3= - 0.2292+(-0.4688) + 1.0156 = 0.3177 A Итак, токи равны: I1= - 0.0208 A; I2= -0.2969A; I3= 0.3177 A Баланс мощностей для такой схемы (без ветви с R6) Равенство P1 = P2 выполняется (где Р1 – мощность источников в ваттах, Р2 – мощность потребителей в ваттах) |
