анализ экономических показателей. 19-образ. Задача методом математического программирования
 Скачать 30.29 Kb.
|
|
1. Задача методом математического программирования Для изготовления любого из 2-х видов продукции (А1 – печенья «Земляничное» и А2 – печенья «Кофе») требуется 3 вида продуктов (мука, сахар, яйца), на изготовление партии печенья «Земляничное» требуется затратить продуктов каждого вида: муки 3 кг, сахара 2 кг, яиц – 10. На изготовление партии печенья «Кофе» требуется муки 4 кг, сахара 1 кг, яиц – 5. При реализации i-го вида продукции предприятие получает прибыль Pi: от реализации 1-й партии печенья «Земляничное» прибыль составляет P1=42 тыс. руб., печенья «Кофе» – P2=26 тыс. руб. Составить план выпуска продукции, при котором предприятие получит максимальную прибыль.
Решение. Построим экономико-математическую модель задачи вида:  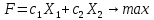 Пусть Х1 – объем производства изделия А1, Х2 – объем производства изделия А2. Поскольку объемы производства не могут быть отрицательным, получим:  .Ограничения по расходу каждого вида ресурсов будут иметь вид: - сырье 1 (мука):  Общие затраты сырья на производство «Земляничное» составят 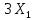 , на производство «Кофе» -  . Запасы: муки равен 600 кг, общие его затраты не должны превышать это значение.- сырье 2 (сахар): 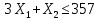 - сырье 3 (яйца):  Функция прибыли предприятия:  Поскольку необходимо максимизировать прибыль, то экономико-математическая модель задачи примет вид:  Решим прямую задачу линейного программирования В 1-м неравенстве смысла (≤) вводим базисную переменную x3. В 2-м неравенстве смысла (≤) вводим базисную переменную x4. В 3-м неравенстве смысла (≤) вводим базисную переменную x5. Подставим их в функцию: 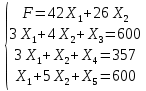 Основные данные задачи можно представить в виде таблицы:
В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент по модулю. Вычислим значения Di по строкам как частное от деления: bi / ai1 и из них выберем наименьшее: min (600 : 3 , 357 : 3 , 600 : 1 ) = 119 Следовательно, 2-ая строка является ведущей. Разрешающий элемент равен (3) и находится на пересечении ведущего столбца и ведущей строки. Основные данные задачи можно представить в виде таблицы:
Текущий опорный план не оптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент по модулю. Вычислим значения Di по строкам как частное от деления: и из них выберем наименьшее: min (243 : 3 , 119 : 1/3 , 481 : 42/3 ) = 81 Следовательно, 1-ая строка является ведущей. Разрешающий элемент равен (3) и находится на пересечении ведущего столбца и ведущей строки. Основные данные задачи можно представить в виде таблицы:
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи: X1 = 92, X2 = 81, X3 = 0, X4 = 0, X5 = 103 F(X) = 42*92 + 26*81 = 5970 тыс. руб. Таким образом, максимальная прибыль при заданных ограничениях ресурсов достигается при производстве 92 партий печенья «Земляничное» и 81 партии печенья «Кофе». Максимальная прибыль составляет 5970 тыс. руб. Задание 2. Решить задачу по экономическому анализу Используя разные методы экономического анализа (сравнение, графический, табличный и др.), проанализировать выполнение плана и определить задачи на будущий период. Данные по производству овощей открытого грунта, тонн представлены в таблице 1. Таблица 1. Анализ производства овощей открытого грунта, в тоннах
Задание. Произведите анализ выполнения плана производства овощей за первые три месяца. Для этого рассчитайте производные показатели по формулам: Абсолютное изменение ∆ = Yф - Y пл Коэффициент выполнения плана, выраженный в %: Кпл = Yф / Yпл Относительное изменение плана в % ∆% = Кпл% - 100 ∆% = (∆ / Yпл) * 100 Абсолютное изменение: Коэф. выполнения плана: Капуста ранняя 190-185=5 капуста ранняя 190/185=1,027*100=102,70 Капуста поздняя 275-266=9 капуста поздняя 275/266=1,033*100=103,38 Огурцы 136-157= - 21 огурцы 136/157=0,866*100=86,62 Томаты 195-210= - 15 томаты 195/210=0,928*100=92,86 Морковь 216-235= - 19 морковь 216/235=0,919*100=91,91 Лук 253-242= 11 Лук 253/242=1,045*100=104,55 Относительное изменение плана: Капуста ранняя= 102,70-100= 2,70 Капуста поздняя= 103,38-100= 3,38 Огурцы= 86,62-100= - 13,38 Томаты= 92,86-100= - 7,14 Морковь= 91,91-100= - 8,09 Лук= 104,55-100= 4,55 Таблица 2. Анализ выполнения плана производства овощей.
На основании данных таблицы, можно сделать вывод результата расчетов таблицы 2, план по производству овощей открытой почвы: капуста (ранняя), капуста (поздняя), лук – выполнен, план производства овощей: лук – на 4,55% (104,55%-100%) или 11,00 тонн. План по производству таких овощей: огурцы, томаты, морковь –не выполнен, производству овощей: огурцы – на 13,38% (86,62%-100%) или 21,00 тонн. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||