Задача на максимум, то двойственная на минимум. Получаем 15 y

• Название: Задача на максимум, то двойственная на минимум. Получаем 15 y
• Анкор: 123213
• Дата: 14.05.2022
• Размер: 31.53 Kb.
• Имя файла: №2.docx
• Тип: Задача; #529531

Найти максимальное значение целевой функции F(X) = 5x-4y при следующих условиях-ограничений: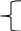


5x+7y≤15
7x+8y₂≤13
4x+3y≥10

1. 
   Данная задача в стандартной форме: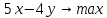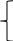
   

5x+7y≤15
7x+8y₂≤13
4x+3y≥10

x,y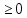
б) Для приведения в каноническую форму введем в 1м неравенстве базисную переменную x₃. Во 2м неравенстве базисную переменную x₄. В 3м неравенстве базисную переменную x₅ со знаком минус.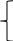


5x₁+7x₂+x₃ = 15
7x₁+8x₂+x₄ = 13
4x₁+3x₂-x₅ = 10

x,y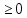
в) Двойственная задача. Количество переменных в двойственной задаче равно количеству неравенств в исходной. Матрица коэффициентов двойственной задачи является транспонированной к матрице коэффициентов исходной. Система ограничений двойственной задачи записывается в виде неравенств противоположного смысла неравенствам системы ограничений прямой задачи. Если исходная задача на максимум, то двойственная на минимум. Получаем:

15y₁+13y₂+10y₃ → min

5y₁+7y₂+4y₃≥5
7y₁+8y₂+3y₃≥-4
y₁ ≥ 0
y₂ ≥ 0
y₃ ≤ 0

Г) Для исходной системы строим начальную симплекс-таблицу. Искусственные переменные вводить нужно, получаем ограничения:

5x₁+7x₂+x₃ = 15
7x₁+8x₂+x₄ = 13
4x₁+3x₂-x₅ = 10

x,y

Выразим базисные переменные через остальные:
x₃ = -5x₁-7x₂+15
x₄ = -7x₁-8x₂+13
x₅ = 4x₁+3x₂-10
Подставим их в целевую функцию:
F(X) = 5x₁-4x₂

Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.

Базис	B	x1	x2	x3	x4	x5
x3	-25/3	-13/3	0	1	0	7/3
x4	-41/3	-11/3	0	0	1	8/3
x2	10/3	4/3	1	0	0	-1/3
F(x)	40/3	31/3	0	0	0	-4/3

Представим расчет каждого элемента в виде таблицы:

B	x1	x2	x3	x4	x5
15-(-10 • 7):-3	5-(-4 • 7):-3	7-(-3 • 7):-3	1-(0 • 7):-3	0-(0 • 7):-3	0-(1 • 7):-3
13-(-10 • 8):-3	7-(-4 • 8):-3	8-(-3 • 8):-3	0-(0 • 8):-3	1-(0 • 8):-3	0-(1 • 8):-3
-10 : -3	-4 : -3	-3 : -3	0 : -3	0 : -3	1 : -3

Получаем:

Базис	B	x1	x2	x3	x4	x5
x3	86/11	0	0	1	-13/11	-9/11
x1	41/11	1	0	0	-3/11	-8/11
x2	-18/11	0	1	0	4/11	7/11
F(x1)	-277/11	0	0	0	31/11	68/11

Представим расчет каждого элемента в виде таблицы:

B	x1	x2	x3	x4	x5
-81/3-(-132/3 • -41/3):-32/3	-41/3-(-32/3 • -41/3):-32/3	0-(0 • -41/3):-32/3	1-(0 • -41/3):-32/3	0-(1 • -41/3):-32/3	21/3-(22/3 • -41/3):-32/3
-132/3 : -32/3	-32/3 : -32/3	0 : -32/3	0 : -32/3	1 : -32/3	22/3 : -32/3
31/3-(-132/3 • 11/3):-32/3	11/3-(-32/3 • 11/3):-32/3	1-(0 • 11/3):-32/3	0-(0 • 11/3):-32/3	0-(1 • 11/3):-32/3	-1/3-(22/3 • 11/3):-32/3

Выразим базисные переменные через остальные:
x₃ = ¹³/₁₁x₄+⁹/₁₁x₅+7⁹/₁₁
x₁ = ³/₁₁x₄+⁸/₁₁x₅+3⁸/₁₁
x₂ = -⁴/₁₁x₄-⁷/₁₁x₅-1⁷/₁₁
Подставим их в целевую функцию:
F(X) = 5(³/₁₁x₄+⁸/₁₁x₅+3⁸/₁₁)-4(-⁴/₁₁x₄-⁷/₁₁x₅-1⁷/₁₁)

Г) Опорный план:

Базис	B	x1	x2	x3	x4	x5
x3	86/11	0	0	1	-13/11	-9/11
x1	41/11	1	0	0	-3/11	-8/11
x2	-18/11	0	1	0	4/11	7/11
F(x)	0	0	0	0	-31/11	-68/11

x3, x4, x5 – базисные переменные
x1, x2 - свободные