вариант 5. Задача Найти матрицу d ab 2 c решение 1 Найдем матрицу 2 c 2 Найдем матрицу

• Название: Задача Найти матрицу d ab 2 c решение 1 Найдем матрицу 2 c 2 Найдем матрицу
• Дата: 21.02.2023
• Размер: 207.08 Kb.
• Имя файла: вариант 5.docx
• Тип: Задача; #948156

Вариант 5

Задача 5. Найти матрицу D = AB-2C



Решение

1) Найдем матрицу 2C



2) Найдем матрицу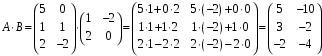



3) Найдем матрицу D = AB-2C



Ответ: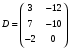
Задача 15. В задачах 11 – 20 дана невырожденная матрица A. Найти обратную матрицу A^-1 и пользуясь правилом умножения матриц, показать, что
A·A^-1 = Е, где E – единичная матрица.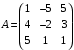



Решение



Основной определитель системы отличен от нуля, значит, обратная матрица существует.

Транспонируем исходную матрицу:

Находим алгебраические дополнения элементов матрицу :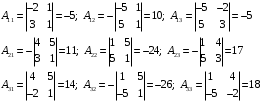



Получаем обратную матрицу: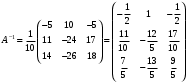

.

Проверим правильность решения:



Ответ: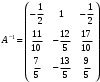
Задача 25. В задачах 21 – 30 решить системы линейных уравнений с тремя неизвестными.



Решение

Решим систему уравнений методом Крамера

Согласно методу Крамера неизвестные х_i находят по формуле: , где Δ – определитель матрицы, состоящий из коэффициентов при неизвестных СЛАУ, Δ_i– определитель матрицы, полученный из Δ заменой i-ого столбца на столбец свободных коэффициентов.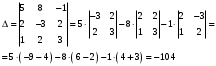



Δ ≠ 0, значит система имеет единственное решение.



Тогда

Ответ:
Задача 35. В задачах 31 –40 построить треугольник, вершины которого находятся в точках 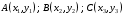. Найти:

1) уравнения сторон треугольника ABC;

2) координаты точки М пересечения медиан;

3) длину и уравнение высоты, опущенной из вершины A;

4) площадь треугольника.



Решение

1) Уравнение прямой, проходящей через две заданные точки:



Найдем уравнение стороны АВ: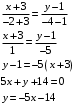



Найдем уравнение стороны ВC:



Найдем уравнение стороны АC:



2) Найдем середину отрезка ВС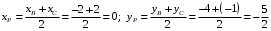



Получили координаты точки

Уравнение прямой, проходящей через две заданные точки: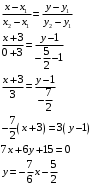



Найдем середину отрезка AС



Получили координаты точки

Уравнение прямой, проходящей через две заданные точки:



Найдем середину отрезка AB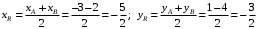



Получили координаты точки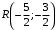

Уравнение прямой, проходящей через две заданные точки:



Найдем координаты точки М пересечения медиан, решив систему уравнений:



Получили координаты точки

3) Прямая, проходящая через точку N₀(x₀;y₀) и перпендикулярная прямой
Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: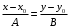

Таким образом, получаем: или



Найдем длину высоты как расстояние от точки до прямой



4) Воспользуемся формулой: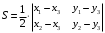



Тогда





Ответ: 1) ; ;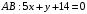

2)

3) 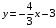; 4.6

4) 11.5 ед²
Задача 45. В задачах 41 – 50 даны координаты точек А(х₁, y₁, z₁), В(х₂, y₂, z₂), С(х₃, y₃, z₃),D(х₄, y₄, z₄). Найти:

1) найти длину ребра AB;

2) уравнение плоскости, проходящей через точки A, B и C;

3) длину высоты пирамиды, опущенной из вершины D;

4) площадь грани АВС;

5) объем пирамиды ABCD.



Решение

1) Найдем координаты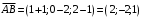

Найдем длину

2) Найдем уравнение плоскости АВС:

Уравнение плоскости, проходящей через три заданные точки:





3) Найдем расстояние от точки D до найденной плоскости



4) Найдем площадь грани АВС.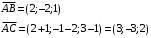



Находим векторное произведение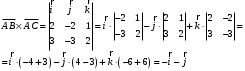



Тогда площадь грани:

(ед²)

5) Найдем объем пирамиды.



Находим смешанное произведение



Тогда объем пирамиды (ед³)

Ответ: 1) 3; 2) ; 3) 0.707 ед²; 4) 0.167 ед³.