САУ. Задача Найти реакцию апериодического звена на ступенчатое воздействие 1t
 Скачать 42.74 Kb. Скачать 42.74 Kb.
|
|
Блок №3 Задача 1. Найти реакцию апериодического звена на ступенчатое воздействие 1[t]; В динамике апериодическое звено описывается следующим дифференциальным уравнением: a1x(t) + a0x (t) = b0z(t) Разделим обе части уравнения на a0 и заменим T=a1/a0; k=b0/a0 Получаем: Tx(t)+x(t)=kz(t) Так как: Следовательно: Множитель 1(t) обеспечивает равенство нулю при t ≤ 0 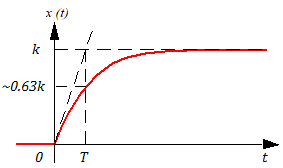 Реакция апериодического звена на единичное ступенчатое воздействие на рисунке Постоянная времени Т характеризует инерционность переходных процессов в звене. Чем больше Т, тем медленнее идет переходной процесс. Задача 5 Передаточная функция имеет вид: W(s)=Ks/(Ts+1) Данная передаточная функция является реальным дифференцирующим звеном Найдем дифференциальное уравнение САР Фактически такое звено можно получить, перемножив передаточные функции идеального дифференцирующего и инерционного звеньев, соединенных последовательно: 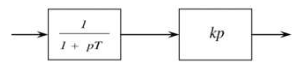 В этом случае дифференциальное уравнение будет иметь вид: Или: W(s)=Ks/(Ts+1)=  Следовательно:  ; ;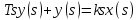 ; ;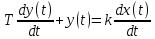 Блок №3 Задача 1. Перечислить первичные показатели качества К основным показателям качества относятся: - быстродействие, tпп - время переходного процесса, по истечении которого отклонение управляемой величины y(t) относительно заданного значения yзад по абсолютному значению становится (и остается в дальнейшем) меньше определенной заданной величины уст - перерегулирование s; Перерегулирование характеризует колебательные свойства процессов - колебательность М; - статическая и динамическая точность; - добротность системы. Задача 7. Понятие запаса устойчивости. В условиях эксплуатации параметры системы по тем или иным причинам могут меняться в определенных пределах (старение, температурные колебания и т.п.). Эти колебания параметров могут привести к потере устойчивости системы, если она работает вблизи границы устойчивости. Поэтому стремятся спроектировать систему так, чтобы она работала вдали от границы устойчивости. Степень этого удаления называют запасом устойчивости. Согласно критерию Найквиста, чем дальше АФЧХ от критической точки (-1, j0), тем больше запас устойчивости. Различают запасы устойчивости по модулю и по фазе. Запас устойчивости по модулю характеризует удаление годографа АФЧХ разомкнутой системы от критической точки в направлении вещественной оси и определяется расстоянием h от критической точки до точки пересечения годографом оси абсцисс. Запас устойчивости по фазе характеризует удаление годографа от критической точки по дуге окружности единичного радиуса и определяется углом между отрицательным направлением вещественной полуоси и лучом, проведенным из начала координат в точку пересечения годографа с единичной окружностью. Обычно при создании системы задаются требуемыми запасами устойчивости h и φ, за пределы которых она выходить не должна. Эти пределы выставляются в виде сектора, вычерчиваемого вокруг критической точки, в который АФЧХ разомкнутой системы входить не должна. |
