Передаточная функция апериодического звена. Контрольная работа. Задание 1 Задана передаточная функция апериодического звена Определить и построить афх, фчх и переходную характеристику h(t). Исходные данные Решение
 Скачать 52.58 Kb. Скачать 52.58 Kb.
|
|
Задание 1 Задана передаточная функция апериодического звена  Определить и построить АФХ, ФЧХ и переходную характеристику h(t). Исходные данные:   Решение: Переходная временная характеристика h(t) - реакция выхода системы на единичное ступенчатое воздействие 1(t) при нулевых начальных условиях [1]. Для нахождения временной характеристики звена определим его реакцию на единичное ступенчатое воздействие. Изображение переходной функции определяется как [2]   Характеристическое уравнение 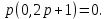 Корни уравнения  Выполняя обратное преобразование изображения переходной характеристики h(p) получаем 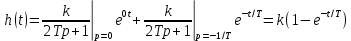 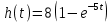 Переходная характеристика звена приведены на рис. 1.  Рисунок 1 - Переходная характеристика апериодического звена Найдем комплексную передаточную функцию (КПФ). Для этого заменим p на jω [2].  Зависимость модуля КПФ от частоты называется амплитудно-частотная характеристика (АЧХ) системы [2]  Амплитудно-частотная характеристика звена определяется как: 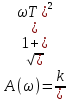 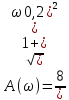 Для построения АЧХ найдем характерные точки: При 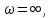  . .При 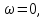  При 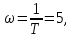  По рассчитанным значениям построим график АЧХ  Рисунок 2 - График АЧХ апериодического звена Зависимость аргумента КПФ представляет собой фазо-частотную характеристику (ФЧХ) системы [2] 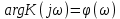 . .Вещественная 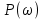 и и 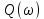 мнимая частотные характеристики звена определяются как мнимая частотные характеристики звена определяются как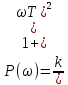  Фазо-частотная характеристика определяется как  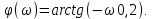 Для построения ФЧХ найдем характерные точки: При 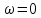 , , 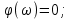 При 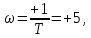 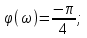 При 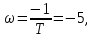 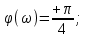 При 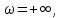  При 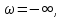  По рассчитанным значениям построим график ФЧХ 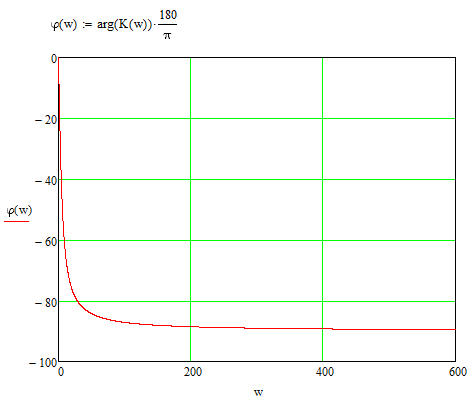 Рисунок 3 - График ФЧХ апериодического звена Задание 2 Задана передаточная функция разомкнутой системы управления  Оценить устойчивость системы по критерию Гурвица. Исходные данные: 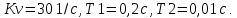  Решение: Найдем передаточную функцию замкнутой системы  Характеристический полином замкнутой системы 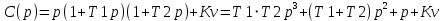 Обозначим   Критерий Гурвица: для того, чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы все диагональные миноры имели знаки, одинаковые со знаком первого коэффициента характеристического уравнения C0, то есть при C0 > 0 были положительны. Эти миноры называются определителями Гурвица [3]. Составим определитель Гурвица по следующему правилу: по главной диагонали определителя слева направо в порядке возрастания индексов выписывают все коэффициенты характеристического уравнения от  до до  . Столбцы вверх от главной диагонали дополняют коэффициентами характеристического уравнения с последовательно возрастающими индексами, а столбцы вниз – с последовательно убывающими индексами. На место коэффициентов с индексами больше . Столбцы вверх от главной диагонали дополняют коэффициентами характеристического уравнения с последовательно возрастающими индексами, а столбцы вниз – с последовательно убывающими индексами. На место коэффициентов с индексами больше  и меньше и меньше  проставляют нули [3]. проставляют нули [3]. Вычислим диагональные миноры при 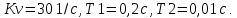 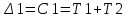 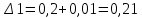 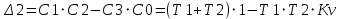 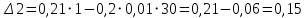  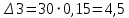 Так как С0 > 0, и все диагональные миноры больше нуля, то рассматриваемая система устойчива. Задание 3 На САУ с разомкнутой передаточной функцией  действует управляющий сигнал  . Определить ошибку в установившемся режиме. . Определить ошибку в установившемся режиме.Исходные данные:  Решение: Для установившейся ошибки воспроизведения медленно меняющихся управляющих воздействий было получено выражение, имеющее для непрерывных систем следующую форму[2] 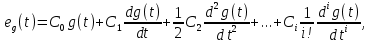 где 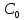 , , 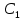 , , 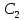 , …, , …,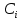 - коэффициенты ошибок, определяемые по выражению - коэффициенты ошибок, определяемые по выражению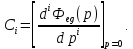 Так  где где 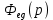 - передаточная функция замкнутой системы по ошибке от воздействия g(t) [2]. - передаточная функция замкнутой системы по ошибке от воздействия g(t) [2]. Используя выражение для установившейся ошибки через коэффициенты ошибок, найдем значение коэффициентов ошибок при отработке непрерывной системой линейного воздействия  . .Порядок астатизма системы υ = 1. Передаточная функция замкнутой системы по ошибке 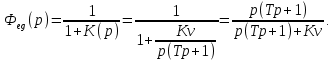 Установившаяся ошибка при отработке линейного воздействия 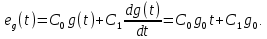 Определим коэффициенты ошибок 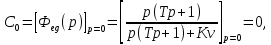 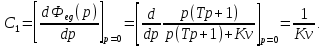 Установившееся значение ошибки  БИБЛИОГРАФИЧЕСКИЙ СПИСОК Гаркушенко, В.И. Теория автоматического управления: учебное пособие / В.И. Гаркушенко, Г.Л. Дегтярев. - Казань: Гос.тех.ун-та, 2010. – 274 с. Козлова, Л.П. Теория автоматического управления. ч. 1: учебно-методический комплекс / Л.П.Козлова, О.И.Золотов. - СПб.: Изд-во СЗТУ, 2009. – 252 с. Усынин, Ю.С. Теория автоматического управления: учебное пособие для вузов / Ю.С. Усынин. – Челябинск: Издательский центр ЮУрГУ, 2010. – 176 с. |
