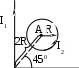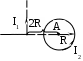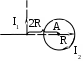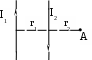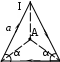РГР- электричество и магнетизм. Задача напряженность

• Название: Задача напряженность
• Дата: 01.05.2023
• Размер: 0.55 Mb.
• Имя файла: РГР- электричество и магнетизм.doc
• Тип: Решение; #1100714
• страница: 3 из 3

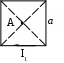
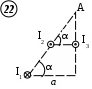
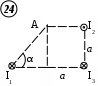
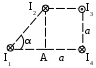
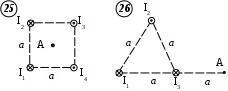
Пример решения 26-го варианта
В поле, созданном бесконечной равномерно заряженной плоскостью с плотностью заряда σ = 10^-6 Кл/м² и точечным зарядом q = 10^-7 Кл, на расстоянии b = 0,1 м от плоскости в точке В находится точечный заряд Q = 10^-6 Кл. Расстояние между зарядами 2b. Найти работу перемещения заряда Q в точку С, лежащую на расстоянии b от плоскости и на расстоянии b от заряда q на перпендикуляре, восстановленном из этого заряда к плоскости.


Дано:

σ = 10^-6 Кл/м²

q = 10^-7 Кл

Q = 10^-6 Кл

b = 0,1 м

с =
А – ?
Решение: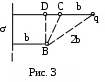

Работу перемещения найдем из формулы А = q(φ_В – φ_С). Разность потенциалов (φ_В – φ_С) равна алгебраической сумме разностей потенциалов плоскости Δφ_σ и заряда q Δφ_q. Δφ_σ, созданную плоскостью, найдем по формуле , где

Е = , . (потенциалы поля, созданного плоскостью в точках D и В, равны). Теперь , где . DC = c – b = b( – 1).

.

Потенциал точечного заряда вычисляется по формуле .

Тогда φ_В = , φ_С = и

Δφ_q = ;

Δφ_q = -9 ∙ 10⁹ ∙ 10^-7/(2 ∙ 0,1) = -4,5 ∙ 10³ В.

Окончательно работа есть А = 10^-6 ∙ (4,14 ∙ 10³ - 4,5 ∙ 10³) = -0,36 ∙ 10³ Дж.

Ответ: А = -0,36 ∙ 10³ Дж.

Проверим размерность: [A] = [Кл] ∙ [B] = [Дж].
ЗАДАЧА 3. ОПРЕДЕЛЕНИЕ ИНДУКЦИИ

МАГНИТНОГО ПОЛЯ ТОКОВ
Найти магнитную индукцию в точке А. Номера вариантов проставлены в левом верхнем углу приведенных ниже рисунков.

I1 = I2 = 1 A r1 = r2 = 2 см		I1 = I2 = 0,5 A r1 = r2 = 2 см	I1 = I2 = 1 A r1 = r2 = 5 см
r1 = r2 = 2 см R1 = R2 = 2 см I1 = I2 = 1 A	r1 = r2 = 2 см R1 = R2 = 3 см I1 = I2 = 1 A		r1 = r2 = 1 см R1 = R2 = 2 см I1 = I2 = 1 A
R = 10 см I1 = I2 = 0,5 A	R = 1 см I1 = I2 = 1 A		R = 1 см I1 = I2 = 1 A
r1 = r2 = 2 см I1 = I2 = 1 A	1 = 4a = 20 см I1 = 0,5 А		а = 5 см I1 = I2 = I3 = 1 A
а = 2 см α = 600 I1 = I2 = I3 = 1 A	а = 2 см α = 600 I = 1 A		а = 2 см α = 600 I1 = I2 = I3 = I4 = 1 A
R = 2 см, r1 = r2 = 5 см I1 = I2 = I3 = 1 A	r1 = r2 = r3/2 = 2 см I1 = I2 = I3 = 0,5 A		a = 3 см I1 = I2 = I3 = 1 A
r2
α = 450, r1 = r2 = 5 см I1 = I2 = I3 = 1 A	r1 = 5 см r2 = 4 см I1 = I2 = 0,5 A		а = 5 см I1 = I2 = 1 A
а = 5 см, α = 450 I1 = I2 = I3 = 1 A	а = 5 см, α = 450 I1 = I2 = I3 = I4 = 1 A		а = 2 см, α = 450 I1 = I3 = 2I2 = 0,2 A
а = 5 см, I1 = I4 = 0,5 А I2 = I3 = 1 A	а = 3 см, I2 = 4 А I1= I3 = 1 A

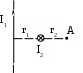
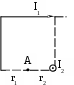
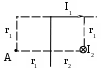
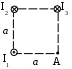
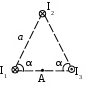
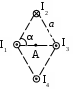
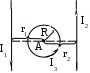
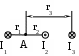
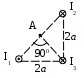
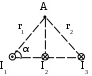
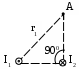
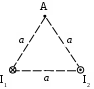
Пример решения задачи 26-го варианта


Дано:

I₁ = I₃ = 1 A

I₂ = 4 A

а = 3 см
В – ?



Решение: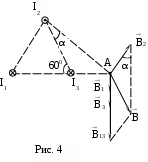

Покажем направления векторов индукции магнитных полей. Магнитные поля В₁ и В₃, направленные одинаково, найти просто по формуле для бесконечно длинного прямолинейного проводника:

,

.

Магнитные поля подчиняются принципу суперпозиции. Поэтому равнодействующая полей В₁, В₂

.

Для нахождения В₂ надо знать расстояние до точки А от тока I₂. Его, например, найдем по теореме косинусов . Теперь . Построив равнодействующую из векторов В₂ и В₁₃, найдем ее длину. Вновь по теореме косинусов
,

где α = 30⁰, как нетрудно найти.

С учетом того, что I₂ = 4I₁, получаем

;

;

.
Ответ: В = 16,4 мкТл.

Проверка размерности достаточно очевидна.

ЗАДАЧА 4. СИЛА ЛОРЕНЦА, СИЛА АМПЕРА,

ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ ФАРАДЕЯ
Примечание: в вариантах, в которых рассматривается α-частица, считать ее массу равной четырем массам протона. Заряд α-частицы равен по модулю двум зарядам электрона.

1. 
   В однородном магнитном поле с индукцией В = 100 мкТл по винтовой линии движется электрон. Определить его скорость вращения, если шаг h винтовой линии равен 20 см, а радиус вращения R = 5 см.
   

Ответ: 1,04 ∙ 10⁶ м/с.

2. 
   В однородном магнитном поле с индукцией В = 20 мкТл по винтовой линии движется электрон. Электрон влетел в поле под углом 30⁰ к силовым линиям, имея импульс р = 10^-24 кг∙м/с. Найти радиус вращения электрона. Ответ: 0,16 м.
   
3. 
   Электрон влетает в однородное магнитное поле под углом 45⁰ к силовым линиям, имея энергию W = 5,5 ∙ 10^-19 Дж. Магнитная индукция В = 10 мкТл. Найти радиус вращения электрона. Ответ: 0,44 м.
   
4. 
   Электрон влетает под некоторым углом в однородное магнитное поле с индукцией В = 30 мкТл, имея импульс р = 10^-25 кг∙м/с. Радиус вращения R = 1,04 см. Определить угол, под которым электрон влетел в поле.
   

Ответ: α = 30⁰.

5. 
   α-частица и протон вращаются по окружности с одинаковой скоростью в одном и том же однородном магнитном поле. Во сколько раз различаются их радиусы вращения? Ответ: в 2 раза.
   
6. 
   α-частица и протон вращаются по окружности с одинаковой скоростью в одном и том же однородном магнитном поле. Во сколько раз различаются их периоды вращения? Ответ: в 2 раза.
   
7. 
   Протон влетает перпендикулярно однородному магнитному полю. Во сколько раз и как изменится его радиус вращения, если поле увеличить в 2 раза, а протон влетит ортогонально этому полю с учетверенной энергией? Ответ: не изменится.
   
8. 
   Протон влетает перпендикулярно однородному магнитному полю. Во сколько раз и как изменится его радиус вращения, если поле увеличить в 2 раза, а протон влетит ортогонально этому полю с учетверенной энергией? Как изменится его период вращения? Ответ: не изменится.
   
9. 
   Протон прошел ускоряющую разность потенциалов U = 5 ∙ 10⁴ В и влетел ортогонально силовым линиям в однородное магнитное поле. Магнитная индукция В = 0,1 Тл. Найти радиус вращения протона.
   

Ответ: 0,14 м.

10. 
    Протон прошел ускоряющую разность потенциалов и влетел в однородное магнитное поле с индукцией В = 0,1 Тл под углом 60⁰ к силовым линиям. Шаг винтовой линии h = 0,454 м. Найти ускоряющую разность потенциалов. Ответ: 10⁴ В.
    
11. 
    Электрон прошел ускоряющую разность потенциалов U = 10⁴ В и влетел в однородное магнитное поле под углом 30⁰ к силовым линиям. Радиус вращения 1 см. Найти магнитную индукцию. Ответ: 16,9 мТл.
    
12. 
    α-частица прошла ускоряющую разность потенциалов U = 10⁴ В и влетела в однородное магнитное поле под углом 60⁰ к силовым линиям. Магнитная индукция 1 Тл. Найти шаг винтовой линии. Ответ: 6,42 см.
    
13. 
    Под влиянием однородного магнитного поля направленного вертикально, параллельно поверхности земли с ускорением а = 0,2 м/с² движется алюминиевый проводник сечением S = 1 мм². Проводник движется по направляющим без трения. По проводнику течет ток I = 5 А и его направление перпендикулярно полю. Найти индукцию поля В.
    

Ответ: 0,108 мТл.

14. 
    Медный прямолинейный проводник с током I сечением S = 0,5 мм² движется параллельно поверхности земли в однородном магнитном поле с индукцией В = 2 мТл перпендикулярно силовым линиям с ускорением а = 0,5 м/с². Найти ток, текущий в проводнике, если сам проводник перпендикулярен полю и движется по направляющим без трения. Индукционный ток не учитывать. Ответ: 1,12 А.
    
15. 
    Прямой проводник длиной l = 10 см, по которому течет ток силой I = 5 А, находится в однородном магнитном поле с индукцией В = 0,01 Тл. На провод действует сила Ампера F = 2,5 мН. Найти угол между направлениями вектора и тока. Ответ: 30⁰.
    
16. 
    Прямой алюминиевый провод некоторой длины, по которому протекает ток I, расположен в горизонтальном однородном магнитном поле перпендикулярно его силовым линиям. Провод находится во взвешенном состоянии. Индукция поля В = 0,1 Тл, сечение провода S = 2 мм². Найти ток в проводе. Ответ: 0,53 А.
    
17. 
    Прямой медный провод, по которому течет ток I = 5 А, расположен в горизонтальном однородном магнитном поле перпендикулярно его силовым линиям. Провод находится во взвешенном состоянии. Сечение провода S = 3 мм². Найти индукцию поля. Ответ: 53 мТл.
    
18. 
    Прямой никелевый провод, по которому течет ток I = 2 А, расположен в горизонтальном однородном магнитном поле перпендикулярно его силовым линиям. Провод находится во взвешенном состоянии. Индукция поля В = 1 Тл. Найти площадь поперечного сечения провода.
    

Ответ: 23 мм².

19. 
    Прямой провод некоторой длины, по которому течет ток I = 1 А, расположен в горизонтальном однородном магнитном поле перпендикулярно его силовым линиям. Провод находится во взвешенном состоянии. Индукция поля В = 0,1 Тл, сечение провода S = 3,78 мм². Из какого металла сделан провод? Ответ: алюминий.
    
20. 
    Параллельно поверхности земли расположен бесконечно длинный проводник, по которому течет некоторый ток I₁. Над этим проводником на расстоянии r = 1 см от него расположен отрезок алюминиевого проводника сечением S = 1 мм², находящийся в равновесии. Проводники параллельны друг другу. Найти ток I₁. Ответ: 66 А.
    
21. 
    Проводник длиной l = 20 см и сопротивлением R = 2 Ом согнут в виде квадрата, и концы его замкнуты. Квадрат помещен в однородное магнитное поле с индукцией 1 Тл так, что плоскость его перпендикулярна линиям индукции. Какой ток протечет по проводнику, если квадрат, потянув за противоположные вершины, за время t = 1 с вытянуть в линию? Ответ: 1,25 мА.
    
22. 
    Проводящее кольцо сопротивлением R = 4 Ом расположено в однородном магнитном поле с индукцией В = 1 Тл перпендикулярно силовым линиям. Взявшись за диаметрально противоположные точки кольца, его за 1 с вытянули в линию. При этом по кольцу протек ток I = 0,314 мА. Найти радиус кольца. Ответ: 2 см.
    
23. 
    Имеется проводящее кольцо сопротивлением R = 5 Ом с площадью S = 10 см². В некоторый момент в пространстве возникает магнитное поле, которое изменяется со временем по закону В = At, где А = 50 Тл/с. При этом линии индукции перпендикулярны плоскости кольца. Какой ток будет протекать по кольцу? Ответ: 10 мА.
    
24. 
    Имеется проводящее кольцо сопротивлением R = 4 Ом. В некоторый момент в пространстве возникает магнитное поле, которое начинает изменяться со временем по закону В = At, где А = 40 Тл/с. Линии индукции перпендикулярны плоскости кольца. При этом в кольце течет ток I = 50 мА. Определить площадь кольца. Ответ: 5 ∙ 10^-3 м².
    
25. 
    В однородном магнитном поле с индукцией В = 0,5 Тл равномерно с частотой ν = 10 с^-1 вращается рамка площадью S = 5 ∙ 10^-3 м². Ось вращения перпендикулярна силовым линиям. Найти максимальную ЭДС, возникающую в рамке. Ответ: 15,7 мВ.
    
26. 
    В пространстве параллельно поверхности земли расположен бесконечно длинный прямолинейный проводник, по которому течет ток I₁ = 10 А. Над этим проводником на расстоянии r = 1 см от него расположен отрезок никелевого проводника сечением S = 0,1 мм², находящийся в равновесии. Проводники параллельны друг другу. Найти ток I₂ в никелевом проводнике. Ответ: 43,1 А.
    

Пример решения задачи 26-го варианта


Дано:

I₁ = 10 А

r = 1 см = 10^-2 м

S = 0,1 мм² = 10^-7 м²

ρ = 8,8 ∙ 10³ кг/м³
I₂ – ?



Решение:

Сделаем рисунок. Так как никелевый проводник


находится в равновесии, это означает, что сила тяжести Р = mg уравновешена силой Ампера F, то есть I₂lB = mg. По закону Био-Савара-Лапласа найдем индукцию В, создаваемую током , а массу m отрезка длиной l распишем так: m = ρSl. Теперь или . Вычислим значение I₂ (плотность ρ берем из таблицы [1]):

.

Ответ: I₂ = 43,1 А.

Проверка размерности:
.


БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. 
   Чертов А. Г. Задачник по физике / А. Г. Чертов, А. А. Воробьев. – М.: Высш. шк., 1988. – 527 с.
   
2. 
   Волькенштейн В. С. Сборник задач по общему курсу физики / В. С. Волькенштейн. – СПб.: Книжный мир, 2003. – 327 с.
   
3. 
   Детлаф А. А. Курс физики: уч. пособ. для втузов / А. А. Детлаф, Б. М. Яворский. – М.: Высш. шк., 2002. – 718 с.
   
4. 
   Трофимова Т. И. Курс физики: уч. пособ. для вузов / Т. И. Трофимова. – М.: Высш. шк., 2000. – 542 с.