ЛР 4. Задача объезда. Задача объезда
 Скачать 1.21 Mb. Скачать 1.21 Mb.
|
Лабораторная работа 4Задача объездаЦель занятия: изучить способы постановки задач линейного программирования при организации деятельности центра МТО. Задача нахождения минимального пути объезда боевых участков. Рукавные линии, которые уже отработали на пожаре и замерзли (лабораторная работа 2 ч. 1), следует увозить на склад ПТЦ, для чего целесообразно разработать модель объезда боевых участков. Так как рукавная база, на которой осуществляется мойка, сушка и ремонт пожарных рукавов, как правило, находится в производственно-техническом центре, рукавные линии, которые уже отработали на пожаре и замерзли, следует увозить на склад ПТЦ, модель объезда боевых участков может быть записана в виде целевой функции 3. В ПТЦ по субъекту федерации для обслуживания гарнизона пожарной охраны имеется один автомобиль-полуприцеп, позволяющий перевозить замерзшие пожарные рукава на размораживание, мойку и сушку в ПТЦ. Пример: рассмотрим 3 пожара, на каждом из которых по несколько боевых участков, допустим их общее количество равно 3, 2 и 3 соответственно. Получается нам необходимо доставить пожарные рукава к месту их обслуживания. Рукава собраны в 8 линий, расположенных на разных расстояниях друг от друга. К каждой линии для погрузки рукавов автомобиль может подъехать только один раз. Требуется найти кратчайший замкнутый маршрут для сокращения общего пути объезда всех пожаров. В данном случае математическая модель объезда пунктов погрузки пожарных рукавов представляет собой частный случай транспортной задачи. Необходимо построить целевую функцию, где rij – расстояние между боевыми участками, при этом зададим условие, что в общем случае rij ≠ rji (расстояние между боевыми участками в прямом и обратном направлении не совпадают). 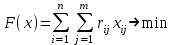 (3) (3)Условие: полуприцеп может объехать каждый боевой участок только один раз. Тогда условие однократного выезда из боевого участка: 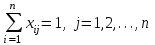 . (4) . (4)Условие однократного въезда на боевой участок для сбора рукавов: 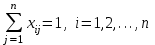 . (5) . (5)Зададим условие замкнутости маршрута движения, где ki и kj некоторые значения i, j = 1, 2, …, n, i ≠ j. ki – kj + nxij ≤ n-1, i, j = 1, 2, …, n, i ≠ j (6) xij = 0 или 1, i, j = 1, 2, …, n, i ≠ j (7) где xij – булевая переменная, принимает значение 1 если полуприцеп движется из i-го боевого участка к j-му и 0 в противном случае. В результате имеется 9 пунктов вывоза пожарных рукавов. Полуприцеп должен выехать из ПТЦ, посетить все боевые участки и вернуться обратно. Для сокращения времени следования полуприцепа найдем кратчайший маршрут, записав расстояние между боевыми участками в виде матрицы чисел (табл. 7). Таблица 7 – Матрица расстояний между боевыми участками
Чтобы полуприцеп двигался от одного боевого участка к другому с учетом минимальных расстояний между ними, в главную диагональ матрицы (расстояние от одного боевого участка в этот же участок) записываем расстояние намного большее по сравнению с другими. Например, 10000 км. Данный прием используется в так называемом методе «ветвей и границ» для исключения из маршрута движения нулевые по расстоянию переходы. Реализация: на рабочем листе необходимо разместить исходные данные (рис. 15) и матрицу переходов (рис. 36). На рис. 15 диапазон ячеек B3:K13 содержит исходную матрицу расстояний между боевыми участками, где расстояния равные 10000 означают что расстояние от боевого участка до себя не должно давать кратчайший маршрут движения полуприцепа. Данный прием подразумевает использование классического метода ветвей и границ, когда нулевые расстояния меняются на бесконечные [5]. 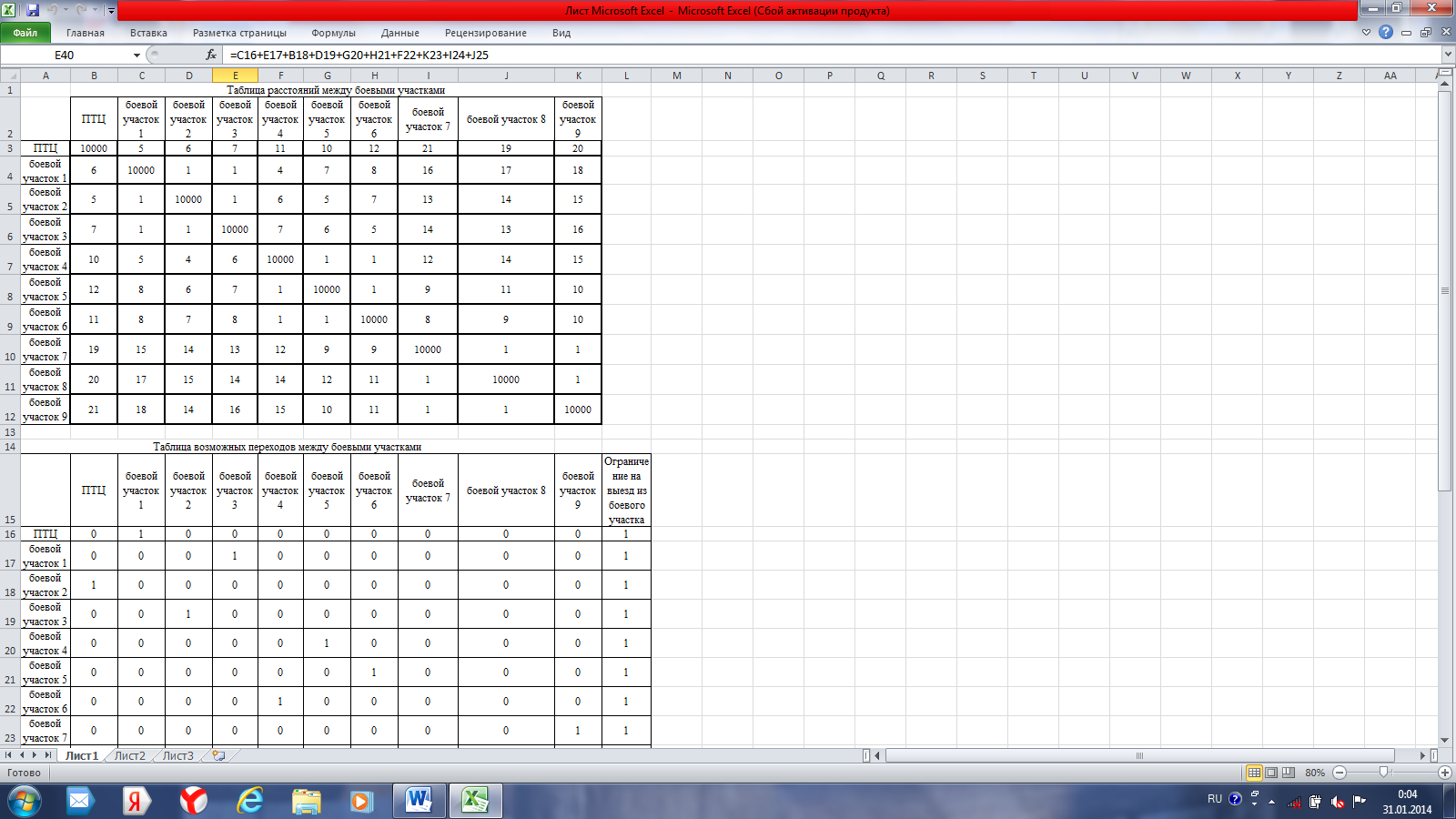 Рисунок 36 – Исходная матрица расстояний 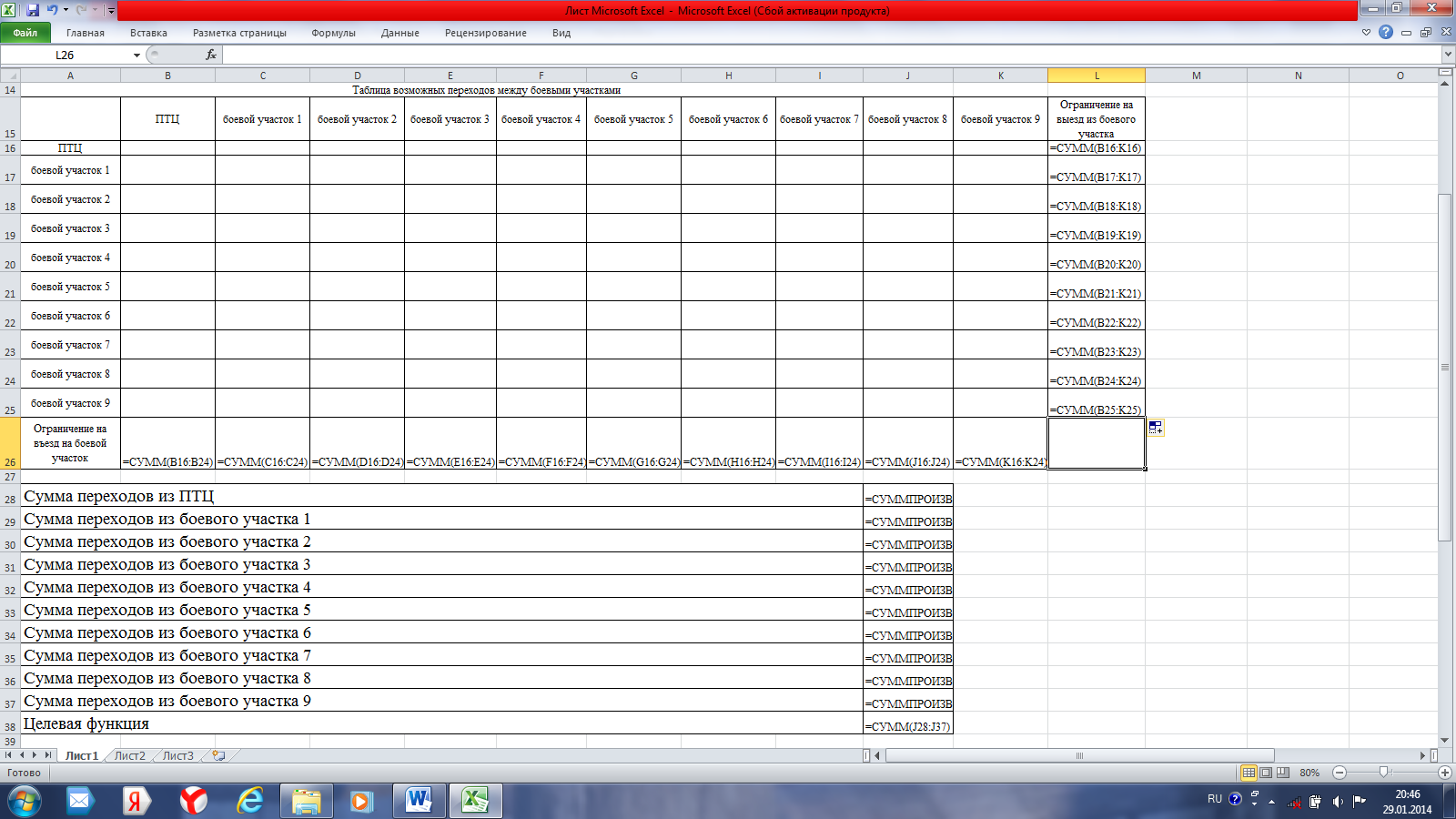 Рисунок 37 – Матрица переходов между боевыми участками Матрица возможных переходов от одного боевого участка к другому представлена рис. 36, диапазон ячеек B16:K25. Формулы для подсчета количества въездов и выездов из боевых участков занесены в ячейки В26:К26 и L16:L25. Данные формулы представляют из себя сумму столбцам и сумму по строкам матрицы переходов. Расчет целевой функции показан на рис. 37. 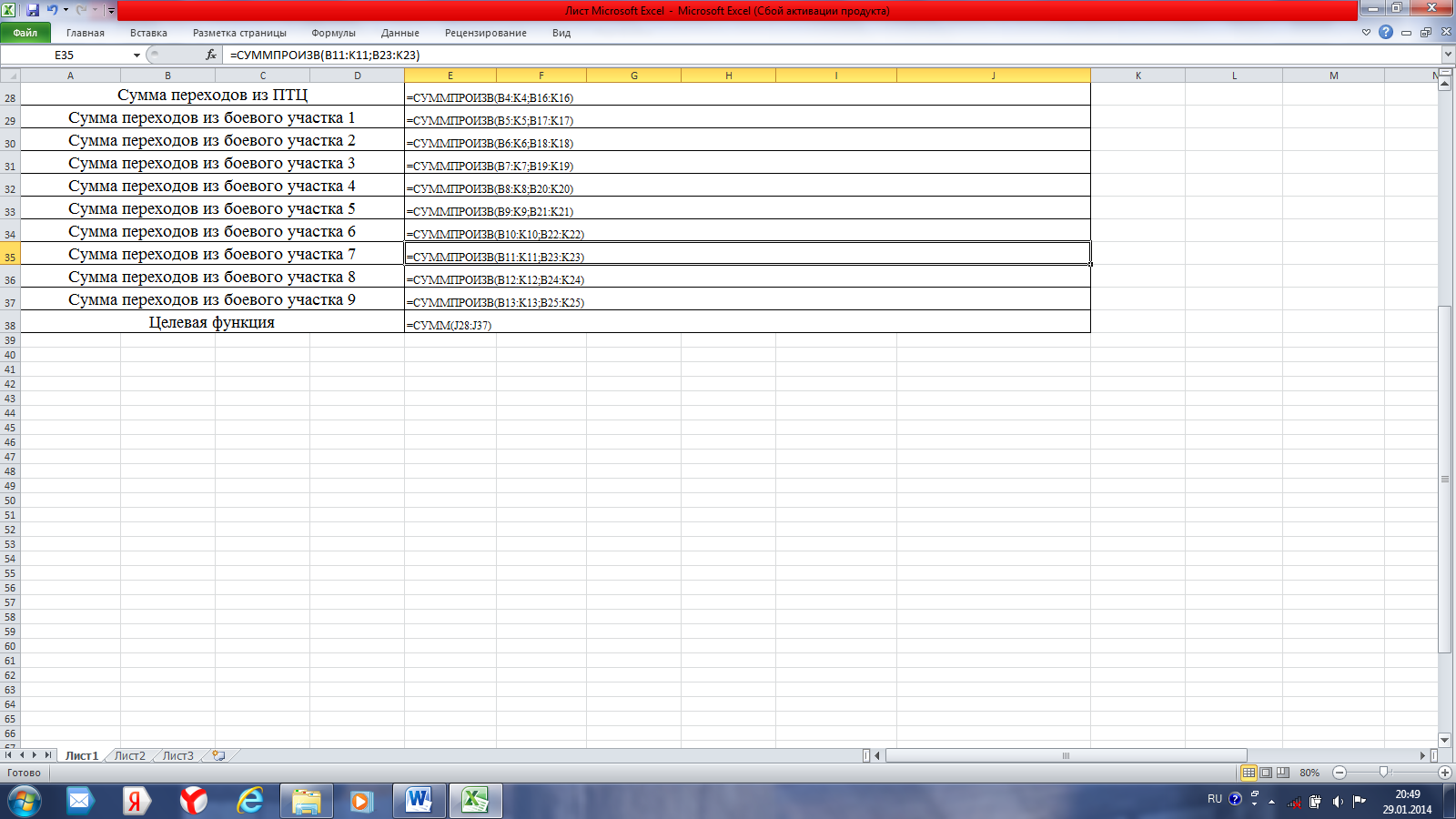 Рисунок 38 – Расчет целевой функции Строки Е28:Е37 содержат данные суммы произведений построчно исходной матрицы расстояний и матрицы переходов. Целевая функция расположена в ячейке Е38 и представляет сумму значений ячеек Е28:Е37. Далее формируется таблица ограничений (табл. 8). Таблица 8 – Ограничения на объезд боевых участков
Общий вид формы поиска решения представлен на рис. 39. 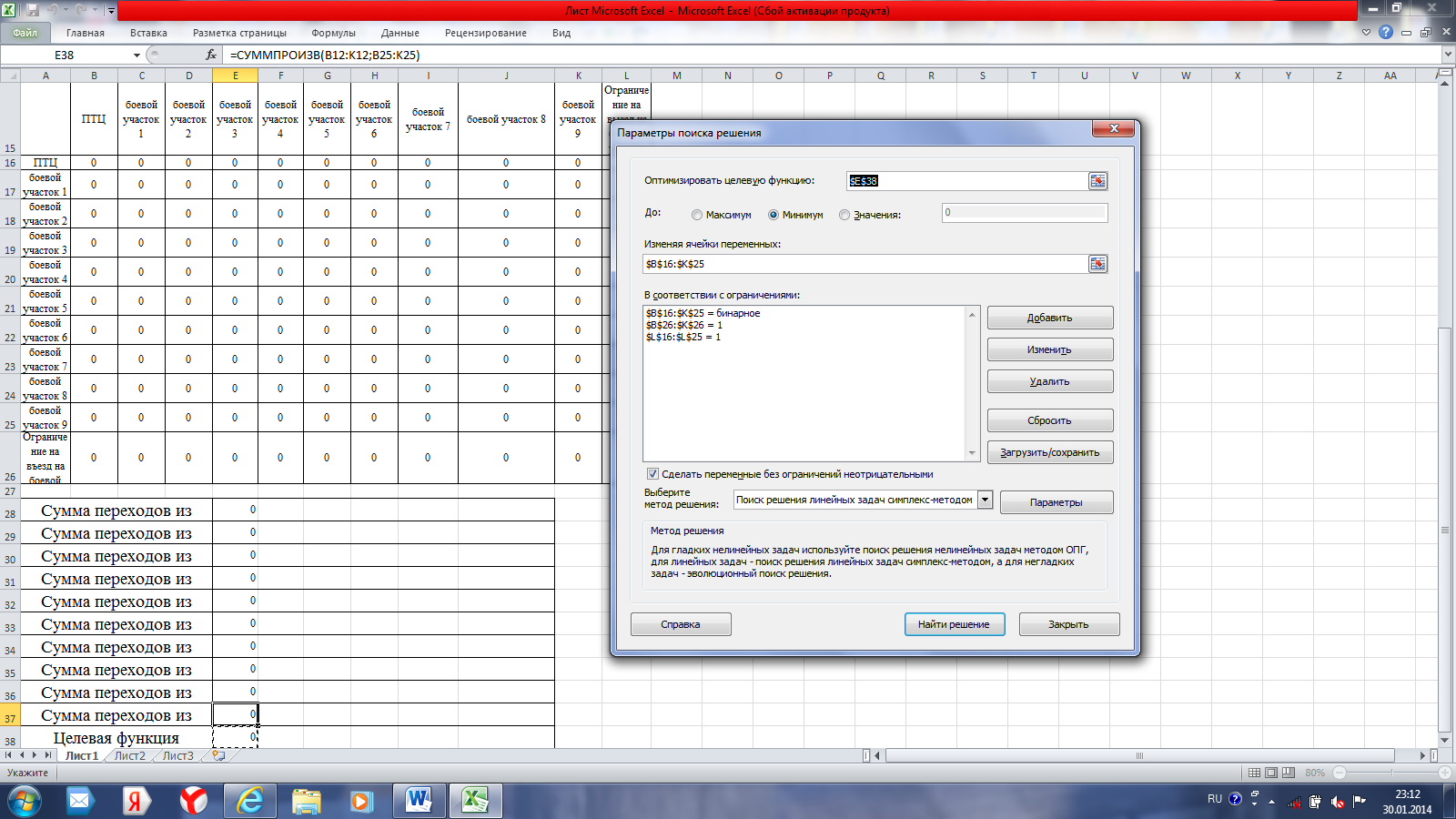 Рисунок 39 – Вид формы настройки параметров поиска решения в задаче 2 Итоговый план объезда боевых участков представлен на рис. 40. 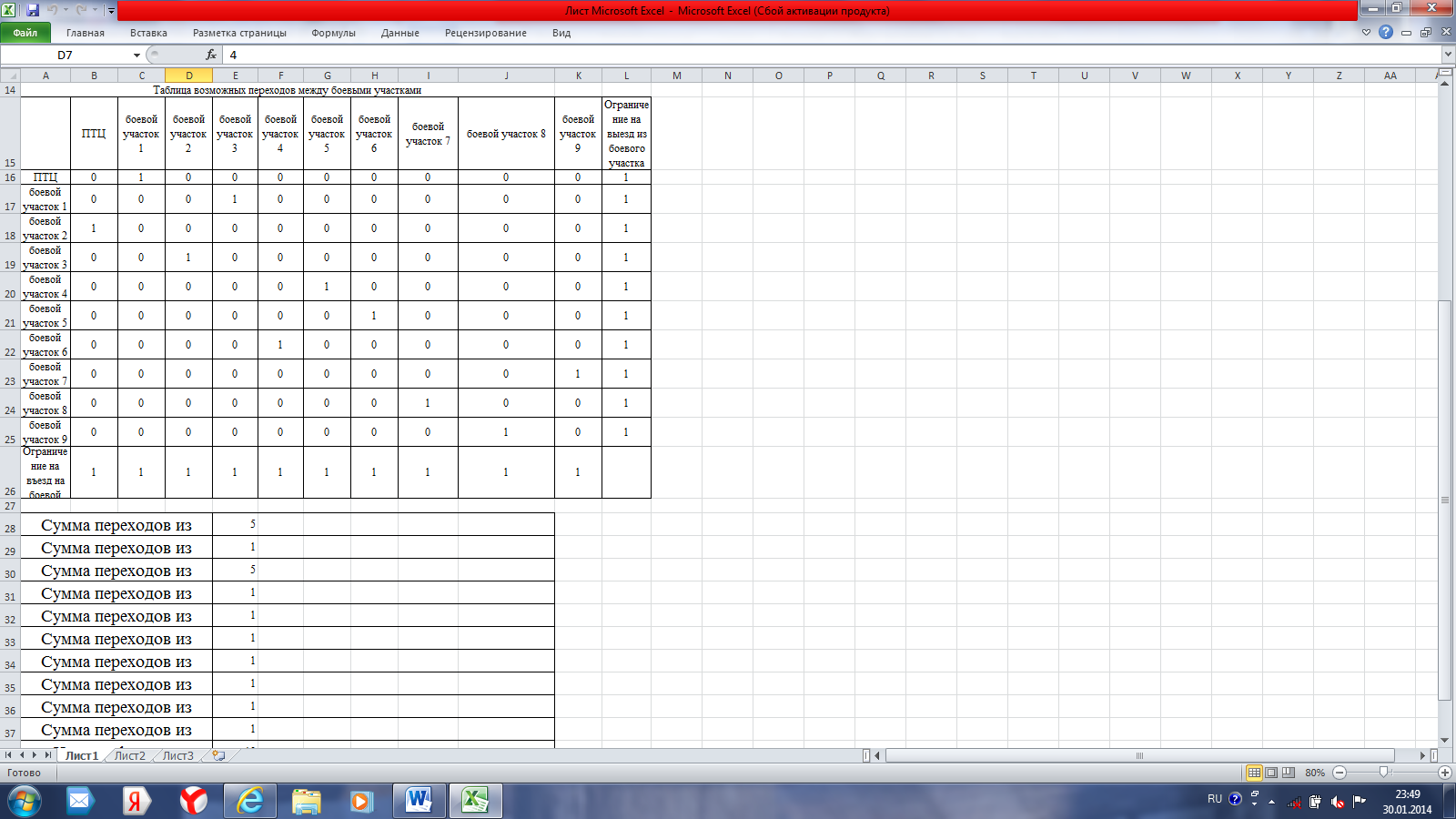 Рисунок 40 – План объезда боевых участков Так как в процессе поиска кратчайшего пути получилось четыре маршрута, задается дополнительное ограничение. Для этого в ячейке Е40 необходимо рассчитать количество переходов просуммировав ячейки =СУММ(С16;Е17;В18;D19;G20;H21;F22;K23;I24;J25). Данная сумма равна 10. Для того, чтобы закольцевать маршрут движения автопоезда из ПТЦ для сбора пожарных рукавов в условиях низких температур, проводится повторный поиск решения, добавив новое ограничение Е40≤9 (рис. 41). 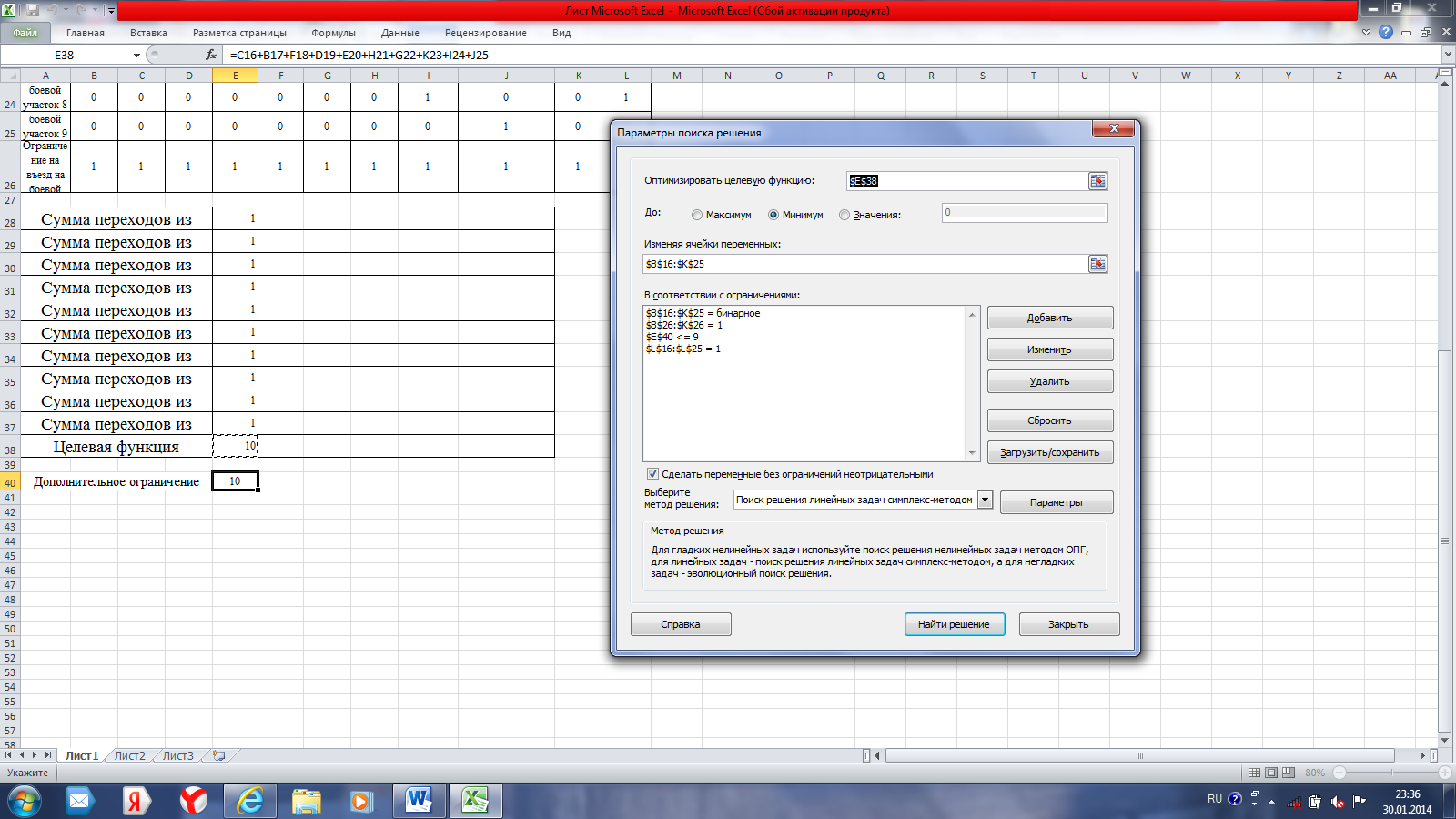 Рисунок 41 – Вид формы с дополнительными ограничениями для закольцевания маршрута движения Итоговый план объезда боевых участков на пожаре необходимо составить самостоятельно. Задание для самостоятельной работы Решить задачу при помощи табличного процессора MS Excel, используя функцию Поиск решения. Выполнить самостоятельную работу по произвольной матрице расстояний, включающей не менее 12 боевых участков. |
