Контрольная. Задача Обосновать выбор, описать метрологические характеристики и приемы применения средств измерений линейных размеров для заданных номинального значения и допусков отверстия и вала.
 Скачать 420.05 Kb. Скачать 420.05 Kb.
|
|
Задача 1. Обосновать выбор, описать метрологические характеристики и приемы применения средств измерений линейных размеров для заданных: номинального значения и допусков отверстия и вала. Сформировать условное обозначение, определить вид и систему образования посадки, построить схему посадки отверстия и вала и рассчитать основные характеристики посадки, предельно допустимые размеры и допуски сопрягаемых деталей. Исходные данные: 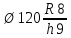 Решение: 1.1 Для измерения вала Ø120h9 с погрешностью, менее Для измерения отверстия Ø120R8 с погрешностью Таблица 1.1
Обоснование выбора СИ: Погрешность выбранного средства измерения не должна превышать допустимую погрещность измерения, таким образом для измерения вала Описание СИ: Нутромер При измерениях индикаторным нутромером его предварительно настраивают на измеряемый размер по микрометру, блоку плоскопараллельных концевых мер или калиброванному кольцу и после этого устанавливают на нуль. Настроенный нутромер осторожно вводят в измеряемое отверстие и небольшими покачиваниями (рис. 1.2, а) определяют отклонение стрелки от нулевого положения. Это и будет отклонение измеряемого размера от того, на который был настроен. В тех случаях, когда измерительный стержень индикаторной головки не может коснуться измеряемой поверхности, прибегают к специальным рычажным приспособлениям, соединенным с корпусом индикатора. Устройство этих приспособлений ясно из рисунка (рис. 1.2, б). 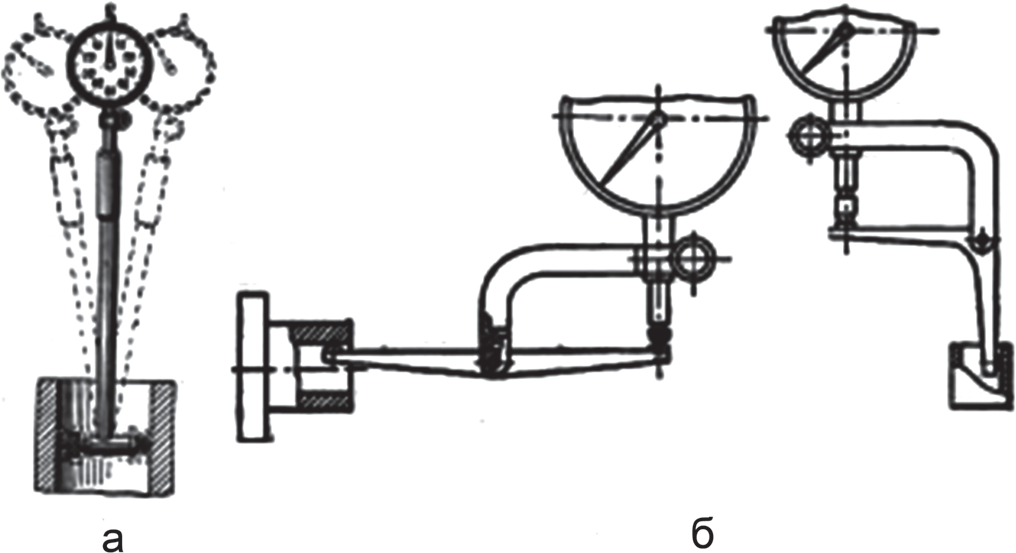 Рисунок 1.2 - Индикаторный нутромер (а) и рычажные приспособления к индикатору (б), применяемые для измерений в труднодоступных местах Микрометр Микрометры для наружных измерений (рис.1.3), микрометрические нутромеры и микрометрические глубиномеры относятся к микрометрическим инструментам. 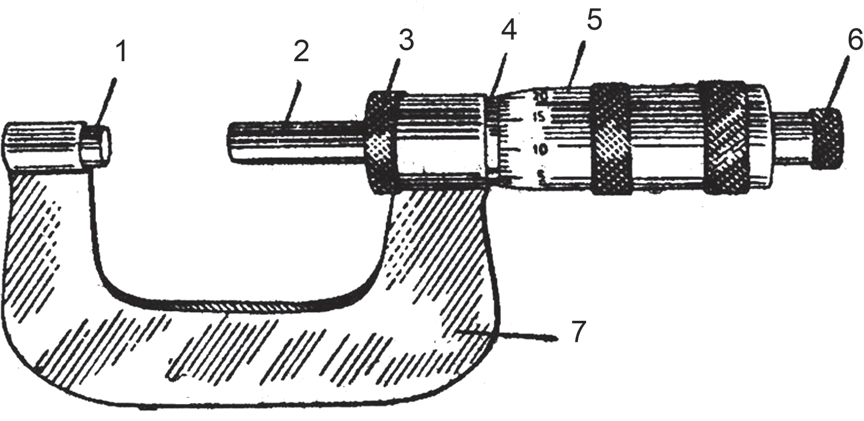 Рисунок 1.3 - Микрометр для наружных измерений: 1 — пятка; 2 — микрометрический винт; 3 — стопорная гайка; 4 — втулка; 5 — барабан; 6 — трещотка; 7 — скоба Отсчетное устройство микрометрических инструментов состоит из втулки 1 (рис.1.3, а) и барабанчика 2. На втулке по обе стороны продольной линии нанесены две шкалы с делениями через 1 мм так, что верхняя шкала сдвинута по отношению к нижней на 0,5 мм. На скошенном конце барабанчика имеется круговая шкала с 50 делениями. При вращении барабанчик перемещается вдоль втулки и за один оборот проходит путь, равный 0,5 мм. Следовательно, цена деления шкалы барабанчика равна 0,5:50=0,01 мм. При измерениях целое число миллиметров отсчитывают по нижней шкале, половины миллиметров — по верхней шкале втулки, а сотые доли миллиметра — по шкале барабанчика. Число сотых долей миллиметра отсчитывают по делению шкалы барабанчика, совпадающему с продольной риской на втулке. Номинальный размер: 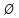 120 мм. 120 мм.Отклонение отверстия: ES = -0,054 мм (верхнее) EI = -0,108 мм (нижнее) Отклонения вала: es = 0 мм (верхнее) ei = -0,087 мм (нижнее) Предельные размеры: Наибольший предельный размер вала dmax: dmax= d + es = 120,0 + 0 = 120,000 мм Наименьший предельный размер вала dmin: dmin = d + ei = 120,0 + (-0,087) = 119,913 мм Наибольший предельный размер отверстия: Dmax = D + ES = 120,0 + (-0,054) = 119,946 мм Наименьший предельный размер отверстия: Dmln= D+ EI = 120,0 + (-0,108) = 119,892 мм Посадка переходная, в системе вала. Характеристика посадки: Максимальный натяг в соединении: Nmax= dmax - Dmin= 120,000 – 119,892 = 0,108 мм Максимальный зазор в соединении: Smax=Dmax- dmin= 119,946 – 119,913 = 0,033мм Допуски: Поле допуска вала: ITd= dmax – dmin = 120,000 – 119,913 = 0,087 мм Определим поле допуска отверстия: ITD = Dmax- Dmin = 119,946 – 119,892 = 0,054 мм Допуск посадки (натяга): ITSN =Nmax + Smax= 0,108 + 0,033 = 0,141 мм Проверка: ITSN = ITd + ITD = 0,087 + 0,054 = 0,141 мм Схема расположения полей допусков: 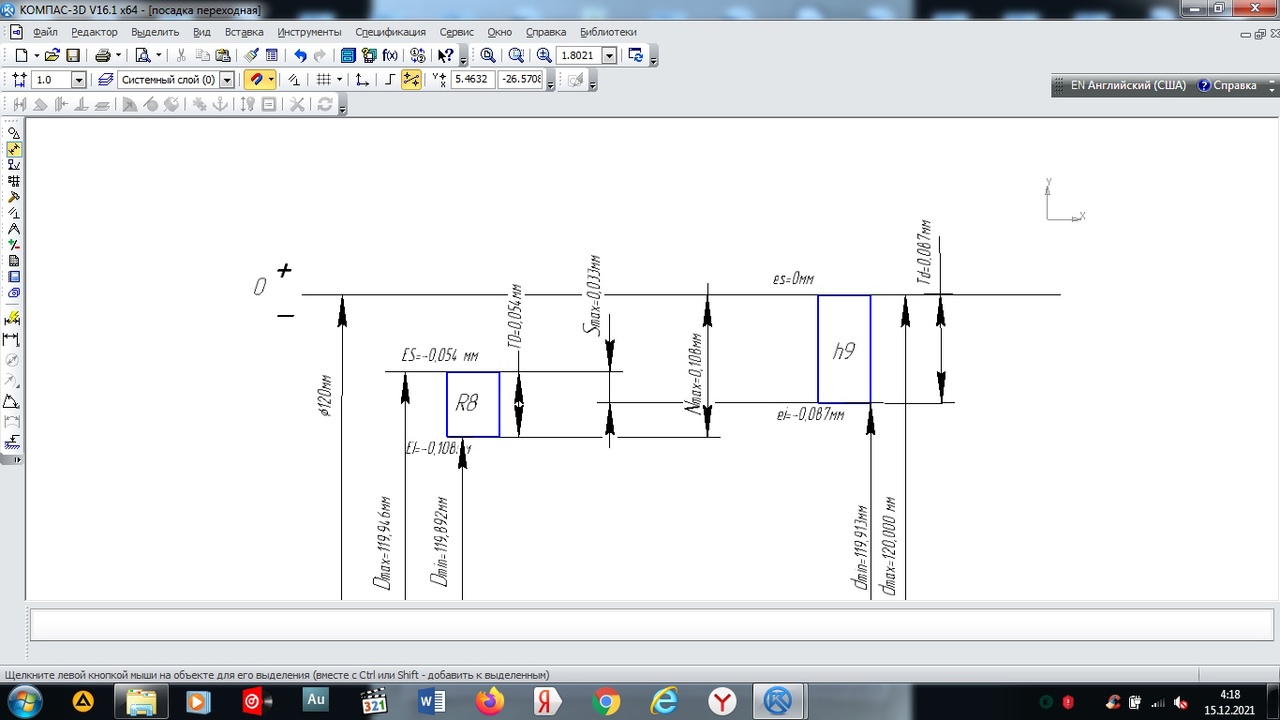 Рисунок 1.1 – Схема расположения полей допусков Определили в соответствии с классификацией вид измерений, выполняемых выбранным СИ: Вид измерения вала микрометром: однократные, необходимые, абсолютные, равноточные, статические, контактные, непосредственной оценки, прямые. Вид измерения отверстия нутромером однократные, необходимые, абсолютные, равноточные, статические, контактные, непосредственной оценки, прямые. Задача 2. Произведены прямые многократные измерения линейного размера. Результаты измерений представлены в виде отклонений от номинального значения. Требуется: Построить гистограмму эмпирического распределения. Проверить критерием Шарлье наличие и исключить имеющиеся промахи. Проверить гипотезу о соответствии эмпирического распределения нормальному закону Гаусса с помощью критерия Пирсона χ2. Построить доверительный интервал для результата многократных измерений. Исходные данные: Таблица 2.1
Таблица 2.2
Решение: 2.1. Проверили крайние (наибольший и наименьший) результаты измерений на наличие грубых погрешностей (промахов) с помощью критерия Шарлье. Для этого: 2.1.1. Рассчитали среднее арифметическое значение ( 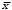 ) результатов измерений: ) результатов измерений: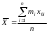 , ,где 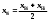 ; ; xвi и xнi – верхняя и нижняя границы каждого интервала, соответственно. 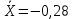 2.1.2. Рассчитали среднее квадратичное отклонение (СКО): 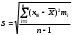 S = 1,6 2.1.3. Для крайнего результата измерений проверили неравенство: 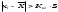 , ,где Кш – значения критерия Шарлье приведены в приложении А. Кш =2,58 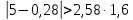 4,72 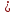 4,13 4,13Неравенство выполняется, следовательно, значение 5 является промахом, исключаем его из обработки. Пересчитываем среднее арифметическое и СКО: 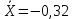 ; S = 1,5 ; S = 1,5Проверяем условие: 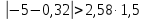 5,32 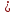 3,83 3,83Неравенство выполняется, следовательно, значение -5 является промахом, исключаем его из обработки. Пересчитываем среднее арифметическое и СКО: 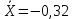 ; S = 1,5 ; S = 1,5Проверяем условие: 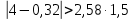 53,68 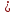 3,83 3,83Неравенство не выполняется, следовательно, значение промахом не является. Проверяем условие: 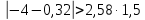 4,32 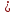 3,83 3,83Неравенство выполняется, следовательно, значение -4 является промахом, исключаем его из обработки. Пересчитываем среднее арифметическое и СКО: 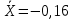 ; S = 1,39 ; S = 1,39Проверяем условие:  3,16 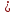 3,59 3,59Неравенство не выполняется, следовательно, значение промахом не является. Таким образом, исключили промахи с обоих концов ранжированного ряда. 2.2. Построили гистограмму эмпирического распределения без учета исключенных результатов измерений, являвшихся промахами. 2.2.1. Для каждого интервала определили эмпирическую (статистическую) вероятность попадания случайной измеряемой величины в i-й интервал (частость): 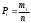 где mi ‒ число значений, попавших в i-й интервал (см. табл. 3); n ‒ общее число экспериментальных данных: 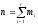 , где r ‒ число интервалов. , где r ‒ число интервалов.2.2.2. Построили гистограмму (рис. 2.1), которая представляет собой ступенчатую фигуру, состоящую из прямоугольников. 2.3. Проверили гипотезу о соответствии эмпирического распределения нормальному закону Гаусса. 2.3.1. Определили теоретическую вероятность попадания значений измеряемой величины в i-й интервал в соответствии с законом нормального распределения: PTi = Ф((xвi - 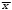 )/S) – Ф((xнi - )/S) – Ф((xнi -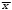 )/S), )/S),где Ф (***) – значение функции Лапласа по приложению Б. 2.3.2. Нанесли полученные значения теоретической вероятности на график (см.рис.2.1) и построили кривую теоретического распределения вероятности по нормальному закону. 2.3.3. Рассчитали для каждого интервала значение 2i: i2= 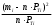 . .2.3.4. Результаты расчетов представили в таблице по установленной форме (Приложение Г). 2.3.5. Рассчитали эмпирическое значение 2: 2=  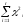 . .2.3.6. Полученное значение сравнили с табличным т2. По приложению В  для уровня значимости q= 1 – P и числа степеней свободы f = r ‒3. для уровня значимости q= 1 – P и числа степеней свободы f = r ‒3.т2=14,07 2.3.7. Сделать вывод о соответствии эмпирического распределения результатов измерений теоретическому нормальному закону по правилу: 2 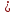 т2 гипотеза отклоняется. т2 гипотеза отклоняется.2.4. Определить доверительный интервал для результата многократных измерений: 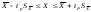 -0,57 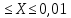 где tp=1,96 - коэффициент распределения Стьюдента при заданной доверительной вероятности Р и числе степеней свободы k= n – 1 (Приложение Д); 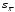 - среднее квадратичное отклонение среднего значения: - среднее квадратичное отклонение среднего значения: 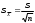 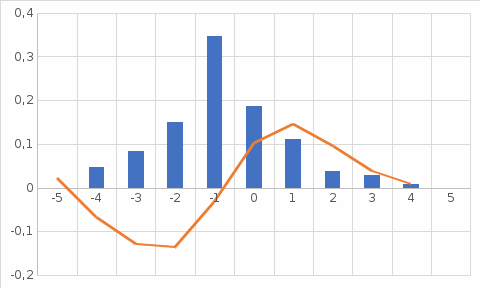 Рисунок 2.1 - Гистограмма и кривая теоретического распределения Расчетные данные для проверки гипотезы о нормальности распределения Таблица 2.3
Задача 3. Произведены многократные измерения двух параметров а1 и а2. Известна функциональная зависимость 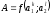 (табл. 4) для определения косвенно измеряемой величины. Значения параметров а1 и а2 приведены в таблице. (табл. 4) для определения косвенно измеряемой величины. Значения параметров а1 и а2 приведены в таблице. Требуется. Найти измеряемую косвенно с помощью функциональной зависимости величину и представить результат измерений в форме доверительного интервала с заданной доверительной вероятностью Р. Исходные данные: Таблица 3.1
Таблица 3.2
Рещение: 3.1. Рассчитали оценочное среднее арифметическое значение измеряемой величины  с учетом функциональной зависимости: с учетом функциональной зависимости: 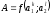 , где а1 и а2 – средние арифметические значения измеряемых аргументов, вычисляемые по формуле: , где а1 и а2 – средние арифметические значения измеряемых аргументов, вычисляемые по формуле: 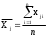 , , где хji ‒ измеряемое значение j-го аргумента; n ‒ число измерений; индексы k и l‒ показатели степени аргументов. 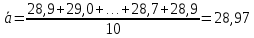 м м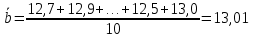 м м = =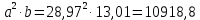 м3 м33.2. Рассчитали СКО среднего арифметического каждого аргумента: 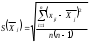 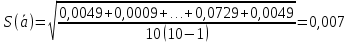 м м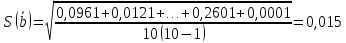 м м3.3.Рассчитали СКО среднего арифметического измеряемой величины: 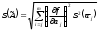 где 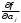 ‒ первая производная функции измеряемой величин по аj-му аргументу; m=2 ‒ число измеряемых аргументов. ‒ первая производная функции измеряемой величин по аj-му аргументу; m=2 ‒ число измеряемых аргументов.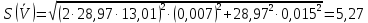 3.4. Вычислили остаточный член ряда Тейлора: 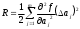 , ,где 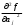 ‒ полный дифференциал второго порядка в частных производных функции f ; ‒ полный дифференциал второго порядка в частных производных функции f ; 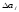 ‒ наибольшее отклонение измеренных значений aj-го аргумента от его среднего арифметического значения: ‒ наибольшее отклонение измеренных значений aj-го аргумента от его среднего арифметического значения:  . .R= 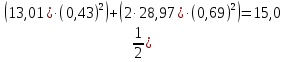 3.5. Установили влияние остаточного члена R на результат .измерений по условию: если R ≥ 0,8S(  ), на его значение увеличили значение ), на его значение увеличили значение . .3.6. Представили результат измерений А в форме доверительного интервала: 10933,8 – 2,685 5,27 < V < 10933,8 + 2,685 5,27 10919,65< V < 10947,95 где tp=2,685 - табличное значение критерия Стьюдента при заданной доверительной вероятности Р (Приложение Д). Задача 4. Определите, какое средство измерений предпочтительно применять для обеспечения большей точности результатов. Укажите пределы, в которых может находиться значение измеряемой величины при известных метрологических характеристиках применяемых средств измерений. Выразите размерность измеряемой величины через размерности основных величин системы SI. Исходные данные: Таблица 4.1
Таблица 4.2
Решение: 4.1. По условному обозначению класса точности определили вид погрешности, на основании которой он установлен. №1 – приведенная погрешность, 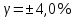 №2 – относительная погрешность, 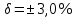 4.2. Определили предельные значения относительных погрешностей при измерении заданного значения величины каждым из двух СИ. №1 Найдем абсолютную погрешность, по формуле: 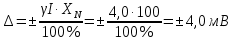 Значения относительной погрешности будем рассчитывать по формуле:  4.3. Сделали вывод о том, СИ №2 даст более точный результат. 4.4. Рассчитали предельные абсолютные погрешности при измерении заданной величины каждым из двух СИ. №1 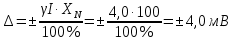 №2 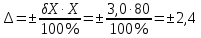 мВ мВ4.5. Вычислили границы двух интервалов значений результатов измерений заданной величины с учетом абсолютных погрешностей каждого СИ. №1 Х= (80 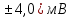 (76 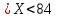 ) )№2 Х= (80 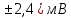 (77,6  ) )4.6. Выразили размерность измеряемой величины через размерности основных физических величин SI. 4.6.1. Дали определение физической величины. Электрическое напряжение - физическая величина, которая равна работе электрического поля по перемещению единичного заряда из одной точки в другую. 4.6.2. Раскрыли математической формулой ее взаимосвязь с основными величинами. U=A/q 4.6.3. Записали ее размерность в форме степенного одночлена, содержащего размерности основных величин SI. dimU=dim2l·dim1m·dim-3t·dim-1I = L2MT-3I-1 Список использованной литературы 1. Кошлякова И.Г., Сорочкина О. Ю., Закалин Е. Н. Теория и практика нормирования точности в машиностроении: учебное пособие/; Донской гос. технический ун-т. - Ростов-на Дону: ДГТУ, 2013. 2. Допуски и посадки. Справочник/Под ред. В.Д. Мягкова. - Л.: Машиностроение, 1982, ч.1. 3. ГОСТ 8.051-81 «Погрешности, допускаемые при измерении линейных размеров до 500 мм». 4. РД 50-98-86. Методические указания «Выбор универсальных средств измерений линейных размеров до 500 мм» (по применению ГОСТ 8.051-81). 5. Сергеев А.Г. Метрология: Учебник. – М., 2005. – 272 с. 6. Кошлякова И.Г., Ваганов В.А., Атоян Т.В. Практикум по метрологии и стандартизации. – Ростов н/Д: Издательский центр ДГТУ, 2013. – 214 с. 7. Маркин И.С.Основы теории обработки результатов измерений. - М.: Изд-во стандартов, 1991. – 268 с. 8. Маркин Н.С. Практикум по метрологии. - М.: Изд-во стандартов, 1994. – 214с. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 )/S
)/S
