задачи по статистике 2. Задача Образуют ли полную группу следующие группы событий
 Скачать 98 Kb. Скачать 98 Kb.
|
|
ПРИЛОЖЕНИЕ 2 Задача 1. Образуют ли полную группу следующие группы событий: a) Опыт — бросание монеты; события:
б) Опыт — бросание двух монет; события:
Задача 2. Являются ли несовместными следующие события: а) Опыт — два выстрела по мишени; события:
б) Опыт — два выстрела по мишени; события:
Задача 3. Являются ли равновозможными следующие события: а) Опыт — бросание неправильной (погнутой) монеты; события:
б) Опыт — выстрел по мишени; события:
Задача 4. Среди 1000 новорожденных оказалось 517 мальчиков. Найти частоту рождения мальчиков. Задача 5. В аптечке имеется 10 тюбиков пенициллина, 20 тюбиков биомицина, 40 тюбиков анальгина и 30 тюбиков амидопирина. Найти вероятность появления биомицина или анальгина при доставании тюбиков. Задача 6. Медицинская сестра обслуживает в палате четырех больных. Вероятность того, что в течение часа первый больной потребует внимания сестры Р(A) = 0,2, второй больной - Р(В) = 0,3, третий больной - P(С) = 0,25, четвертый больной - Р(D) = 0,1. Найти вероятность того, что в течение часа все больные потребуют к себе внимания сестры. Задача 7. В семье трое детей. Считая рождение мальчика и девочки равновероятными событиями, найти вероятность того, что в семье все мальчики. Задача 8. Вычислительная машина состоит из N блоков. Надежность (вероятность безотказной работы) в течение времени T первого блока равна P1, второго — P2 и т.д. Блоки отказывают независимо друг от друга. При отказе любого блока отказывает машина. Найти вероятность того, что машина откажет за время T. Задача 9. В партии 12 приборов, из них 3 бракованных. Найти вероятность того, что:
Зависимы ли эти события? Задача 10. При тестировании 2000 человек было обнаружено, что:
Задача 11. Во время эпидемии гриппа из 15 человек, доставленных в больницу с переломом, 5 оказались больны гриппом. В палату помещают по 4 человека. Найти вероятность того, что в палате окажутся:
Задача 12. Сигнальная лампочка прибора с вероятностью 0,1 перегорает при включении в сеть. Найти вероятность того, что она перегорит при втором включении. Задача 13. Студентка отвечает на вопросы, выбирая из 4 предложенных ответов 1 правильный ответ. Всего 6 вопросов. Какова вероятность ответить на все вопросы неверно? Задача 14. Гардеробщица выдала номерки одновременно 4-м лицам, сдавшим в гардероб свои куртки. После этого она перепутала все куртки и повесила их наугад. Найти вероятности следующих событий: а) каждый получит свою куртку; б) ровно три лица получат свои куртки. Задача 15. Студент пришел на экзамен, зная лишь 20 вопросов из 24. В билете три вопроса. Найти вероятность того, что ему в билете попадется хотя бы один вопрос, который он не знает. Задача 16. В семье двое детей. Найти вероятность того, что оба ребенка мальчики в предположении, что: а) старший ребенок – мальчик; б) по крайней мере, один из детей – мальчик. Задачи на формулу полной вероятности Задача 17. Имеются три коробки с шарами. В 1-й находится 5 белых и 3 черных, во второй – 4 белых и 4 черных шара, в третьей коробке – 8 белых шаров. Наугад выбирается одна из коробок. Из нее наугад извлекается 1 шар. Какова вероятность того, что он окажется черным? Задача 18. Прибор может работать в двух режимах:
Нормальный режим работы наблюдается в 80% всех случаев работы прибора; ненормальный — в 20%. Вероятность выхода прибора из строя за время t в нормальном режиме равна 0,1; в ненормальном — 0,7. Найти полную вероятность P выхода прибора из строя за время t. Задача 19. В ящике 8 зеленых и 5 желтых пуговиц. Вынимаются наугад две пуговицы. Какова вероятность того, что пуговицы будут одноцветными? Задача 20. Студент Петров собирается съездить к приятелю в другой город. К несчастью, его укачивает в транспорте. В автобусе его укачивает в 40% случаев, в самолете – в 30%, а в поезде – в 20% случаев. Зная, какую важную роль играет в жизни теория вероятностей, он решил поступить следующим образом. Если при бросании игральной кости выпадет четное число, то он поедет автобусом, если выпадет цифра 5, то он выбирает самолет, во всех остальных случаях он едет поездом. Оцените вероятность того, что студента Петрова укачает, если результат бросания кости еще неизвестен. Задачи на формулу Байеса Задача 21. Редкая и тяжелая форма анемии встречается в 1 случае на 1000 пациентов. Проведя простой диагностический тест, можно получить следующие результаты:
Один очень впечатлительный гражданин, подозревая у себя это заболевание, прошел тестирование. Результат теста – положительная реакция. Врач сказал пациенту, что он болен. Правильно ли врач поставил диагноз? Найдите вероятность того, что пациент действительно болен. Задача 22. В группе из 10 студентов, пришедших на экзамен, 3 подготовленных отлично, 4 — хорошо, 2 — посредственно и 1 — плохо. В экзаменационных билетах имеется 20 вопросов. Отлично подготовленный студент может ответить на все 20 вопросов, хорошо подготовленный — на 16, посредственно — на 10, плохо — на 5. Вызванный наугад студент ответил на 3 произвольно заданных вопроса. Найти вероятность того, что этот студент подготовлен: а) отлично; б) плохо. Задача 23. Предположим, что в условиях задачи 20 стало известно, что студента Петрова укачало. Найти вероятность того, что он ехал на автобусе. Задача 24. Пассажир может обратиться за получением билета в одну из трех касс. Вероятности обращения в каждую кассу зависят от местоположения и равны cоответственно p1, p2, p3. Вероятность того, что к моменту прихода пассажира имеющиеся в кассе билеты будут распроданы, равна для первой кассы P1, для второй — P2, для третьей — P3. Пассажир направился за билетом в одну из касс и приобрел билет. Найти вероятность того, что это была первая касса. Задачи на распределения случайных величин Задача 25. Найдите распределение случайной величины, образующейся при бросании правильного однородного куба с пронумерованными гранями 1, 2 , 3, 4, 5, 6. Составить таблицу распределения, построить многоугольник распределения. Вычислить математическое ожидание, дисперсию, среднеквадратичное отклонение. Задача 26. Измерена частота пульса у 100 человек. Получены следующие результаты:
Построить многоугольник распределения. Вычислить математическое ожидание, дисперсию, среднеквадратичное отклонение. Задача 27. О влиянии фармакологического препарата судили по изменению массы лабораторных животных, которым в течение недели вводили препарат. За неделю изменения веса составили (M — масса в г, P — вероятность):
Найти математическое ожидание, дисперсию, среднее квадратичное отклонение прибавки массы. Задача 28. Функция плотности распределения f(x) задана следующим образом: 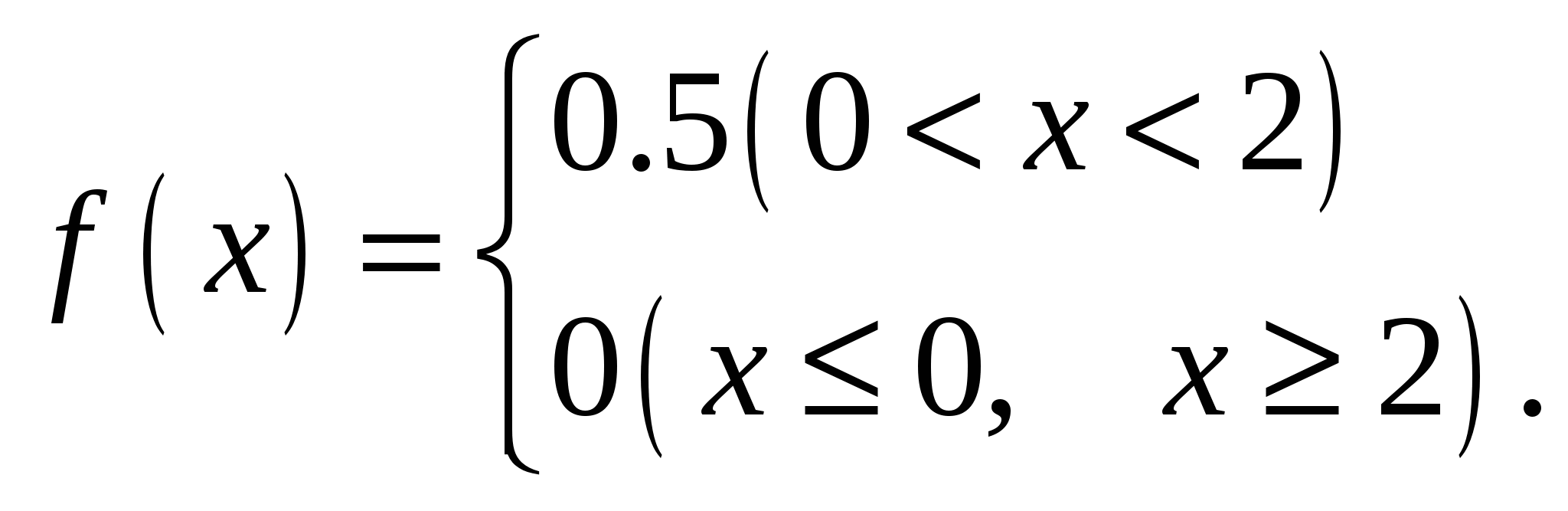 Найти математическое ожидание, дисперсию и среднеквадратичное отклонение. Задача 29. Н 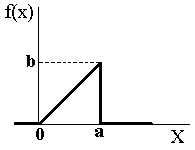 айдите математическое ожидание и дисперсию случайной величины, представленной ниже графиком на рисунке. Задачи на биномиальное распределение Задача 30. Исходя из многолетних наблюдений, вызов врача в некоторый дом оценивается вероятностью 0,4. Найдите вероятность того, что из пяти вызовов врача два вызова будут в данный дом. Задача 31. Из десяти облигаций в тираже в среднем выигрывает одна. Какова вероятность того, что из двадцати облигаций выиграет только одна? Задача 32. Предположим, что с вероятностью 0,6 любой человек верит в сказку о загробной жизни. Какова вероятность того, что из 5 человек, услышавших эту сказку, трое верят в загробную жизнь? Задача 33. Взяты образцы крови у жителей города N. Вероятность обнаружить в крови свинец составляет 0,3. Какова вероятность того, что у четверых из 10 человек, прошедших тестирование, обнаружен в крови свинец? Задача 34. Вероятность благополучного выздоровления после сложной операции на сердце составляет 0,85. Какова вероятность того, что из 7 пациентов 5 человек выживут после этой операции? Задачи на распределение Пуассона Задача 35. Предположим, что на 500 человек приходится 1 алкоголик. Найти вероятность того, что среди 9000 человек будет 7 алкоголиков. Задача 36. Вычислить вероятности обслуживания в день от 0 до 15 пациентов, если известно, что в среднем на прием к врачу приходит 6 пациентов в день. Составить таблицу распределения и построить график (многоугольник распределения). Задачи на равномерное распределение Задача 37. По результатам 10-летних наблюдений за количеством зайцев, попавших под машины на участке лесной дороги длиной в 8 км, было установлено, что эта величина (число зайцев) подчиняется равномерному распределению. Найти вероятность того, что очередной заяц попадет под машину между началом участка и 2-м километром. Задача 38. В условиях предыдущей задачи найти вероятность того, что очередное дорожно-транспортное происшествие с участием зайца произойдет точно на 4-м километре участка. Задачи на нормальное распределение Задача 39. Нормальный закон распределения задан в форме уравнения: 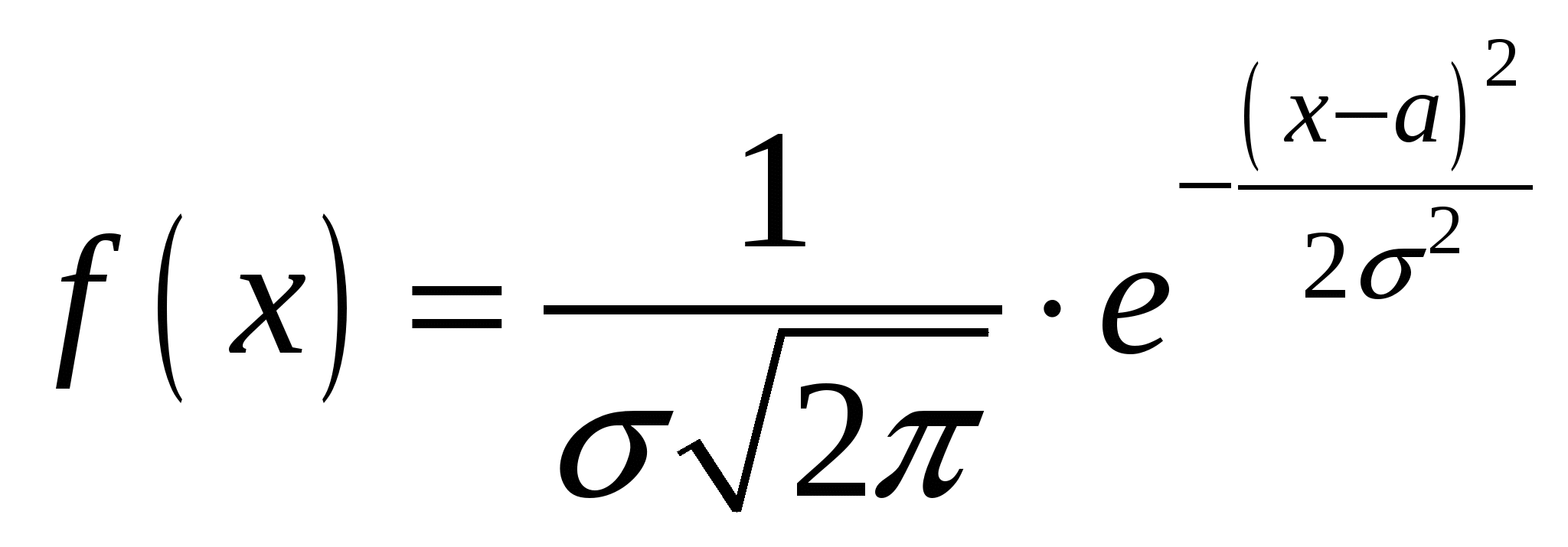 . .Какова вероятность того, что случайная величина примет значения x<a? x>a? Задача 40. В нормальном законе распределения a = 2, σ = 4. Чему равно x, если вероятность того, что случайная величина принимает значения меньше x, равна 3/4? Задача 41. Проведены точные измерения дозированного медицинского препарата, предназначенного для инъекций и содержащегося в ампулах по 1 мл в каждой ампуле, с целью уточнения влияния количества вводимого препарата на лечебный эффект. При проверке 12 ампул получили следующие результаты (в мл): 0,97; 1,07; 1,02; 1,04; 0,97; 0,96; 1,03; 1,05; 0,96; 0,97; 1,05; 1,01. Считая, что распределение подчиняется нормальному закону, определить вероятность того, что в ампуле меньше одного миллилитра раствора. Задача 42. Анализ веса 100 новорожденных показал, что у них в интервале от 1,75 до 2,25 (со средним весом 2 кг) попало 5 новорожденных; со средним весом 2,5 кг попало 25 новорожденных, со средним весом 3 кг — 40, 3,5 кг — 25 и 4 кг - 5 новорожденных. Совпадает ли это распределение с нормальным распределением Гаусса? Определить по полученным данным вероятность рождения недоношенного ребенка (m 2.4 кг). Задачи на распределение Стьюдента Задача 43. Измерение веса девочек в возрасте 10 лет дало следующие результаты :
Найти среднее арифметическое значение веса девочек, стандартное отклонение и ошибку среднего арифметического для PD=0,9. Задача 44. Пять измерений относительной вязкости крови человека дали следующие результаты: 4,80; 4,70; 4,85; 4,75; 4,90. Найти среднее значение, стандартное отклонение и ошибку среднего арифметического. Задача 45. Определить среднее значение и стандартное отклонение по данным 20 измерений максимального кровяного давления у одного больного за период болезни : 98, 160, 136, 128, 130, 114, 123, 134, 128, 107, 123, 125, 129, 132, 154, 115, 126, 132, 136, 130. Задачи на обработку прямых и косвенных измерений Задача 46. Десять измерений диаметра капилляра в стенке легочных альвеол дали следующие результаты(в мм): 2.83; 2.82; 2.81; 2.85; 2.87; 2.86; 2.83; 2.85; 2.83; 2.84. Провести обработку серии этих измерений для PD=0,95. Задача 47. Проведены измерения спектральной чувствительности уха на пороге слышимости. Уровень слышимости (L, дБ) измерялся на каждой частоте три раза. Получены следующие результаты:
Провести обработку результатов измерений для PD=0,9. Построить график зависимости уровня интенсивности от частоты с указанием доверительных интервалов. Задача 48. Провести обработку результатов измерений лабораторной работы «Изучение аппарата УВЧ» По классу точности миллиамперметра вычислить систематическую ошибку для измерения силы тока (см. задание 1). Ошибку в измерении температуры принять равной половине цены наименьшего деления термометра (см. задание 2). По результатам построить график с указанием доверительных интервалов. Задание 1. Изучение распределения поля УВЧ.
Класс точности миллиамперметра — 1,5. Предел шкалы — 200 мА. Задание 2. Исследование процесса нагревания диэлектрика и электролита.
Задачи на проверку статистических гипотез Задача 49. Измерена некоторая случайная величина Х. Получены следующие результаты: 12, 15, 18. По критерию Стьюдента проверить, достоверно ли полученное значение среднего арифметического. PD=0,95. Задача 50. Для сравнения активностей двух аналогичных препаратов были проведены две серии испытаний, в каждой из которых использовалось семь животных. Результаты приведены в таблице:
Следует ли отбрасывать нулевую гипотезу? Проверку провести по критерию Стьюдента для PD=0,95 и PD=0,99. Задача 51. Исследовалось влияние лекарственного препарата на величину некоторого параметра.
Используя критерий Стьюдента, проверить достоверно ли различие между средними значениями для контрольной и опытной групп. PD=0,95. Задача 52. Исследовалось влияние физической нагрузки на некоторый параметр X. Получены следующие результаты:
По критерию Стьюдента выяснить, достоверно ли влияние физической нагрузки для уровня значимости 0,95. Задача 53.(Дисперсионный анализ). Ниже приводятся данные о содержании иммуноглобулина lgA в сыворотке крови (в мг %) у больных пяти возрастных групп:
Предполагая, что выборки получены из нормально распределенных генеральных совокупностей с равными дисперсиями, проверить гипотезу о равенстве средних значений. Принять =0,05. Задача 54 (Дисперсионный анализ). На химико-фармацевтическом заводе разработаны два новых варианта технологического процесса. Чтобы оценить, как изменится дневная производительность при переходе на работу по новым вариантам технологического процесса, завод в течение 10 дней работает по каждому варианту, включая существующий вариант. Дневная производительность завода (в условных единицах) приводится в таблице:
Для уровня значимости =0,05 проверить, отличаются ли средние значения производительности для приведенных данных. Считать, что выборки получены из нормально распределенных генеральных совокупностей с равными дисперсиями. Задача 55 (Дисперсионный анализ). Время химической реакции при различном содержании катализатора распределилось следующим образом (в секундах):
Для уровня значимости =0,05 проверить, зависит ли время химической реакции от содержания катализатора. Считать, что выборки получены из нормально распределенных генеральных совокупностей с равными дисперсиями. Задача 56. Один из видов предпосевной обработки семян дал следующие изменения урожайностей.
Проверить по критерию Вилкоксона для уровня значимости =0,05 оказалась ли эффективной обработка семян. Задача 57. Проделанный одновременно (см. задача 56) другой вид предпосевной обработки семян дал результаты, которые сравниваются с тем же контролем, что и в предыдущей задаче.
По критерию Вилкоксона проверить для уровня значимости =0,05 оказалась ли эффективной данная обработка семян. Задача 58. Даны две выборки:
По критерию Манна-Уитни для уровня значимости =0,05 проверить, есть ли различие между выборками. Задача 59. Изучалось действие различных лекарственных препаратов на двух группах животных. Получены следующие результаты:
По критерию Манна-Уитни для уровня значимости =0,05 выяснить, значима ли разница между действием этих препаратов. Задачи на корреляционный и регрессионный анализ Задача 60. Частота пульса (X) и максимальное артериальное давление (Y) у детей разного возраста составляли:
Найти коэффициент корреляции и оценить его достоверность для уровня значимости 0,05. Задача 61. Количество рождений (X) и смертей (Y) на 100 человек населения в некотором районе (за каждые 5 лет):
Найти коэффициент корреляции и оценить его достоверность для уровня значимости 0,05. Задача 62. Вычислить коэффициенты корреляции между массой тела (х) в кг и весом головного мозга (у) в % для разных выборок и сравнить:
Задача 63. Цветные диски, имевшие порядок оттенков 1, 2, …, 15, были расположены испытуемым в следующем порядке: 7, 4, 2, 3, 1, 10, 6, 8, 9, 5, 11, 15, 14, 12, 13 Очевидно, что показатель корреляции между действительными и наблюдаемыми рангами будет характеризовать способность испытуемого различать оттенки цветов. Найти этот показатель. Что можно сказать о способности испытуемого различать цвета? Задача 64. Бегуны, ранги которых при построении по росту были 1, 2,…, 10, заняли на состязаниях места: 6, 5, 1, 4, 2, 7, 8, 10, 3, 9. По критерию ранговой корреляции оценить, как велика корреляция между ростом и быстротой бега? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
