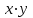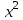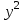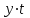РГР ПО СИС АНАЛИЗУ. РГР. Задача Оценка согласованности мнений экспертов 3
 Скачать 106.19 Kb. Скачать 106.19 Kb.
|
|
СОДЕРЖАНИЕ
1 Задача 1. Оценка согласованности мнений экспертов Вариант 9 Задание. Анализируются возможные направления повышения эффективности работы энергосбытовой компании. Исходные данные приведены в таблице 1. Оценить согласованность мнений экспертов с помощью коэффициента конкордации. Сделать выводы. Таблица 1 - Экспертная оценка направлений повышения эффективности работы энергосбытовой комапнии
РЕШЕНИЕ Определим степень согласованности мнений пяти экспертов по результатам ранжирования пяти направлений повышения эффективности работы энергосбытовой компании. Для этого используем коэффициент конкордации. Коэффициент конкордации определяется по формуле: 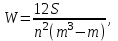 где S – сумма квадратов отклонений всех оценок рангов каждого объекта экспертизы от среднего значения; n – число экспертов; m – число объектов экспертизы. Вспомогательные расчеты представим в таблице 2. Таблица 2 – Данные для оценки согласованности мнения экспертов
Среднеарифметическое число рангов находится как отношение суммы рангов к числу объектов экспертизы (63/5) и составляет 12,6. Итак, 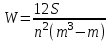 = =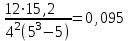 Коэффициент конкордации изменяется в диапазоне от 0 до 1 (0 – полная несогласованность, 1 – полное единодушие). Вывод: Коэффициент конкордации составил: W =0,095 Следовательно, степень согласованности мнений экспертов по возможным направлениям повышения эффективности работы энергосбытовой компании низкий. Задача 2. Применение метода наименьших квадратов в системном анализе. Вариант 25 Задание. Используя метод наименьших квадратов и предполагая линейную зависимость потребления молока и молочных продуктов на душу населения (в год; килограммов) от среднедушевых денежных доходов населения (в месяц; рублей) построить уравнение парной линейной регрессии; определить коэффициент корреляции и детерминации; оценить значимость уравнения регрессии. Исходные данные для анализа представлены в таблице 3. (число наблюдений 7) Таблица 3. Исходные данные для анализа. (https://rosstat.gov.ru/bgd/regl/b19_14p/Main.htm)
РЕШЕНИЕ: 1 Зависимый (результативный) признак (y) ПОТРЕБЛЕНИЕ, МОЛОКА И МОЛОЧНЫХ ПРОДУКТОВ на душу населения (в год; килограммов) Независимый (факторный) признак (х) СРЕДНЕДУШЕВЫЕ ДЕНЕЖНЫЕ ДОХОДЫ НАСЕЛЕНИЯ (в месяц; рублей) Уравнение линейной регрессии имеет вид: 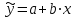 , ,где 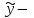 зависимая (выровненная) переменная; зависимая (выровненная) переменная;x – независимая переменная (факторный признак); a, b – параметры уравнения регрессии (а – значение 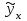 при x= 0, экономического содержания не имеет; b – коэффициент регрессии). при x= 0, экономического содержания не имеет; b – коэффициент регрессии).Для написания уравнения регрессии нам необходимо найти параметры a и b. Для определения параметров a и b уравнения регрессии применим метод наименьших квадратов (МНК). Система нормальных уравнений имеет вид: 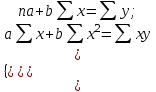 где n – количество наблюдений. Расчет значений параметров a и b линейной функции выполнен на ЭВМ с помощью команды Microsoft Excel: Данные / Анализ данных / Регрессия(Приложение А). Для решения системы уравнений построим вспомогательную таблицу 4. Таблица 4 – Вспомогательная таблица для расчета параметров уравнения
Коэффициентам уравнения линейной регрессии можно придать экономический смысл. Коэффициент уравнения регрессии показывает, на сколько единиц изменится результативный признак при изменении факторного на 1 единицу. (Например, коэффициент b = 0,00134137 показывает среднее изменение результативного показателя (в единицах измерения Y) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 0,00134137). Связь между у и x определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе - обратная). В нашем примере (b = 0,00134137) связь прямая. 2 Для оценки степени тесноты связи вычисляются следующие коэффициенты: а) коэффициент корреляции: 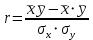 = =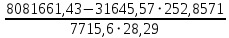 = 0,365 = 0,365где средние квадратические отклонения: 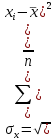 = = 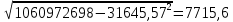 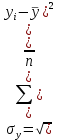 = = 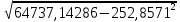 = 28,29 = 28,29Коэффициент корреляции показывает тесноту линейной связи между результативным (у) и факторным (х) признаками. Коэффициент корреляции может принимать значения 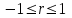 . Если . Если 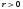 , то связь между признаками прямая, если , то связь между признаками прямая, если 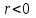 - связь обратная. - связь обратная.Для оценки тесноты связи используют шкалу: до  0,3 – связь отсутствует или очень слабая; 0,3 – связь отсутствует или очень слабая;от  0,3 до 0,3 до  0,5 – связь слабая; 0,5 – связь слабая;от  0,5 до 0,5 до  0,7 – связь умеренная; 0,7 – связь умеренная;от  0,7 до 0,7 до  1,0 – связь сильная. 1,0 – связь сильная.Вывод : Коэффициент корреляции равен 0<0,365, связь является прямой и слабой б) коэффициент детерминации: D = 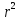 = = =0,1332 =0,1332Значение коэффициента детерминации изменяется от 0 до 1 и показывает, на сколько процентов вариация результативного признака определяется вариацией фактора, включенного в уравнение. (Например, D=0,133 значит, вариация результата Y - потребление молока и молочных продуктов на 1,332 % определяется вариацией фактора, включенного в уравнение, т.е. среднедушевых денежных доходов населения) Чем ближе значение коэффициента детерминации к 1, тем функция является более адекватной по данному показателю. Вывод: Среднедушевые денежные доходы высокие. 3) Для оценки значимости уравнения регрессии рассчитывается F – критерий Фишера: 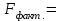 = = 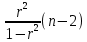 = =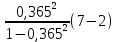 = 0,768 = 0,768Для оценки значимости уравнения регрессии 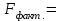 0,768. Сравнивается с Fтабл. при 0,768. Сравнивается с Fтабл. при 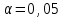 , , 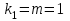 , , 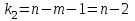 Fтабл = 6,61 Если Fтабл. > Fфакт.. уравнение регрессии незначимо, статистически ненадежно и не может быть использовано для прогнозирования. Вывод: Уравнение регрессии незначимо, статистически ненадежно и не может быть использовано для прогнозирования. Задача 3. Прогнозирование по методу экстраполяции Вариант 25 Задание. Используя метод экстраполяции и предполагая линейную зависимость потребления электроэнергии по субъектам Российской Федерации от времени: построить уравнение линейного тренда и получить прогноз на 2 года вперед (2020, 2021 гг.). Отразить фактические и расчетные значения показателей потребления (включая прогноз) на графике. Исходные данные представлены в таблице 5. Потребление электроэнергии по субъектам Российской Федерации, (млн.кВт.час)
Таблица 5 – Исходные данные для прогнозирования по варианту № 25
РЕШЕНИЕ: Для определения параметров уравнения тренда 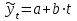 построим вспомогательную таблицу 6. построим вспомогательную таблицу 6.Таблица 6 – Вспомогательная таблица для прогнозирования Потребление электроэнергии по субъектам Российской Федерации, (млн.кВт.час)
*Y расчетное рассчитывается после нахождения параметров a и b, и определения уравнения тренда, путем подставления в полученное уравнение тренда соответствующего номера года. Параметры a и b находим из системы нормальных уравнений метода наименьших квадратов, которая имеет вид: 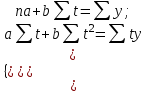 В данном примере 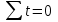 , поэтому вычисления параметров a и b упрощаются: , поэтому вычисления параметров a и b упрощаются: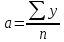 = = 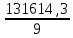 = 14623,81 = 14623,81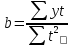 = =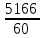 = 86.1 = 86.1Итак, полученное уравнение линейного тренда имеет вид: 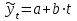 . == 14623,81+86.1*t . == 14623,81+86.1*tВывод: В самом начале наблюдается резкое увеличение и резкий спад. Дальше наблюдается плавное увеличение и плавный спад. Сделаем прогноз на два года (2020 и 2021 гг), используя полученное уравнение тренда 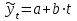 =14623,81+86.1*t, =14623,81+86.1*t, Прогноз на 2020 год (5)__ 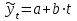 = 14623,81+86.1*5=15054,1 = 14623,81+86.1*5=15054,1 Прогноз на 2021 год: (6)_ _ 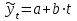 =14623,81+86.1*6=15140,41 =14623,81+86.1*6=15140,41 Фактические и расчетные значения показателя представим на графике 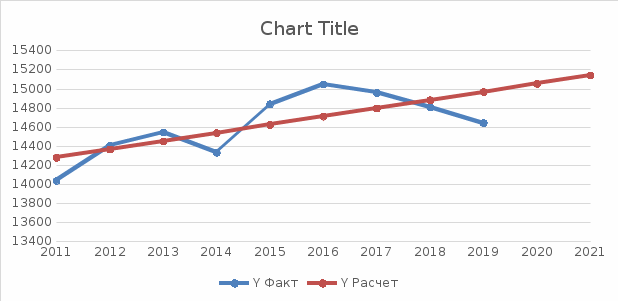 Вывод: За последние 9 лет наблюдается тенденция к росту потребления электроэнергии в млн кВат раз при сохранении данной тенденции в 2020 году этот показатель составит 15054,1 и в 2021 году составит 15140,41. БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1 Антонов, А. В. Системный анализ : учебник / А. В. Антонов. – 4-е изд., перераб. и доп. – Москва : ИНФРА-М, 2018. – 366 с. – Режим доступа: http://znanium.com/bookread2.php?book=973927. 2 Анфилатов, В. С. Системный анализ в управлении : учеб. пособие / В. С. Анфилатов, А. А. Емельянов, А. А. Кукушкин. – М. : Финансы и статистика, 2006. – 367 с. 3 Вдовин, В. М. Теория систем и системный анализ : учебник / В. М. Вдовин, Л. Е. Суркова, В. А. Валентинов. – 3-е изд. – Москва : Дашков и К, 2014. – 643 с. 4 Волкова, В. Н. Теория систем и системный анализ: учебник / В. Н. Волкова, А. А. Денисов. – 2-е изд., перераб. и доп. – Москва : Юрайт, 2013. – 616 с. 5 Козлов, В. Н. Системный анализ, оптимизация и принятие решений : учебное пособие: рек. УМО по образованию / В. Н. Козлов ; Санкт-Петербургский гос. политехн. ун-т. – М. : Проспект, 2010. – 173 с. 6 Корнев, Г. Н. Системный анализ : учебник / Г. Н. .Корнев, В. Б. Яковлев – М.: ИЦ РИОР, НИЦ ИНФРА-М, 2016. – 308 с. – Режим доступа: http://znanium.com/bookread2.php?book=538715 7 Кузнецов, В. А. Системный анализ, оптимизация и принятие решений: учебник для студентов высших учебных заведений / В. А. Кузнецов, А. А. Черепахин. – Москва : КУРС : ИНФРА-М, 2017. – 256 с. – Режим доступа: http://znanium.com/bookread2.php?book=636142. 8 Системный анализ : учебное пособие для практических занятий и самостоятельной работы студентов / Е. Г. Смотрова. – Волгоград: Волгоградский ГАУ, 2015. – 152 с. – Режим доступа: http://znanium.com/bookread2.php?book=615284. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||