Задача 1 с балкой №20. Задача Определение перемещений в балках при прямом изгибе
 Скачать 1.12 Mb. Скачать 1.12 Mb.
|
Задача 1. Определение перемещений в балках при прямом изгибе.Задание. Для балки по схеме, изображённой на рисунке 1.1, при числовых значениях нагрузок и размеров, представленных в таблице 1.1, требуется:
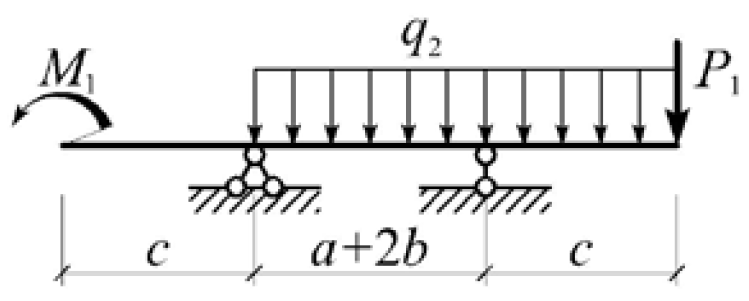 Рисунок 1.1 – Расчётная схема Таблица 1 – Исходные данные к задаче 1
Решение. 1. Определяем опорные реакции из условия равновесия. 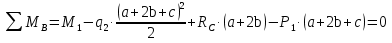 ; ;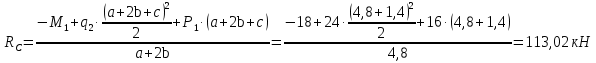 ; ;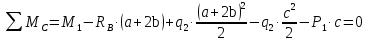 ; ;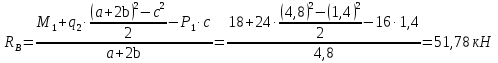 . .Проверка: 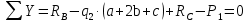 ; ;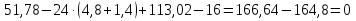 . .2. Построение эпюр внутренних усилий 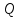 и и 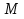 . .Для построения эпюр внутренних силовых факторов рассмотрим три произвольных сечения на участках 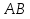 , , 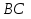 и и 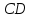 (рисунок 1.2, а). (рисунок 1.2, а).Участок 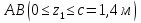 : :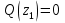 ; ;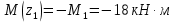 . .Участок 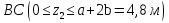 : :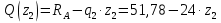 ; ;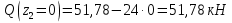 . .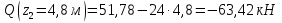 . .Найдём 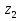 , при котором , при котором 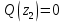 : :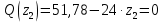 ; ;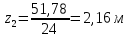 . .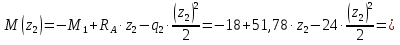 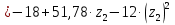 ; ;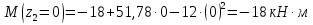 ; ;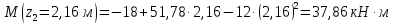 ; ;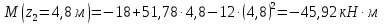 . .Участок 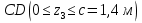 : :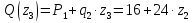 ; ;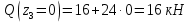 . .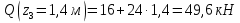 . .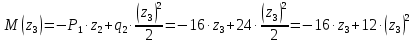 ; ;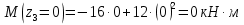 ; ;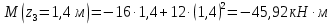 . .По полученным данным строим эпюры перерезывающей силы и изгибающего момента (рисунке 1.2, б, в).  Рисунок 1.2 3. Подбор сечения. По эпюре 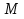 находим, что опасное сечение находится в сечении, где находим, что опасное сечение находится в сечении, где 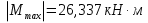 . .Из условия прочности находим требуемый момент сопротивления сечению материала: 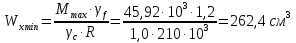 . .По ГОСТ 8239-89 выбираем двутавр №24 со следующими параметрами: 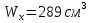 ; ; 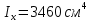 . .4. Определение значений прогибов 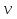 и углов поворота и углов поворота 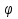 поперечных сечений в характерных точках по длине балки. поперечных сечений в характерных точках по длине балки.Составим выражение для прогиба балки в пределах трех характерных участков. 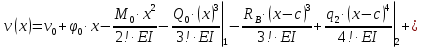 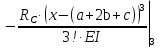 ; ;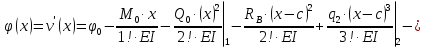 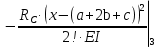 . .Начальные параметры равны: 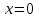 ; ;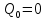 ; ; 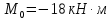 . .Для определения неизвестных параметров 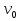 и и 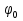 используем граничные условия: используем граничные условия: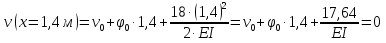 ; ;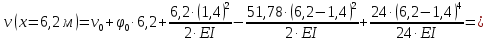 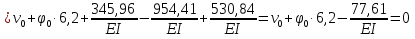 ; ;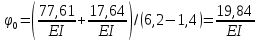 ; ;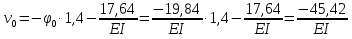 . . Запишем окончательные выражения для 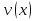 и и 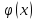 . .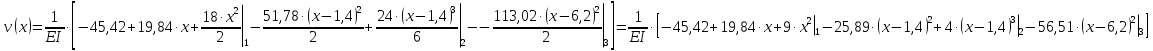 ; ;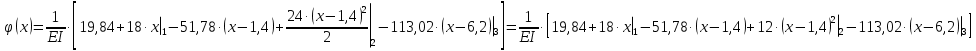 . .Вычислим значения 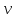 и и 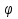 в характерных сечениях балки. в характерных сечениях балки.Сечение 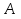 : :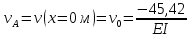 ; ;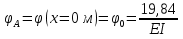 . .Сечение 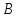 : :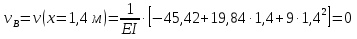 ; ;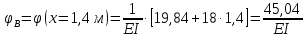 . .Сечение 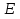 : :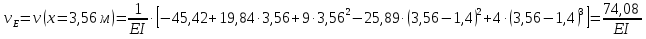 ; ;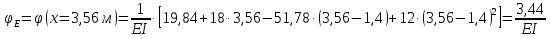 . .Сечение 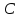 : :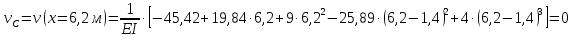 ; ;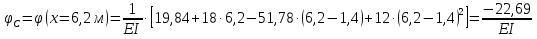 . .Сечение 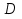 : :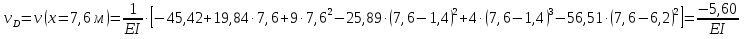 ; ;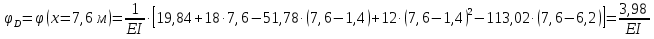 . .5. Метод Мора. Вычислим значения 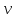 и и 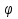 в характерных сечениях балки с помощью метода Мора. в характерных сечениях балки с помощью метода Мора.Построим единичные эпюры изгибающих моментов (рисунок 1.3 и 1.4) и вычислим интегралы Мора с помощью правила А.К. Верещагина, то есть «перемножим» единичные эпюры с эпюрой моментов от действия заданных нагрузок.  Рисунок 1.3 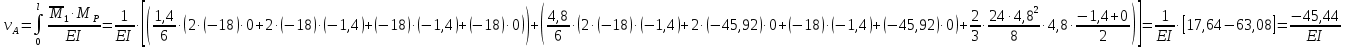 ; ;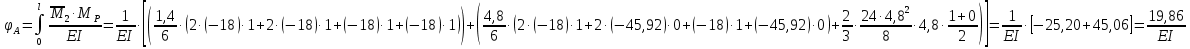 . .Сечение 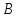 : :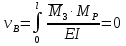 ; ;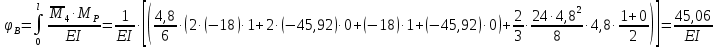 . . Рисунок 1.4 Сечение 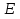 : :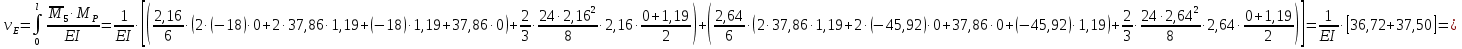 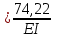 ; ;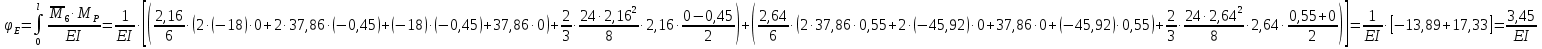 . .Сечение 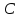 : :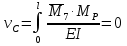 ; ;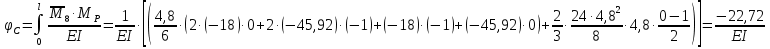 . .Сечение 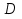 : :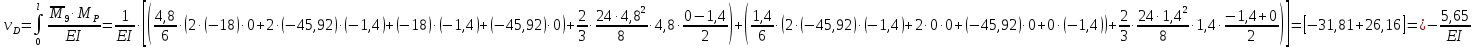 ; ;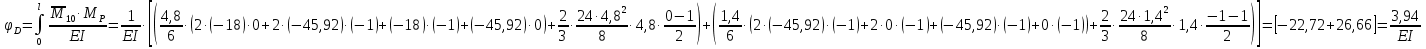 . .6. Строим эпюры 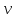 и и 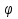 . .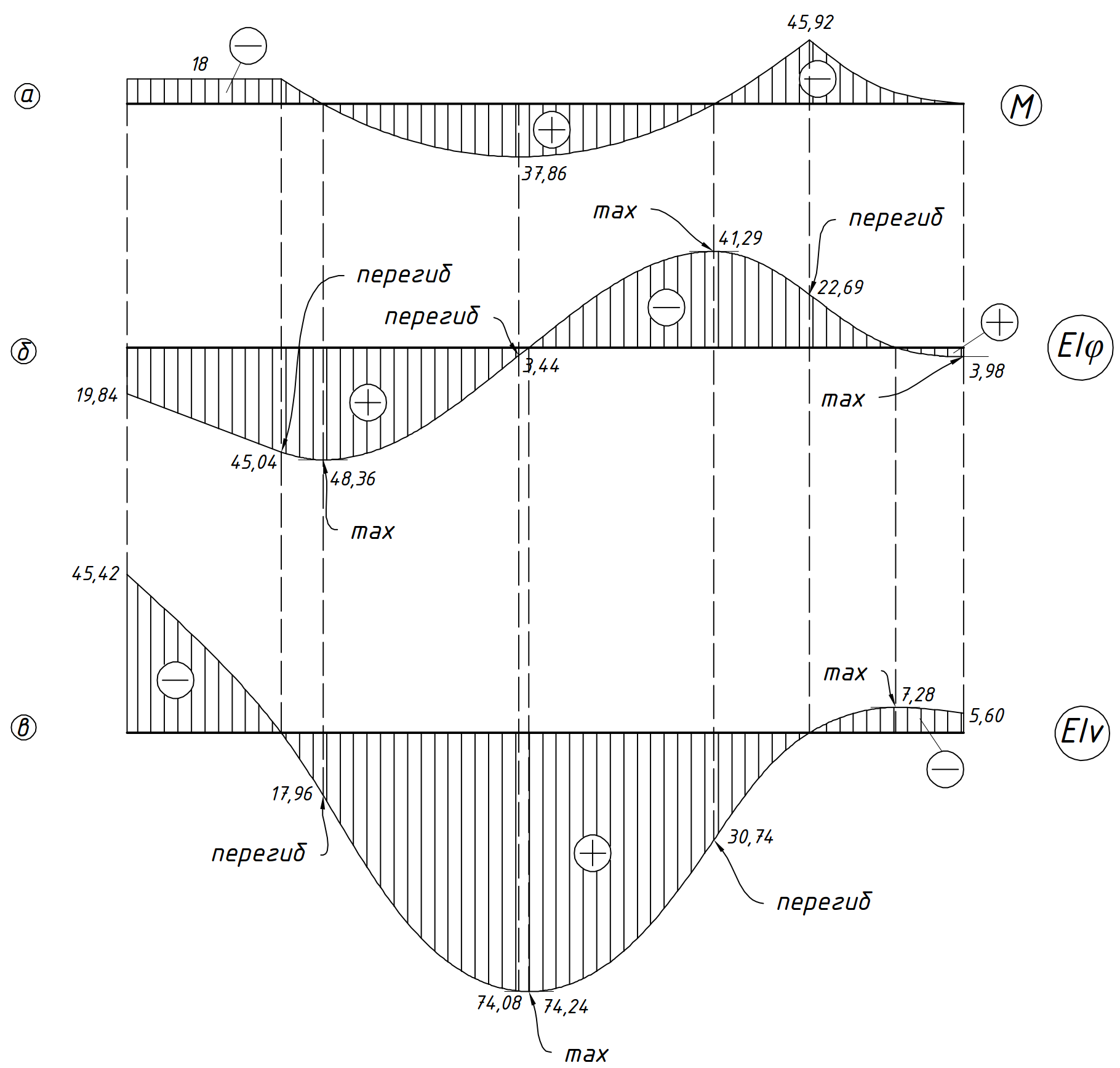 Рисунок 1.5 7. Найдём максимальные значения 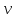 и и 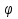 . .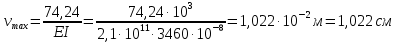 ; ;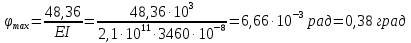 |

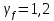 , коэффициент условий работы
, коэффициент условий работы 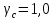 , расчётное сопротивление стали по пределу текучести
, расчётное сопротивление стали по пределу текучести 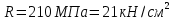 ;
; 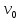 и
и 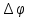 , а также значения
, а также значения 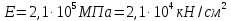 .
. 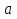 , м
, м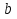 , м
, м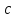 , м
, м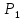 , кН
, кН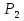 , кН
, кН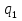 ,
,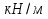
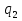 ,
,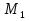 ,
,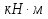
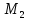 ,
,