01 кр_160502_Костюченко. Задача Определить давление внутри капли воды диаметром, которое создают силы поверхностного натяжения. Температура воды

• Название: Задача Определить давление внутри капли воды диаметром, которое создают силы поверхностного натяжения. Температура воды
• Дата: 04.04.2021
• Размер: 224 Kb.
• Имя файла: 01 кр_160502_Костюченко.doc
• Тип: Решение; #191131

1 Плотность жидкостей. Сжимаемость и температурное расширение жидкостей. Вязкость жидкостей
Задача 1. Определить давление внутри капли воды диаметром , которое создают силы поверхностного натяжения. Температура воды .
Решение
Давление внутри капли воды определяем по формуле Лапласа для криволинейных поверхностей:

(1)

где - поверхностное натяжение воды, соприкасающейся с воздухом, при нормальных физических условиях;

- радиус капли, ;



Ответ: .
2 Основное уравнение гидростатики
Задача 2. Сосуд, имеющий форму конуса с диаметром основания D, переходит в цилиндр диаметром d (рис. 2.3). В цилиндре перемещается поршень с нагрузкой G=3000 Н. Размеры сосуда: D=1 м; d=0,5 м; h=2 м; плотность жидкости ρ=1000 кг/м³. Определить усилие, развиваемое на основание сосуда.



Рисунок 2.3
Решение
Давление на дне сосуда определяется по формуле:

(1)

где - ускорение свободного падения (справочная величина), .

В рассматриваемом случае давление на поверхности жидкости в сосуде составляет:

(2)

где - площадь поперечного сечения цилиндра диаметром , ;

(3)

Подставляя выражение (3) в выражение (2), получаем:

(4)


Подставляя полученное значение в формулу (1), находим: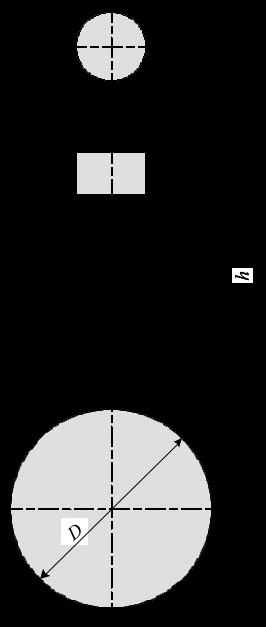





Рисунок 2.3.1

Определяем усилие, развиваемое на основание сосуда:

(5)

где - площадь поперечного сечения основания сосуда, ;

(6)
Подставляя выражение (6) в выражение (5), получаем:

(7)


Ответ: Р=27,4 кН.
3 Сила давления жидкости на стенку (плоскую и криволинейную)
Задача 3. Определить силу давления на основание резервуара (рис. 2), а также силу, действующую на землю под резервуаром, если h3 м; b3 м; ρ10³кг/м³; l₁6 м; α60°; g9,8 м/с². Объяснить полученные результаты. Весом резервуара можно пренебречь.


Рисунок 2
Решение
Сила давления на основание резервуара равна весу воды в объеме :

(1)

где - плотность жидкости в резервуаре, ;

- ускорение свободного падения (справочная величина), ;

- объем усеченной пирамиды, ;

(2)
тут - верхний размер стороны пирамиды, ;

(3)


тогда


Подставляя полученное значение в выражение (1), находим:


Сила, действующая на землю под резервуаром, определяется по основному уравнению гидростатики:

(4)


Сравнивая и видим, что . Это свойство жидкости, на первый взгляд противоречащее обычным представлениям, в чем и заключается гидравлический парадокс.
Ответ: G684, 25 кН, P_f530 кН.
4 Уравнение неразрывности. Уравнение Бернулли
Задача 4. Идеальная жидкость относительной плотностью δ0,8 перетекает через систему трех трубопроводов с диаметрами d₁50 мм, d₂70 мм, d₃40 мм под постоянным напором Н16 м (рис. 3). Трубопроводы полностью заполнены жидкостью. Определить расход жидкости Q.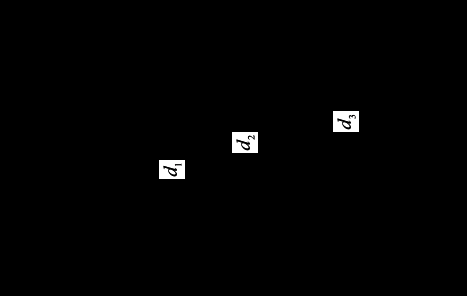


Рисунок 3
Решение
Так как жидкость идеальна, потерями напора можно пренебречь.

Составляем уравнение Бернулли для сечений 0-0 и 3-3, относительно плоскости сравнения 5-5 (рис. 3.1):

(1)

где , , , , так как скорость .

После подстановки всех параметров уравнение Бернулли принимает вид

(2)

откуда

(3)
Расход жидкости:

(4)

где - площадь живого сечения трубопровода диаметром , ;

(5)

Подставляя выражения (3) и (5) в выражение (4), получаем: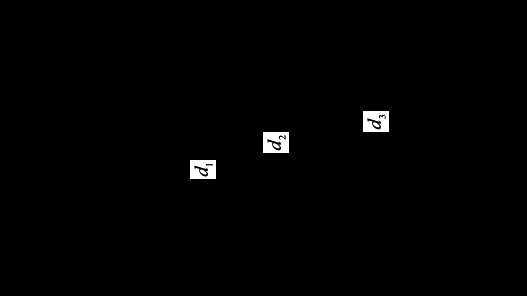

(6)




Рисунок 3.1
Для проведения пьезометрической линии рассчитаем скоростной и пьезометрический напоры.

(7)



(8)



(9)



(10)


Сложив напоры, убедимся в правильности решения, то есть:


Ответ: Q22,2 л/с.
5 Режим течения жидкости в трубах. Гидравлические потери
Задача 5.1 Горизонтальный отстойник для осветления сточных вод представляет собой прямоугольный резервуар шириной b6,0 м и глубиной h2,5 м. Температура воды 20°С. Определить среднюю скорость и режим движения сточной жидкости, если ее расчетный расход Q0,08 м³/с При какой скорости движения жидкости в отстойнике будет наблюдаться ламинарный режим движения жидкости?
Решение
Скорость движения воды в отстойнике:

(1)

где - площадь живого сечения отстойника, ;

(2)

Подставляя выражение (2) в выражение (1), получаем:

(3)


Гидравлический радиус отстойника:

(4)

где - смоченный периметр, ;

(5)


тогда



Число Рейнольдса:

(6)

где - коэффициент кинематической вязкости воды при (справочная величина), ;



Так как полученное значение числа Рейнольдса больше критического значения для открытых русел 500÷600, то режим течения жидкости в отстойнике турбулентный.
Режим течения жидкости в отстойнике турбулентный. Критическую скорость, при которой движение жидкости переходит от ламинарного к турбулентному определяем из выражения:

(7)

откуда

(8)



В отстойниках расчетная скорость принимается равной 5÷10 мм/с, то есть движение жидкости всегда является турбулентным.
Ответ: υ5,3 мм/с, режим движения турбулентный, ламинарный режим движения жидкости будет наблюдаться при υ≤5,3 мм/с.

Задача 5.2 Определить скорость, соответствующую переходу ламинарного режима движения жидкости в турбулентный, если диаметр трубопровода d100 мм, кинематический коэффициент вязкости жидкости ν1,01∙10^-6 м²/с.
Решение
Критическую скорость, при которой движение жидкости переходит от ламинарного к турбулентному определяем из выражения:

(1)
откуда

(2)
где - число Рейнольдса при котором происходит смена режимов течения жидкости;


следовательно, при режим течения жидкости ламинарный, при - турбулентный.
Ответ: υ_кр0,0234 м/с.
Библиографический список
1 Лойцянский, Л.Г. Механика жидкости и газа:Учеб.пособие для ун-тов и втузов [Текст] / Л.Г.Лойцянский – М.: Физматгиз, 1959. - 784 с.

2 Рабинович, Е.З. Гидравлика [Текст] /Е.З. Рабинович – М.: Недра, 1974. - 295 с.

3 Гукасов, Н.А.Механика жидкости и газа: Учеб.для вузов[Текст] /Н.А.Гукасов – М.: Недра, 1996. - 443 с.

4 Арустамова, Ц. Т. Гидравлика: учеб.пособие для вузов[Текст] /Ц. Т.Арустамова,В. Г. Иванников – М.: Недра, 1995. - 198 с.

5 Кудинов, В.А.Гидравлика: Учеб.пособие для вузов по специальностям в обл. техники и технологии [Текст] /В. А. Кудинов, Э. М. Карташов. - М.: Высш. шк., 2006. - 175 с.

6 Штеренлихт, Д.В.Гидравлика: Учеб.для вузов по направлениям в обл. техники и технологии, сел. и рыб. хоз-ва[Текст] / Д. В. Штеренлихт – М.: Колос, 2006. - 656 с.