Задача 1 Вар 7 итог. Задача Определить величину и направление реакций связей для схемы

• Название: Задача Определить величину и направление реакций связей для схемы
• Дата: 30.05.2022
• Размер: 6.76 Mb.
• Имя файла: Задача 1 Вар 7 итог.docx
• Тип: Задача; #557514

Задача 1.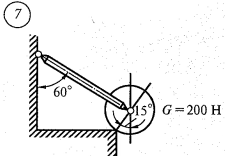



Определить величину и направление реакций свя­зей для схемы.

Решение.



1. В задаче рассматривается равновесие тела, опи­рающегося на плоскость и подвешенного на стерржень. Заменим тело точкой 0, совпадающей с центром тяжести.
2. Приложим к точке 0 активную силу, которой является соб­ственный вес тела G. Направим ее вниз.
3. Мысленно отбросим связи — плоскость и стержень. Заменим их действие на точку 0 реакциями связей. Реакция плоскости (обо­значим ее R) проходит по нормали к плоскости в точке А, а ре­акция или усилие в стержне (обозначим ее S) — по стержню от точки. Обе реакции и вес тела или линии их действия должны пересе­каться в точке 0.
4. Выберем положение системы координат. Начало координат совмещаем с точкой 0. Ось х совмещаем с направлением линии действия реакции R, а ось у направим перпендикулярно оси х. Определим углы между осями координат и реакциями R и S. 
5. Составим сумму проекций всех сил на оси координат:

1) ∑X = R + S∙sin15 – G∙cos15 = 0

1) ∑Y = S∙cos15 – G∙sin15 = 0

Решим систему уравнений. Из второго уравнения находим

S = G∙sin15 / cos15 = 200∙0,259 / 0,966 = 53,6 Н
Из первого уравнения находим

R = - S∙sin15 + G∙cos15 = - 53,6∙0,259 + 200∙0,966 = 179,3 Н

Ответ: R=179,3 Н; S = 53,6 Н.

Задача 2.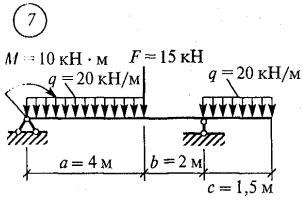



Определить опорные реакции балки на двух опорах по данным своего варианта. Проверить правильность их определения.
Решение.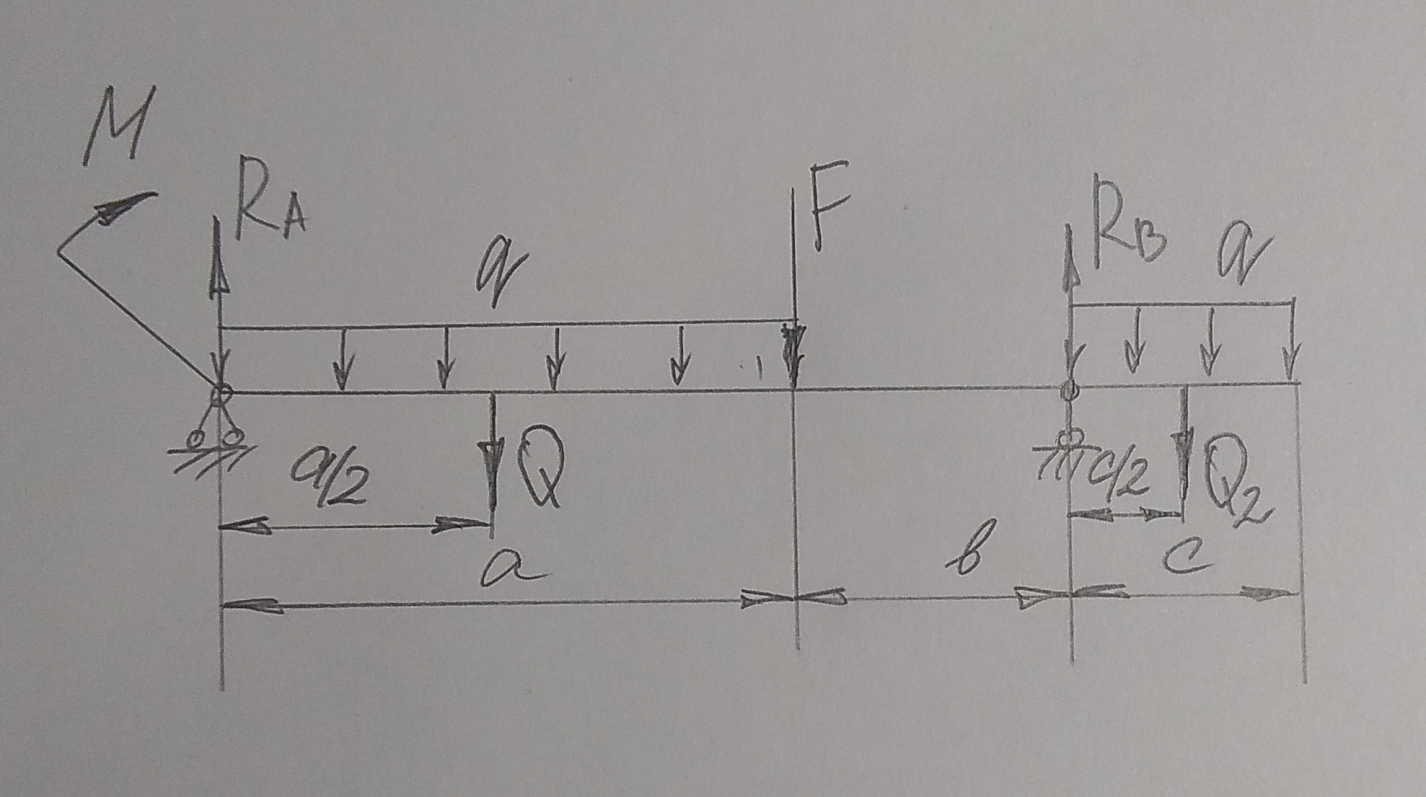

1.Выразим распределенные нагрузки q через сосредоточенные силы

Q₁ = q∙ a = 20 ∙ 4 = 80 кН

Q₂ = q∙ c = 20 ∙ 1,5 = 30 кН

2.Составим уравнения равновесия и решим их

∑M_A (F_i) = 0.

R_B ∙ (a+b) - F∙a – Q₁ ∙ a/2 - Q₂ ∙ (a+b+c/2) - М = 0
R_B = (F∙a + Q₁ ∙ a/2 + Q₂ ∙ (a+b+c/2) + М) / (a+b) = (15∙4 + 80∙2 + 30 ∙ (4+2+1,5/2) + 10) / 6 = 72,083 кН
∑M_B (F_i) = 0.

-R_A ∙ (a+b) + F∙b + Q₁ ∙ (b+a/2) - Q₂ ∙ c/2 - М = 0
R_A = (F∙b + Q₁ ∙ (b+a/2) - Q₂ ∙ c/2 - М) / (a+b) = (15∙2 + 80∙4 - 30 ∙ 1,5/2 - 10) / 6 = 52,917 кН
3.Проверка правильности определения

∑X = R_A + R_B - F - Q₁ - Q₂ = 0

52,917 + 72,083 – 15 – 80 – 30 = 0

125 – 125 = 0.
Реакции определены верно


Задача 3.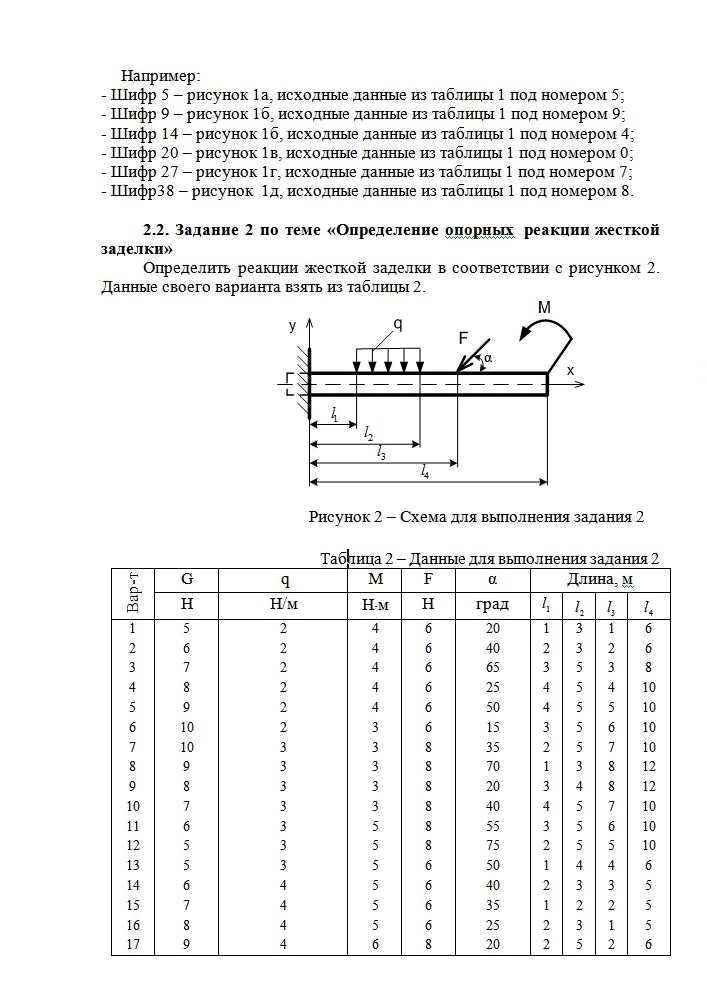

Вариант	G	q	M	F	α	Длина, м
	Н	Н/м	Н·м	Н	град	l1	l2	l3	l4
7	10	3	3	8	35	2	5	7	10

Определить реакции жёсткой заделки.
Решение.

1.Выразим распределенную нагрузки q через сосредоточенную силу

Q = q∙ (l₂-l₁) = 3 ∙ (5-2) = 9 Н

2.Составим уравнения равновесия и решим их

∑M_A (F_i) = 0.

М_A - F∙l₃ ∙ sin α – Q ∙ (l₂+l₁) /2 – G ∙ l₄/2+ М = 0
М_A = F∙l₃ ∙ sin α + Q ∙ (l₂+l₁) /2 + G ∙ l₄/2 - М = 8∙7∙ sin 35 + 9∙(2+5)/2 + 10∙10/2– 3 = 98,57 Н
∑Y = 0.

R_A - F∙sin α - Q - G = 0,
R_A = F∙sin α + Q + G = 8∙ sin 35 + 9 + 10 = 23,59 Н.
∑X = 0.

H_A - F∙cos α = 0,
H_A = F∙cos α = 8∙cos 35 = 6,55 Н.