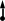Задача на сжатие. Задача 1.Растяжение-сжатие. Задача Осевая деформация растяжениясжатия стержней

• Название: Задача Осевая деформация растяжениясжатия стержней
• Анкор: Задача на сжатие
• Дата: 15.02.2022
• Размер: 0.51 Mb.
• Имя файла: Задача 1.Растяжение-сжатие.docx
• Тип: Задача; #362568

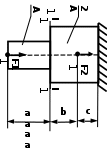
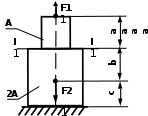
Задача 1. Осевая деформация растяжения-сжатия стержней

с учетом собственного веса
Для стального бруса по заданной схеме (рис. 1 – 3) с учетом собственного веса и при продольных нагрузках F₁, F₂, F₃ (табл. 1), (принять F₃= 2 F₁) требуется:

1. 
   Построить эпюры: продольных сил N_x, нормальных напряжений σ_x и перемещений U_x.
   
2. 
   Вычислить полное удлинение (укорочение) бруса и перемещение сечения I-I для заданных геометрических размеров, заданной схемы, где γ = 77 кН/м³ - удельный вес материала.
   

Варианты заданий даны на рис. 1 – 2. Исходные данные приведены в табл. 1.

Варианты № 1, 11, 21	Варианты № 2, 12, 22

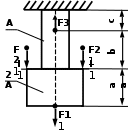
Рис. 1. Задание 1. Осевая деформация растяжения-сжатия стержней

с учетом собственного веса.

Варианты задания 1-2, 11 – 12, 21 – 22

Продолжение вариантов задания 1

Варианты № 3, 13, 23	Варианты № 4, 14, 24

Вариант № 5, 15, 25	Вариант № 6, 16, 26

Варианты № 7, 17, 27	Варианты № 8, 18, 28

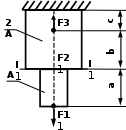
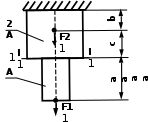
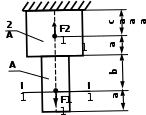
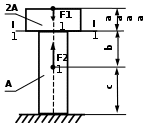
Рис. 2. Задание 1. Осевая деформация растяжения-сжатия стержней

с учетом собственного веса.

Варианты задания 3-8, 13 – 18, 23 – 28

Окончание вариантов задания 1

Варианты 9, 19, 29	Варианты 10, 20, 30

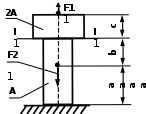
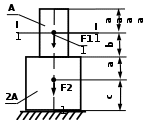
Рис. 3. Задание 1. Осевая деформация растяжения-сжатия стержней

с учетом собственного веса.

Варианты задания 9-10, 19 – 20, 29 – 30
Таблица 1

Исходные данные задания 1. Деформация растяжения – сжатия

Номер Варианта задания	a, м	b, м	c, м	A, см2	F1, кН	F2, кН
1	2,0	1,0	1,5	50	30	17
2	1,5	1,7	2,0	10	32	45
3	1,2	2,3	2,0	12	34	55
4	1,0	2,5	1,6	60	36	10
5	2,0	3,0	2,2	20	40	35
6	1,0	2,5	1,6	25	22	70
7	1,1	2,2	3,0	30	20	26
8	1,2	2,3	1,4	35	18	38
9	1,4	2,1	1,6	40	16	90
10	1,5	1,0	1,8	45	12	54
11	1,6	1,1	2,0	14	10	25
12	1,0	1,2	2,2	36	25	10
13	2,5	1,8	2,4	38	32	55
14	2,4	2,0	1,0	22	36	42
15	2,2	2,4	1,4	24	42	12
16	2,1	2,2	3,5	26	52	75

Номер Варианта задания	a, м	b, м	c, м	A, см2	F1, кН	F2, кН
17	1,0	2,1	3,0	30	40	65
18	1,0	3,5	2,2	28	55	10
19	1,8	3,0	1,4	32	65	18
20	1,5	1,1	2,0	45	60	22
21	1,5	1,0	1,8	44	50	10
22	2,0	1,8	1,0	25	22	58
23	1,6	2,0	1,6	45	30	33
24	1,4	2,5	3,0	55	45	16
25	1,0	2,2	1,4	16	48	50
26	1,3	2,2	3,0	22	50	14
27	1,5	1,8	2,4	40	60	22
28	2,0	1,5	1,0	36	35	40
29	2,5	2,0	1,8	48	14	30
30	2,2	3,0	2,5	15	27	45

Окончание табл. 1
Пример выполнения задания 1. Деформация растяжения-сжатия стержня с учетом собственного веса.

Стальной стержень (Е=2 · 10⁵ МПа) находится под действием продольной силы F и собственного веса (γ = 77 кН/м³- удельный вес материала). Построить эпюру продольных усилий N_x, эпюру нормальных напряжений σ_х, эпюру перемещений U_x. Вычислить перемещение сечения δ_I-I.

Дано: А = 60 см² = 6010^-4 м², а = 1,0 м, в = 1,5 м, с = 2,5 м, F = 40 кН

Решение

1. 
   Условно разделим стальной стержень на 3 участка (рис.1), вычислим вес каждого участка: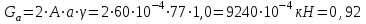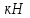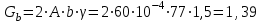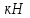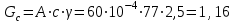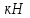
   

Ϭ_х, МПа

43,47

7,25


U_х10^-4, м

N_х, кН

O

6

6
0,


+

+

c


v

v

G_c




3,53

0,894

I

I

5

5




7,06

42,31

D

4

4
,

+

v

G_b

v

+

v

+

b





3,41

1,154

40,92

3

3




0,077

0,92

2

2

B

F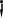



G_a

a

0


1,155

K

1

1
1




Рис. 1. Пример построения эпюр продольных сил N_x,

нормальных напряжений σ_х, осевых перемещений U_x
2. Проверим целесообразность учёта собственного веса в данной задаче.

Суммарный вес стержня: .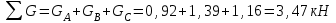

Заданная нагрузка F=40 кН. Вычислим процент, который составит суммарный вес стержня к заданной величине силы: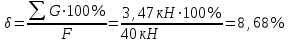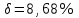



> [5%], следовательно, собственный вес стержня учитывать необходимо.

3. Вычислим продольные усилия N_x, нормальные напряжения σ_х и построим эпюры «N_x», «σ_х» в выбранном масштабе, (+) – деформация растяжения, (–) – деформация сжатия.

Участок 1-2: ;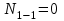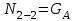

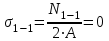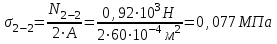	N	σ
1 – 1	0	0
2 – 2	0,92	0,077

Участок 3-4: ;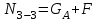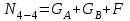

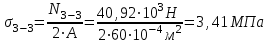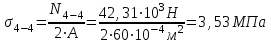	N	σ
3 – 3	40,92	3,41
4 – 4	42,31	3,53

Участок 5-6: ;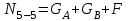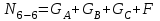

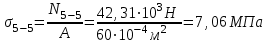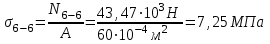	N	σ
5 – 5	42,31	7,06
6 – 6	43,47	7,25

По полученным данным строим эпюры в выбранном масштабе, в данном случае все участки растянуты, следовательно, произошла деформация растяжения (+).

4. Вычислим перемещение сечения I-I: 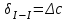; – равно сумме перемещений деформаций участков. Используем развернутый Закон Гука для определения деформации (удлинения) каждого участка: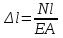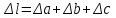

,

.

где ;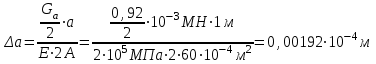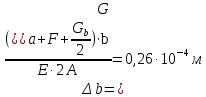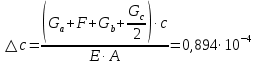

;



тогда: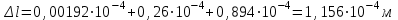



Для построения эпюры перемещений U_x, рассмотрим перемещение поперечного сечения стержня в характерных точках: О, В, С, К.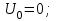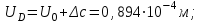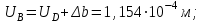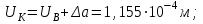









Перемещение сечения I-I: 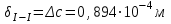– происходит за счёт растяжения верхнего участка «с».

При заданной схеме происходит удлинение стержня на длину 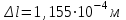.