Отчет. ОТЧЕТ. Задача По результатам корреляционного анализа (см задание 1) выбрать пару факторов, которые связаны наиболее тесно, обозначив их x и y соответственно.

• Название: Задача По результатам корреляционного анализа (см задание 1) выбрать пару факторов, которые связаны наиболее тесно, обозначив их x и y соответственно.
• Анкор: Отчет
• Дата: 07.05.2022
• Размер: 88.55 Kb.
• Имя файла: ОТЧЕТ.docx
• Тип: Задача; #516472
• страница: 2 из 2

Выводы:

1. 
   , следовательно, основная гипотеза отвергается, т.е параметр статистически значим. Если параметр является значимым, то соответствующая ему интерпретация не противоречит изучаемому процессу, т.е. если количество посетителей в среднем увеличивается, то выручка от продажи томатов в среднем увеличивается.
   

В нашем случае, гипотеза отвергается.

2. 
   , следовательно, основная гипотеза отвергается, т.е параметр статистически значим. Если параметр является значимым, то соответствующая ему интерпретация не противоречит изучаемому процессу, т.е. что изменение средней выручки от продажи томатов происходит медленнее изменения среднего количества посетителей.
   

В нашем случае гипотеза так же отвергается. Значит наши параметры статистически значимы.

Построим доверительные интервалы для параметров.

₀ = (5,844; 14,348)

₁ = (0,040; 0,048)

Выводы:

Интерпретация значения θ₀ напрямую отсутствует, доверительный интервал показывает, в каких границах он варьируется.

Доверительный интервал для θ₁ показывает, сколько в среднем один посетитель покупает томатов на сумму от 40 до 48 руб. Следовательно, предположение из уравнения прямой регрессии о том, что в среднем один покупатель приобретает томатов на 44 рублей соответствует доверительному интервалу.

Задание 4

Таблица 7 – Вспомогательная таблица

TSS (Общая сумма квадратов)	24817,395
ESS (Остаточная сумма квадратов)	1929,826
RSS (Объясненная сумма квадратов)	22887,569
R2 (коэффициент детерминации)	0,922
F (F-статистика)	569,276
Fкр	4,043

На практике истинное значение , как правило, неизвестно. Поэтому для оценки качества уравнения регрессии используется его выборочный аналог, вычисляемый по формуле:

0,922

Данная величина показывает долю объясненной дисперсии в общей дисперсии зависимой переменной.

Гипотезы:





Вывод: Так как F > F крит, то гипотеза отвергается, коэффициент детерминации признается значимым, следовательно, модель признается значимой и ее можно использовать для прогнозирования.

Задание 5

Таблица 7 – Дисперсионный анализ

Источник дисперсии	Число степеней свободы	Сумма квадратов	На одну степень свободы	F	Fкр	Значимость
Объясняющая (х)	1	22887,569	1250,593	569,276	4,043	Да
Остаточная	48	1929,826	409,313	-	-	-
Общая	49	24817,395	426,482	-	-	-

Вывод: В эту таблицу включены все основные результаты расчетов, проводимых при проверке значимости регрессионной модели, а именно TSS , RSS и ESS – элементы из разложения TSS=ESS+RSS ; F  статистика Фишера, вычисляемая по формуле F= ; Fкр – критическое значение статистики Фишера для соответствующего уровня доверительной вероятности.

Исходя из расчетов можно сделать вывод что регрессионная модель значима, и ее можно использовать для прогнозирования.

Задание 6

Таблица 8 - Точечный и интервальный прогноз

X прогнозное	2220
S (Оценка СКО ошибок)	6,341
∑(Xi-Xср)^2	11784203,220
σ (sigma) y^п оценка СКО ошибки прогноза	2,653
у^п оценка отклика/прогноз	107,933

Выберем прогнозную точку , определим, сколько будет выручки от продаж томатов при 2220 человек.

Точечный прогноз:





Это значит, что при 2220 человек в магазине, выручка от продажи томатов будет составлять тыс. руб.

Интервальный прогноз:



t кр (0,05; 48) = 2,3139

Интервал для : [101,794; 114,071]

Вывод:

Точечный прогноз ожидаемое значение зависимой переменной, показало, что выручка от продажи томатов будет составлять тыс. руб.

Интервальное прогнозирование интервал, в котором с известной доверительной вероятностью находится истинное значение зависимой переменной показало, что при 2220 посетителей, выручка от продажи томатов составит [101,794; 114,071] тыс. руб.

Задание 7

Изменение доверительной вероятности оказывает существенное влияние и на интервальный прогноз. Так, при увеличении доверительной вероятности ширина доверительного интервала должна расти, а при уменьшении – сокращаться.

Рассчитываем ошибку прогноза по формуле: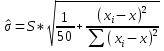



Таблица 9 – Доверительный интервал и ошибка прогноза на всем диапазоне данных

X	Y^	σ(sigma) у^п (ошибка прогноза)	Нижняя граница	Верхняя граница
2108	102,997	1,674	99,123	106,870
1726	86,162	1,700	82,227	90,096
1758	87,572	1,698	83,642	91,501
1514	76,819	1,715	72,850	80,787
2103	102,776	1,674	98,902	106,651
1371	70,517	1,725	66,525	74,508
1332	68,798	1,728	64,800	72,796
1039	55,885	1,748	51,840	59,930
972	52,932	1,753	48,876	56,988
1361	70,076	1,726	66,083	74,069
1388	71,266	1,724	67,277	75,255
1334	68,886	1,728	64,888	72,883
876	48,702	1,760	44,630	52,773
1172	61,747	1,739	57,723	65,770
1011	54,651	1,750	50,601	58,701
900	49,759	1,758	45,692	53,827
1166	61,482	1,739	57,457	65,507
1049	56,326	1,747	52,282	60,369
818	46,145	1,764	42,065	50,226
934	51,258	1,756	47,196	55,320
955	52,183	1,754	48,124	56,242
958	52,315	1,754	48,257	56,374
1206	63,245	1,737	59,227	67,263
774	44,206	1,767	40,118	48,294
940	51,522	1,755	47,461	55,583
1011	54,651	1,750	50,601	58,701
936	51,346	1,755	47,284	55,408
1174	61,835	1,739	57,811	65,858
1093	58,265	1,744	54,229	62,301
912	50,288	1,757	46,222	54,354
480	31,250	1,787	27,114	35,385
490	31,690	1,787	27,556	35,825
474	30,985	1,788	26,848	35,122
262	21,642	1,803	17,471	25,814
345	25,300	1,797	21,142	29,458
299	23,273	1,800	19,107	27,438
354	25,697	1,796	21,540	29,853
334	24,815	1,798	20,656	28,975
352	25,609	1,796	21,452	29,765
470	30,809	1,788	26,671	34,946
487	31,558	1,787	27,423	35,693
307	23,625	1,800	19,461	27,789
327	24,507	1,798	20,346	28,668
328	24,551	1,798	20,390	28,711
251	21,157	1,804	16,984	25,331
498	32,043	1,786	27,910	36,176
284	22,612	1,801	18,444	26,780
453	30,060	1,789	25,919	34,200
288	22,788	1,801	18,621	26,955
443	29,619	1,790	25,477	33,761

Построим график: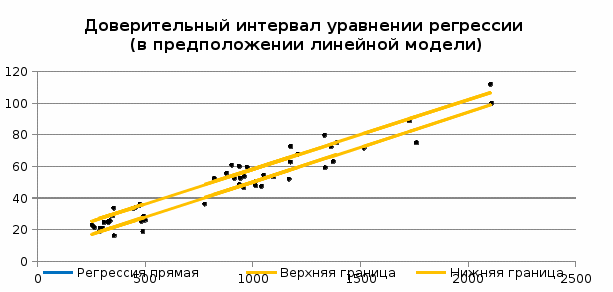



Рисунок 2 - Корреляционное поле, линия регрессии, 95% доверительный интервал

Справедливость структуры модели становится под сомнение, так как 20 точек на графике наблюдений не попадают в доверительный интервал. Оценка стандартной ошибки прогнозирования должна быть рассчитана по другой формуле. Необходимо увеличить доверительный интервал.

Рассчитываем ошибку прогноза по формуле: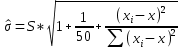



Таблица 10 - Доверительный интервал и ошибка прогноза на всем диапазоне данных

X	Y^	σ(sigma)y^п оценка СКО ошибка прогноза 2	Нижняя граница 2	Верхняя граница 2
2108	102,997	6,558	87,822	118,171
1726	86,162	6,565	70,971	101,352
1758	87,572	6,564	72,383	102,761
1514	76,819	6,569	61,620	92,018
2103	102,776	6,558	87,602	117,951
1371	70,517	6,571	55,312	85,722
1332	68,798	6,572	53,591	84,005
1039	55,885	6,577	40,666	71,104
972	52,932	6,579	37,710	68,154
1361	70,076	6,571	54,870	85,281
1388	71,266	6,571	56,061	86,470
1334	68,886	6,572	53,679	84,093
876	48,702	6,580	33,475	63,928
1172	61,747	6,575	46,533	76,960
1011	54,651	6,578	39,431	69,872
900	49,759	6,580	34,534	64,984
1166	61,482	6,575	46,268	76,696
1049	56,326	6,577	41,107	71,545
818	46,145	6,581	30,917	61,374
934	51,258	6,579	36,034	66,481
955	52,183	6,579	36,960	67,406
958	52,315	6,579	37,093	67,538
1206	63,245	6,574	48,033	78,457
774	44,206	6,582	28,976	59,437
940	51,522	6,579	36,299	66,746
1011	54,651	6,578	39,431	69,872
936	51,346	6,579	36,122	66,569
1174	61,835	6,575	46,621	77,048
1093	58,265	6,576	43,048	73,482
912	50,288	6,580	35,063	65,513
480	31,250	6,588	16,006	46,493
490	31,690	6,588	16,447	46,933
474	30,985	6,588	15,741	46,229
262	21,642	6,592	6,389	36,895
345	25,300	6,590	10,050	40,550
299	23,273	6,591	8,021	38,524
354	25,697	6,590	10,448	40,946
334	24,815	6,591	9,565	40,065
352	25,609	6,590	10,359	40,858
470	30,809	6,588	15,565	46,053
487	31,558	6,588	16,315	46,801
307	23,625	6,591	8,374	38,877
327	24,507	6,591	9,256	39,757
328	24,551	6,591	9,301	39,801
251	21,157	6,592	5,904	36,411
498	32,043	6,587	16,800	47,286
284	22,612	6,592	7,359	37,864
453	30,060	6,588	14,815	45,304
288	22,788	6,592	7,536	38,040
443	29,619	6,589	14,374	44,864

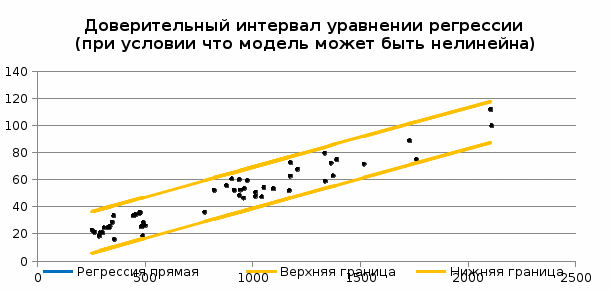Рисунок 3 - Корреляционное поле, линия регрессии, 95% доверительный интервал

Справедливость структуры модели не становится под сомнение, так как 95% наблюдений попадают в доверительный интервал. Таким образом, с вероятностью 95% при прогнозируемом количестве посетителей в 2220 человек, выручка от продажи томатов будет находится в пределах найдено доверительного интервала.

Задание 8

Используя данные корреляционного анализа, выявили наиболее тесную связь факторов. Ей стала связь между количеством посетителей и выручкой от продажи томатов. Далее по методу наименьших квадратов вычислили оценки неизвестных параметров для уравнений парной регрессии. Дали интерпретацию результатов и выбрали для дальнейшего анализа одно из уравнений. Записали и оценили уравнение ортогональной регрессии. Построили и проанализировали графическую интерпретацию всех трех моделей регрессии и исходных данных. Проверили на значимость всех параметров выбранной модели регрессии по критерию Стьюдента. Для значимых коэффициентов построили доверительные интервалы. Проверили значимость модели (уравнения регрессии) в целом с помощью критерия Фишера. Построили таблицу дисперсионного анализа. Выбрали прогнозную точку x_П в стороне от основного массива данных. Выполнили точечный и интервальный прогнозы величины y в точке х_П.. Построили 95% доверительный интервал для уравнения регрессии на всем диапазоне исходных данных. Изобразили в одной системе координат исходные данные, линию регрессии, 95% доверительный интервал, проанализировали полученный график.

Рекомендации:

1. 
   Доверительный интервал для θ₁ показывает, сколько в среднем один посетитель покупает томатов на сумму от 40 до 48 руб. Следовательно, предположение из уравнения прямой регрессии о том, что в среднем один покупатель приобретает томатов на 44 рублей соответствует доверительному интервалу.
   
2. 
   Если выручка от продажи томатов будет увеличиваться на 1 тыс. руб., то возможно среднее количество посетителей изменится в большую сторону на 20 людей.
   
3. 
   Интервальное прогнозирование показало, что при 2220 посетителей, выручка от продажи томатов составит [101,794; 114,071] тыс. руб.