Отчет. ОТЧЕТ. Задача По результатам корреляционного анализа (см задание 1) выбрать пару факторов, которые связаны наиболее тесно, обозначив их x и y соответственно.

Название	Задача По результатам корреляционного анализа (см задание 1) выбрать пару факторов, которые связаны наиболее тесно, обозначив их x и y соответственно.
Анкор	Отчет
Дата	07.05.2022
Размер	88.55 Kb.
Формат файла
Имя файла	ОТЧЕТ.docx
Тип	Задача #516472
страница	1 из 2

1 2

Цель: Ознакомиться с основными положениями, понятиями и методами анализа линейной модели парной регрессии.

Задача: По результатам корреляционного анализа (см. задание №1) выбрать пару факторов, которые связаны наиболее тесно, обозначив их x и y соответственно. Полагая, что связь между ними может быть описана линейной функцией, записать уравнения y = f (x) и x = g(y) , определяющие искомую взаимосвязь.

Выбираем из парных коэффициентов (лабораторная работа №1) наиболее тесную связь:

Таблица – 1 Парные коэффициенты

томаты	лапша	мука	крупа
0,960332	0,943096	0,943096	0,943096

Наиболее тесная зависимость – это зависимость между количеством посетителей и выручкой от продаж томатов, потому что значение коэффициента больше значения других коэффициентов.

Таблица 2 – Исходные данные

	Посетители(х) человек	Томаты(у) тыс. руб.	y^
	Посетители(х) человек	Томаты(у) тыс. руб.	y^
1	2108	100,3	102,997
2	1726	89,1	86,162
3	1758	75,2	87,572
4	1514	71,9	76,819
5	2103	112,3	102,776
6	1371	63,2	70,517
7	1332	80	68,798
8	1039	47,7	55,885
9	972	59,8	52,932
10	1361	72,7	70,076
11	1388	75,3	71,266
12	1334	59,4	68,886
13	876	55,9	48,702
14	1172	63,1	61,747
15	1011	48,1	54,651
16	900	61,1	49,759
17	1166	52,3	61,482
18	1049	47,2	56,326
19	818	23,9	46,145
20	934	50,2	51,258
21	955	52,2	52,183
22	958	39,4	52,315
23	1206	48	63,245
24	774	44,7	44,206
25	940	47,3	51,522
26	1011	55,5	54,651
27	936	36,5	51,346
28	1174	56,2	61,835
29	1093	40,3	58,265
30	912	52,6	50,288
31	480	21,9	31,250
32	490	20,1	31,690
33	474	21,6	30,985
34	262	26,3	21,642
35	345	12,4	25,300
36	299	23,4	23,273
37	354	18,3	25,697
38	334	29,6	24,815
39	352	27,8	25,609
40	470	22,3	30,809
41	487	27,7	31,558
42	307	23,7	23,625
43	327	23,1	24,507
44	328	18,4	24,551
45	251	19,2	21,157
46	498	10,1	32,043
47	284	26,7	22,612
48	453	12,2	30,060
49	288	26,4	22,788
50	443	13	29,619

Задание 1

Обозначим:

Х – количество посетителей;

У – выручка от продажи томатов.

Формулы парных регрессий:

Таблица – 3 Вспомогательная таблица

Сумма X	43417
Cумма Y	2418,2
Cуммкв X	49484921
Cуммкв Y	141771,2
Cуммпроиз Y	2619158

С помощью метода наименьших квадратов найдем оценки неизвестных параметров уравнений.

Первая система:

Уравнение прямой регрессии:

Вывод: В среднем один покупатель приобретает томатов на 44 рубля, что меньше среднего 48,364. Это значит, что спрос на томаты различный, потому что покупатели приобретают разное кол-во томатов.

При кол-ве посетителей равному 0, выручка от продажи томатов равна 10,096 тысяч рублей, из чего следует, что в нашем случае такое невозможно, поэтому мы не можем интерпретировать

.
Вторая система:

Уравнение обратной регрессии:

Выводы:

Если выручка от продажи томатов будет увеличиваться на 1 тыс. руб., то возможно среднее количество посетителей изменится в большую сторону на 20 людей. 143 посетителей не стали покупать томаты.

Отношение оценок параметров отрицательное значение, то это позволяет сделать вывод о том, что изменение среднего количества посетителей происходит быстрее изменения средней выручки от продажи томатов.

Мы не можем использовать для прогнозирования уравнение обратной регрессии, так как X-выручка от продажи зависимая величина и на нее влияет количество посетителей.

Для дальнейшего использования мы выбираем уравнение прямой регрессии, потому что согласно уравнению обратной регрессии мы получаем зависимость количества посетителей от выручки продажи томатов, что не соответствуют реальности.

Задание 2

Для нахождения ортогональной регрессии, с помощью инструментов MS EXCEL, найдем вспомогательные данные.

Таблица 4 – Вспомогательная таблица

Rxy	0,960
Sx СКО	490,402
Sу СКО	22,505
S0	21,745
θ1^ для орты	0,044
θ0^ для орты	10,089

Для построения уравнения ортогональной регрессии найдем максимальные и минимальные значения.

Таблица 5 -Максимальные и минимальные значения

Теперь изобразим уравнения прямой, обратной и ортогональной регрессий графически.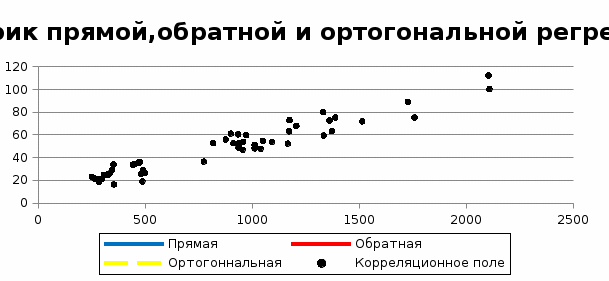

Рисунок 1 – Три модели регрессии

Вывод: Точка пересечения уравнений регрессий, координаты которой соответствуют среднему значению факторов. На графике видно, что ближе к ортогональной регрессии находится прямая регрессия, значит мы выбираем прямую регрессию.

Задание 3

Выдвигаем гипотезы:

Таблица 6 – Вспомогательная таблица
	0,044
	10,096
	1,838
	0,002
	40,205
	5,494
	23,860
	2,314

1 2