Задача по теме Характеристики и модели временных рядов Необходимо выполнить задачу на реальных статистических данных, представляющих практический и теоретический интерес
 Скачать 36.09 Kb. Скачать 36.09 Kb.
|
|
Часть 1. Комплексная задача по теме «Характеристики и модели временных рядов» Необходимо выполнить задачу на реальных статистических данных, представляющих практический и теоретический интерес. Исследуйте динамику экономического показателя на основе анализа одномерного временного ряда. Задания: 1. Постройте график временного ряда, сделайте вывод о наличии и виде тренда. 2. Постройте линейную модель Y(t) = aо + а1 t, оценив ее параметры с помощью метода наименьших квадратов (МНК). 3. Оцените адекватность построенной модели, используя свойства остаточной компоненты e(t). 4. Оцените точность модели на основе средней относительной ошибки аппроксимации. 5. Осуществите прогноз объема продаж на следующие два месяца (доверительный интервал прогноза рассчитайте при доверительной вероятности P = 75%). 6. Фактические значения показателя, результаты моделирования и прогнозирования представьте графически. 7. Используя MS Excel, подберите для данных своего варианта наилучшую трендовую модель и выполните прогнозирование по лучшей модели на два ближайших периода вперед. Представьте в отчете соответствующие распечатки с комментариями о качестве выбранной модели. Продемонстрируйте возможности выполнения пп. 1-6 данной задачи с использованием MS Excel, Gretl. Представьте в отчете соответствующие распечатки с комментариями. Решение: Имеются данные о Среднемесячной номинальной начисленной заработной плате работников Российской Федерации за январь-декабрь 2021 года
Построим график временного ряда 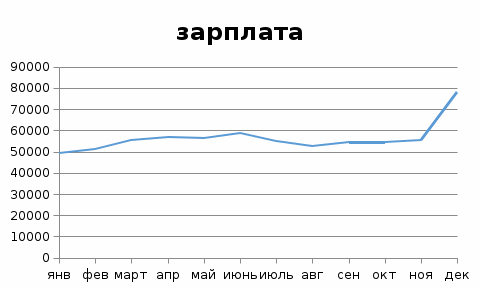 Можно сделать вывод о наличии восходящего тренда. Построим линейную модель 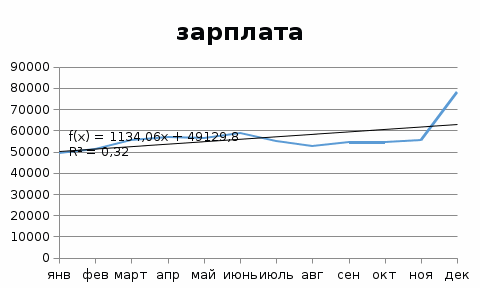 Уравнение линейной регрессии: У = 49130 + 1134,1*t, Где t – номер периода начиная с единицы. Коэффициент детерминации равен 0,3215. т.е. в 32% случаев t влияет на изменение y. Другими словами - точность подбора уравнения тренда - средняя. Оценим качество уравнения тренда с помощью средней относительной ошибки аппроксимации.
Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения тренда к исходным данным. Поскольку ошибка больше 7%, то данное уравнение не рекомендуется использовать в качестве тренда. Интервальный прогноз. Определим среднеквадратическую ошибку прогнозируемого показателя. Uy = yn+L ± K где L - период упреждения; уn+L - точечный прогноз по модели на (n + L)-й момент времени; n - количество наблюдений во временном ряду; Sy - стандартная ошибка прогнозируемого показателя; Tтабл - табличное значение критерия Стьюдента для уровня значимости α и для числа степеней свободы, равного n-2. По таблице Стьюдента находим Tтабл Tтабл (n-m-1;α/2) = (;) = 2.634 Точечный прогноз, t = 13: y(13) = 1134.056*13 + 49129.803 = 63872.53 63872.53 - 19266.6 = 44605.93 ; 63872.53 + 19266.6 = 83139.13 Интервальный прогноз: t = 13: (44605.93;83139.13) Точечный прогноз, t = 14: y(14) = 1134.056*14 + 49129.803 = 65006.59 65006.59 - 19938.9 = 45067.69 ; 65006.59 + 19938.9 = 84945.49 Интервальный прогноз: t = 14: (45067.69;84945.49) Результаты прогнозирования представим графически 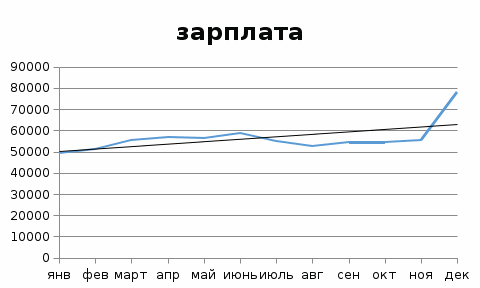 Используя MS Excel, подберем для данных наилучшую трендовую модель. Экспоненциальная модель 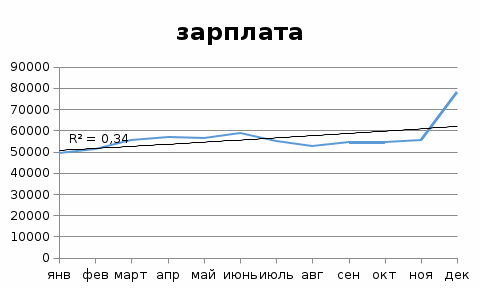 Логарифмическая модель 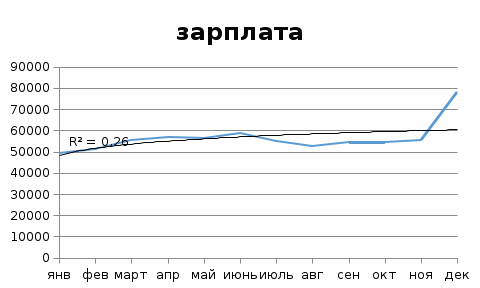 Полиномиальная модель 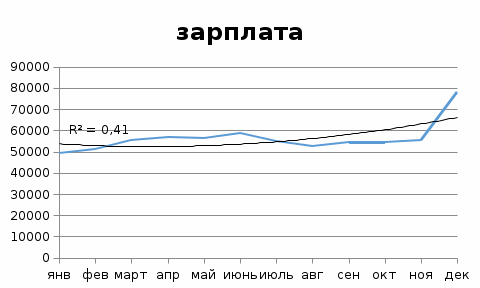 Степенная модель 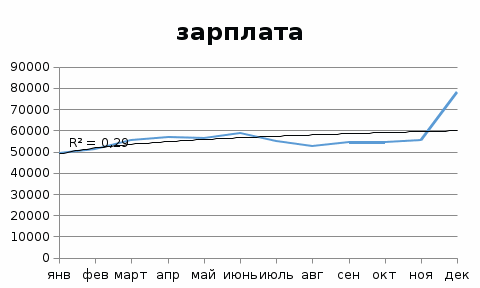 Как видим, наиболее высокий коэффициент детерминации имеет полиномиальная модель. 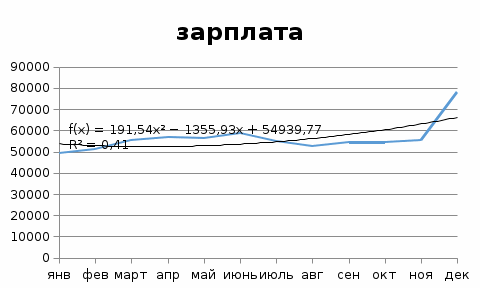 У = 54940 – 13,55,9*t + 191,54*t^2 Результаты прогнозирования
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
