Задания для эконометрики. Задача по теме Характеристики и модели временных рядов Необходимо выполнить задачу на реальных статистических данных, представляющих практический и теоретический интерес
 Скачать 19.2 Kb.
|
|
Часть 1. Комплексная задача по теме «Характеристики и модели временных рядов» Необходимо выполнить задачу на реальных статистических данных, представляющих практический и теоретический интерес. Исследуйте динамику экономического показателя на основе анализа одномерного временного ряда. Задания: 1. Постройте график временного ряда, сделайте вывод о наличии и виде тренда. 2. Постройте линейную модель Y(t) = aо + а1 t, оценив ее параметры с помощью метода наименьших квадратов (МНК). 3. Оцените адекватность построенной модели, используя свойства остаточной компоненты e(t). 4. Оцените точность модели на основе средней относительной ошибки аппроксимации. 5. Осуществите прогноз объема продаж на следующие два месяца (доверительный интервал прогноза рассчитайте при доверительной вероятности P = 75%). 6. Фактические значения показателя, результаты моделирования и прогнозирования представьте графически. 7. Используя MS Excel, подберите для данных своего варианта наилучшую трендовую модель и выполните прогнозирование по лучшей модели на два ближайших периода вперед. Представьте в отчете соответствующие распечатки с комментариями о качестве выбранной модели. Продемонстрируйте возможности выполнения пп. 1-6 данной задачи с использованием MS Excel, Gretl. Представьте в отчете соответствующие распечатки с комментариями. Часть 2. Комплексная задача типа кейс-стади на применение корреляционного, парного и множественного регрессионного анализа данных Необходимо выполнить задачу на реальных статистических данных, представляющих практический и теоретический интерес Задания: Рассчитайте матрицу парных коэффициентов корреляции. Оцените статистическую значимость коэффициентов корреляции Y с каждым из факторов. Проверьте факторы на наличие мультиколлинеарности. Постройте поле корреляции результативного признака Y и наиболее тесно связанного с ним фактора. Рассчитайте параметры парной линейной регрессии для фактора, наиболее связанного с Y. Оцените качество полученной модели через коэффициент детерминации, среднюю ошибку аппроксимации и F-критерий Фишера. Проверьте наличие гетероскедастичности в остатках. При ее наличии оцените модель с корректировкой гетероскедастичности (здесь можно воспользоваться программным продуктом). По модели п. 3 (или 4) осуществите прогнозирование среднего значения показателя Y при уровне значимости 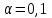 , если прогнозное значение фактора составит 80% от его максимального значения. Представьте на графике фактические, модельные значения и точки прогноза.Постройте нелинейные уравнения парной регрессии (степенную (варианты 1-5), показательную (варианты 6-10), гиперболическую) для фактора, наиболее связанного с Y. Выберите наиболее точную модель. Какая из спецификаций модели лучше: парная линейная или парная нелинейная модель? Ответ обоснуйте. 7. Используя пошаговую множественную регрессию (метод исключения или метод включения), постройте модель формирования результативного признака на основе только статистически значимых факторов ( 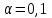). Используя результаты п. 1, постарайтесь не включать в модель коллинеарные факторы. Дайте экономическую интерпретацию коэффициентов модели множественной регрессии.8. Оцените качество построенной модели множественной регрессии. Улучшилось ли качество модели по сравнению с однофакторной моделью? Выполните прогнозирование результативного признака Y по модели множественной регрессии. Сравните результаты прогнозирования по парной и множественной регрессии. 9. Дайте оценку влияния значимых факторов на результат Y с помощью коэффициентов эластичности, 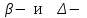 коэффициентов. Определите наиболее влиятельный фактор.Расчеты следует выполнять как вручную, так и с использованием прикладных программных продуктов: Excel, Gretl. Результаты работы с программами включите в отчет по соответствующему заданию. |