Переходные процессы тремя методами. контрольная работа ПП. Задача посвящена анализу переходного процесса в цепи первого порядка, содержащей резисторы, и индуктивность. В момент времени t

• Название: Задача посвящена анализу переходного процесса в цепи первого порядка, содержащей резисторы, и индуктивность. В момент времени t
• Анкор: Переходные процессы тремя методами
• Дата: 08.09.2022
• Размер: 155.96 Kb.
• Имя файла: контрольная работа ПП.docx
• Тип: Задача; #667086

Задача 1

Задача посвящена анализу переходного процесса в цепи первого порядка, содержащей резисторы, и индуктивность. В момент времени t=0 происходит переключение ключа К, в результате чего в цепи возникает переходной процесс.

1. 
   Перерисуйте схему цепи (таблица 2) для Вашего варианта – последним двум цифрам пароля (таблица 1).
   
2. 
   Выпишите числовые данные для Вашего варианта – последним двум цифрам пароля (таблица3).
   
3. 
   Рассчитайте все токи и напряжение на L в три момента времени t: 0_-,0₊,∞
   
4. 
   Рассчитайте классическим методом переходный процесс в видеu_L(t),i₁(t), i₂(t), i₃(t). Проверьте правильность расчетов, выполненных в п. 4, путем сопоставления их с результатами расчетов в п. 3.
   
5. 
   Постройте графики переходных токов и напряжения, рассчитанных в п. 4. Определите длительность переходного процесса, соответствующую переходу цепи в установившееся состояние с погрешностью 5%.
   
6. 
   Рассчитайте ток i₂(t) операторным методом.
   

Исходные данные (вариант 1)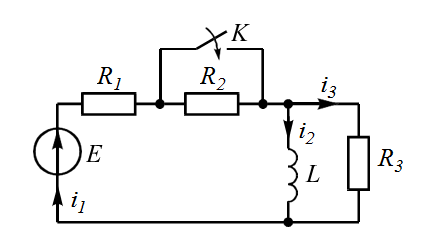



Рис. 1. Схема цепи (2)

L=20 мГн; R₁=2 кОм; R₂=2 кОм; R₃=2 кОм; E=10 В

Решение

1. 
   Рассмотрим переходный процесс в момент времени непосредственно перед коммутацией (t=0_-). Так как до коммутации ключ К разомкнут, а в цепи протекают постоянные токи, то индуктивность можно заменить короткозамкнутым участком. В этом случае схема примет вид, показанный на рис. 2.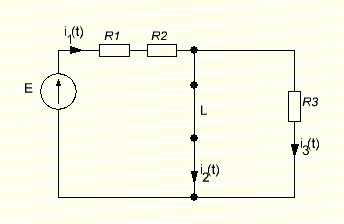
   

Рис. 2. Схема замещения цепи перед коммутацией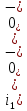



Поскольку сопротивление R₃ замкнуто накоротко индуктивностью, то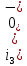



Напряжение на индуктивности перед коммутацией: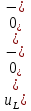



Сразу после замыкания ключа, согласно закону коммутации, ток через индуктивность не может измениться мгновенно, так как для мгновенного изменения запасенной магнитной энергии необходима бесконечно большая мощность, соответственно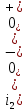



Для расчета двух оставшихся токов запишем систему уравнений Кирхгофа. Поскольку ток i₂(0₊) известен, то достаточно двух уравнений – одного уравнения по первому закону Кирхгофа и одного уравнения по второму закону Кирхгофа. Схема замещения показана на рис. 3.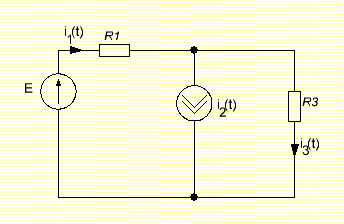



Рис. 3. Схема замещения цепи в момент после коммутации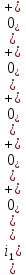



i₁(0₊) из первого уравнения системы подставим во второе уравнение. Получим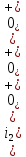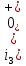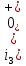







Тогда, из первого уравнения исходной системы найдем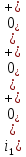



Напряжение на индуктивности в момент после коммутации: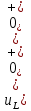



После окончания переходного процесса в цепи протекают постоянные токи, соответственно, индуктивность можно представить как короткозамкнутый участок (рис. 4).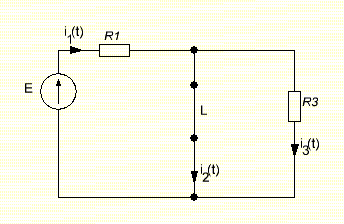



Рис. 4. Схема замещения цепи после окончания переходного процесса

Так как резистор R₂ после коммутации замкнут накоротко ключом, то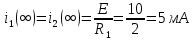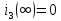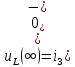







2. Рассчитаем токи классическим методом. Так как цепь содержит один реактивный элемент (индуктивность), то ток через индуктивность i₂(t) будем находить в виде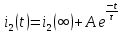



где A – постоянная интегрирования;

τ – постоянная времени цепи.

Постоянную интегрирования, запишем выражение для тока при t=0.



Откуда



Постоянная времени цепи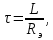



где R_э – эквивалентное сопротивление цепи относительно катушки индуктивности в режиме после коммутации (рис. 5).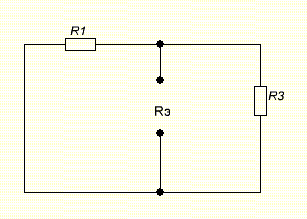



Рис. 5. Схема замещения для определения эквивалентного сопротивления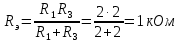



тогда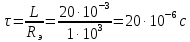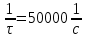





Выражение для тока примет вид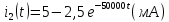



Определим напряжение на индуктивности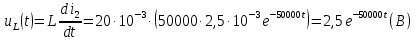



Токи в ветвях: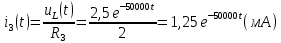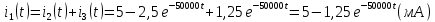





Выполним проверку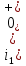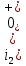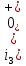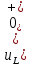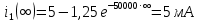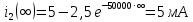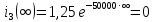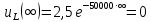

















Результат соответствует расчету, полученному в предыдущем пункте.

3. Построим графики токов и напряжения на индуктивности в функции времени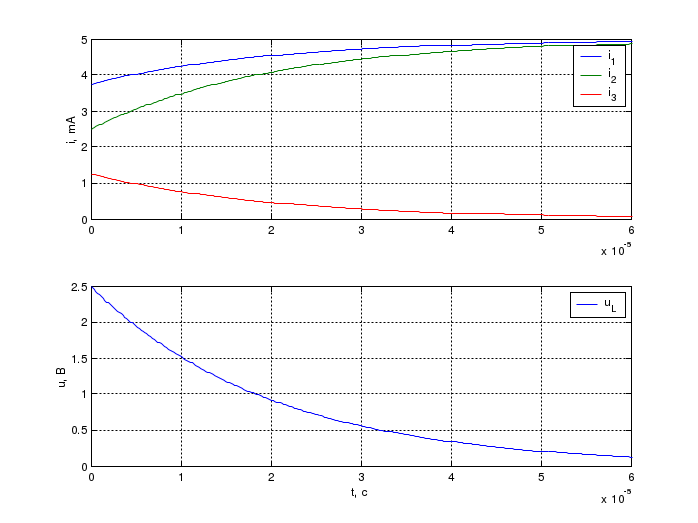



Рис. 6. Графики токов в ветвях и напряжения на индуктивности

Как видим, переходный процесс завершается с 5% точностью за время 3τ=60 мкс.

4. Рассчитаем ток i₂(t) операторным методом. Для расчета воспользуемся схемой замещения послекоммутационной цепи в операторном виде (рис. 7).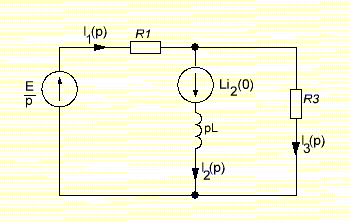



Рис. 7. Операторная схема замещения цепи

Для расчета тока I₂(p) удобно воспользоваться методом эквивалентного генератора. Представим цепь в виде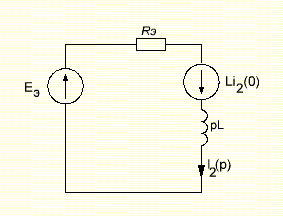



Рис. 8. Операторная эквивалентная схема замещения цепи

Найдем параметры эквивалентной схемы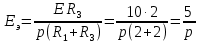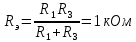





Тогда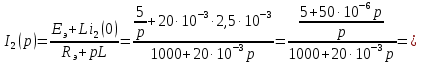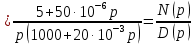





Для нахождения оригинала воспользуемся теоремой разложения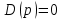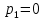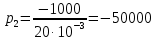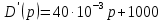









Тогда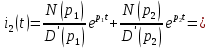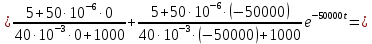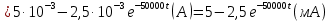







Результат совпадает с найденным классическим методом.

Задача 2

Задача посвящена временному и частотному (спектральному) методам расчета реакции цепей на сигналы произвольной формы. В качестве такого сигнала используется импульс прямоугольной формы. Электрические схемы цепей содержат емкости С или индуктивности L, а также сопротивления R. Для всех вариантов R₂=3R.

_{В схемах, где имеется сопротивление} R₃ , его величина R₃  0,2R₁ . Во всех схемах входным напряжением u₁tявляется прямоугольный импульс длительностью t_ии амплитудой U_1.

1. 
   Перерисуйте схему Вашего варианта (см. табл. 1 и табл. 5). Выпишите исходные данные Вашего варианта (таблица4).
   

Временной метод расчета

2. 
   Рассчитайте переходную g₂(t) и импульсную h₂(t) характеристики цепи по напряжению классическим или операторным методами (по выбору).
   
3. 
   Рассчитайте реакцию цепи в виде выходного напряжения, используя:
   

- интеграл Дюамеля;

- интеграл наложения

4. Постройте временные диаграммы входного и выходного напряжений в одинаковом масштабе

Частотный метод расчета

5. Рассчитайте комплексные спектральные плотности входного U₁(jω) и выходного U₂(jω) сигналов.

6. Запишите выражение комплексной передаточной функции цепи .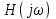

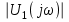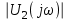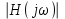7. Рассчитайте и постройте графики модулей , и модуля комплексной передаточной функции цепи , как функции от частоты ω в диапазоне частот 0 – 3/t_и.

Исходные данные (вариант 1)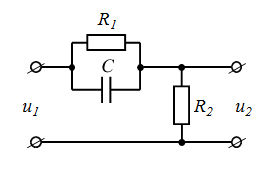



Рис. 1. Схема цепи (2)

C=20 пФ; R₁=1 кОм; R₂=3 кОм; t_и=30 нс; U₁=3 В

Решение

1. 
   Рассчитаем переходную характеристику цепи. Пусть на вход цепи подается напряжение 1 В. Тогда, в установившемся режиме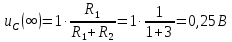
   

Постоянную времени цепи определим из соотношения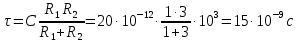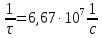





Напряжение на емкости будет определяться выражением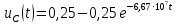



Ток через емкость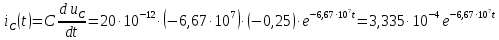



Ток через сопротивление R₁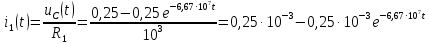



Ток через R₂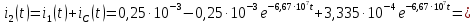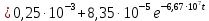





Тогда, напряжение на выходе будет представлять собой переходную характеристику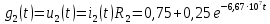



Импульсную характеристику получим, продифференцировав выражение для переходной характеристики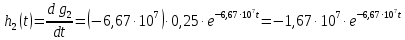

2. 
   Для расчета реакции цепи запишем интеграл Дюамеля. Так как входное напряжение в момент времени t_и испытывает разрыв, то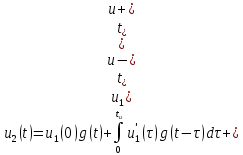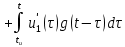
   

Поскольку 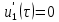(функция кусочно-постоянная), то выражение для реакции цепи примет вид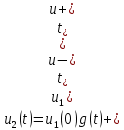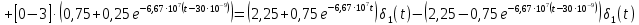





Запишем интеграл наложения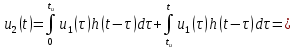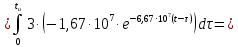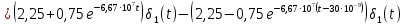







Построим графики входного воздействия и реакции цепи (рис. 2).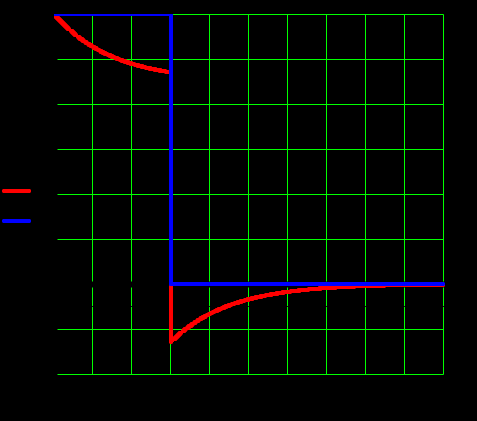



Рис. 2. Временные диаграммы входного сигнала и реакции цепи

3. 
   Запишем спектральные плотности входного и выходного сигналов. Для записи спектральной плотности входного сигнала представим его в виде разности двух ступенчатых сигналов.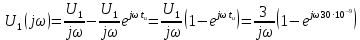
   

Модуль спектральной плотности входного сигнала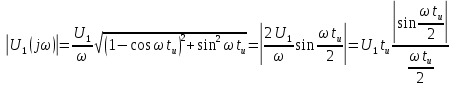

4. 
   Комплексная передаточная функция цепи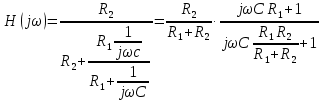
   

Найдем модуль комплексной передаточной функции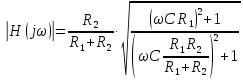



Тогда, спектральная плотность выходного сигнала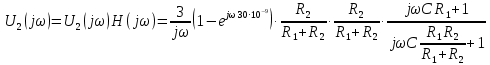



Модуль спектральной плотности: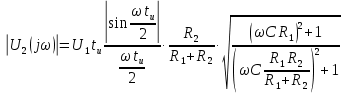

5. 
   Построим графики спектральной плотности входного и выходного сигнала и модуль передаточной функции цепи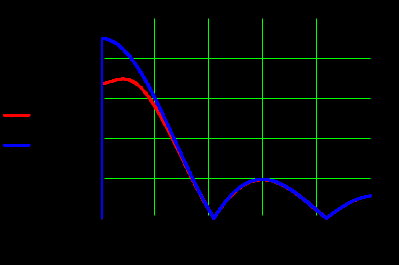
   

Рис. 3. Зависимость спектральной плотности входного и выходного сигнала от частоты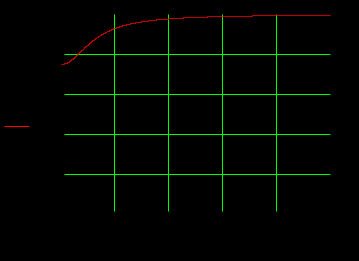



Рис. 4. Зависимость модуля передаточной функции цепи от частоты