математическое моделирование. Задание 2 ЭОС. Задача При проверке прочности бетонных кубиковобразцов были получены следующие результаты, мпа 200 220 250 210 230

• Название: Задача При проверке прочности бетонных кубиковобразцов были получены следующие результаты, мпа 200 220 250 210 230
• Анкор: математическое моделирование
• Дата: 13.12.2021
• Размер: 19.27 Kb.
• Имя файла: Задание 2 ЭОС.docx
• Тип: Задача; #301806

Задание 2.

Решаем из пособия «Планирование эксперимента» задачи 5-9.

Задача 5.

При проверке прочности бетонных кубиков-образцов были получены следующие результаты, МПа:

200; 220; 250; 210; 230.

Найти несмещенные оценки для математического ожидания и дисперсии,

указать число степеней свободы оценки дисперсии.
Решение

Таблица для расчета показателей.

x	(x-xср)2
200	484
210	144
220	4
230	64
250	784
1110	1480

Для оценки ряда распределения найдем следующие показатели:

Математическое ожидание

= 1110/5 = 222

Несмещенная оценка дисперсии - состоятельная оценка дисперсии (исправленная дисперсия).

= 1480/4 = 370

Число степеней свободы выборочной дисперсии ƒ = 5 – 1 = 4.

Задача 6.

По выборке задачи 2 найти несмещенные оценки для математического ожидания и дисперсии, указать число степеней свободы оценки дисперсии.

Решение

Таблица для расчета показателей.

Группы	Середина интервала, xцентр	Кол-во, fi	xi·fi	(x-xср)2·fi
5 - 10	7,5	4	30	998,56
10 - 15	12,5	6	75	699,84
15 - 20	17,5	16	280	538,24
20 - 25	22,5	36	810	23,04
25 - 30	27,5	24	660	423,36
30 - 35	32,5	10	325	846,4
35 - 40	37,5	4	150	806,56
Итого		100	2330	4336

Математическое ожидание
Несмещенная оценка дисперсии

=

Число степеней свободы несмещенной оценки дисперсии n = 100 - 1= 99

Задача 7.

По выборке задачи 3 найти несмещенные оценки для математического ожидания и дисперсии, указать число степеней свободы оценки дисперсии.

М50	2
М75	1
М50	2
М75	3
М50	3
М50	2
М75	1
M100	2
M150	2
M75	2

Построим расчетную таблицу

xi	fi	xi*fi	(xi-xcp)^2*fi
50	9	450	5076,56
75	7	525	10,94
100	2	200	1378,13
150	2	300	11628,13
Сумма	20	1475	18093,75

Математическое ожидание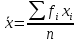

= 1475/20 = 73,75

Несмещенная оценка дисперсии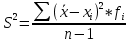

= 18093,75/19 = 952,30

Число степеней свободы выборочной дисперсии n = 20 – 1 = 19.

Задача 8.

По выборке задачи 4 найти несмещенные оценки для математического ожидания и дисперсии, указать число степеней свободы оценки дисперсии.

Таблица для расчета показателей.

Группы	Середина интервала, xцентр	Кол-во, fi	xi·fi	(x-xср)2·fi
11 - 13	12	8	96	130.573
13 - 15	14	42	588	174.787
15 - 17	16	51	816	0.0816
17 - 19	18	37	666	142.139
19 - 21	20	12	240	188.179
Итого		150	2406	635.76

Математическое ожидание
Несмещенная оценка дисперсии

= 4,27

Число степеней свободы выборочной дисперсии n = 150 – 1 = 149.

Задача 9.

Ниже дана выборка для прочности на разрыв. Определить среднее значение и дисперсию выборки

R H/м^2	Частота
18461	2
18466	12
18471	15
18476	10

Таблица для расчета показателей.

xi	Кол-во, fi	xi·fi	(x-xср)2·fi
18461	2	36922	170.414
18466	12	221592	214.793
18471	15	277065	8.876
18476	10	184760	332.84
Итого	39	720339	726.923

Математическое ожидание
Несмещенная оценка дисперсии

=