Однородность двух групп означает. Задача про йогрут

Название	Задача про йогрут
Дата	02.05.2019
Размер	45.15 Kb.
Формат файла
Имя файла	Однородность двух групп означает.docx
Тип	Задача #75914

Задача про йогрут

Однородность двух групп означает, что соответствующие им вероятности равны, неоднородность - что эти вероятности отличаются. В терминах математической статистики: необходимо проверить гипотезу однородности

H₀:p₁=p₂

при альтернативной гипотезе

H₁:p₁

p₂.

. Вычислить статистику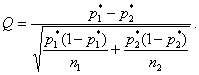

Выбор в городе А – 120/660 = 0,182

Выбор в городе Б – 70/350 = 0,200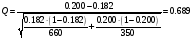

2. Сравнить значение модуля статистика |Q| с граничным значением K. Если |Q|<K, то принять гипотезу однородности H₀ . Если же |Q|>K, то заявить об отсутствии однородности и принять альтернативную гипотезу H₁ .

Ф(К)= (1-)/2 = (1-0,1)/2 = 0,45

K = 1.65 > Q то принимаем гипотезу однородности H₀

Т.е. популярность йогурта на уровне значимости 10% одинакова

При

Ф(Q)= Ф(0,689)= 0,255

(1-)/2 = 0,255

1 -  = 0.510

 = 0,490 = 49%

При значимости 49%.

Нулевая гипотеза $h_0:\; \bar x = \mu$ (выборочное среднее равно заданному числу $\mu$ ).

Статистика критерия: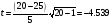

$\displaystyle t = \frac{(\bar x - \mu)\sqrt{m}}{s}$

имеет распределение Стьюдента с

степенями свободы, где

Критерий (при уровне значимости $\alpha$ ):

против альтернативы $h_1:\; \bar x \neq \mu$

если $|t|> t_{\alpha/2}$ , то нулевая гипотеза отвергается;

t_0.05 = 2.0930

4.539 >2.0930, гипотеза о неизменности расхода отвергается.

против альтернативы $h\'_1:\; \bar x < \mu$ - если $t < t_{\alpha}$ , то нулевая гипотеза отвергается;

-4.539 < 1.7291, расход уменьшился.

На практике нулевая гипотеза Н₀: E(S²) =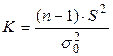

проверяется, если нужно проверить точность приборов, методики контроля ритмичности работы и т.д. В качестве критерия проверки нулевой гипотезы примем случайную величину

K = (20-1)*5*5/(3*3) = 52,78.

Здесь S² - выборочная исправленная дисперсия. Можно показать, что случайная величина К имеет теоретическое распределение

с (n - 1)-й степенью свободы.

Критерий Хи квадрат (19) с уровнем значимости 0,1 = 11.65091 ,

Т.е. разброс значений увеличился значимо.
Таблица для расчета показателей.

x_i	Кол-во, f_i	x_i * f_i	Накопленная частота, S	\|x - x_ср\|*f	(x - x_ср)²*f	Частота, f_i/n
0	10	0	10	20.11	40.46	0.0575
1	26	26	36	26.3	26.6	0.15
2	96	192	132	1.1	0.0127	0.55
3	40	120	172	39.54	39.09	0.23
4	0	0	172	0	0	0
5	0	0	172	0	0	0
6	2	12	174	7.98	31.82	0.0115
Итого	174	350		95.03	137.98	1

2. Проверим гипотезу о том, что Х распределено по закону Пуассона.

где p_i — вероятность попадания в i-й интервал случайной величины, распределенной по гипотетическому закону.
а) Находим по заданному эмпирическому распределению выборочную среднюю (x_В = 2.011).
б) Принимаем в качестве оценки параметра λ распределения Пуассона выборочную среднюю x_ср = 2 Следовательно, предполагаемый закон Пуассона имеет вид:

Pi = 2ⁱ/i!*e^-2
в) Найдем по формуле Пуассона вероятности P_i, появления ровно i событий в n испытаниях. Находим теоретические частоты по формуле np_i
i = 0: p₀ = 0.13, np₀ = 23.28
i = 1: p₁ = 0.27, np₁ = 46.83
i = 2: p₂ = 0.27, np₂ = 47.1
i = 3: p₃ = 0.18, np₃ = 31.58
i = 4: p₄ = 0.0913, np₄ = 15.88
i = 5: p₅ = 0.0367, np₅ = 6.39
i = 6: p₆ = 0.0123, np₆ = 2.14
Объединим малочисленные частоты: (6,5,4,3) и соответствующие им теоретические частоты.
в) Вычисляем слагаемые статистики Пирсона по формуле (5 столбец таблицы):

i	Наблюдаемая частота n_i	p_i	Ожидаемая частота np_i	Слагаемые статистики Пирсона K_i
0	10	0.13	23.28	7.57
1	26	0.27	46.83	9.26
2	96	0.27	47.1	50.78
3	42	0.32	55.99	3.49
	174			71.12

Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение _набл, тем сильнее довод против основной гипотезы.
Поэтому критическая область для этой статистики всегда правосторонняя: [_kp;+∞).
Её границу _kp = χ²(k-r-1;α) находим по таблицам распределения γ² и заданным значениям s, k (число интервалов), r=1 (параметр λ).
kp(0.01;2) = 9.21034; Kнабл = 71.12
Наблюдаемое значение статистики Пирсона попадает в критическую область: Кнабл > Kkp, поэтому есть основания отвергать основную гипотезу. Данные выборки распределены не по закону Пуассона.

ad = 32 28 896

bc= 25 40 1000

Р = (25+28) / (32+25+40+28) = 0,424

	Автомоб	Грузов
Резина А	33	39
Резина Б	57*0,424=24	68*0,424=29
	57	68

Критерий хи квадрат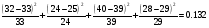

<6.635, т.е. различия между износами не значимы.