Главная страница
Навигация по странице:

  • Федеральное государственное бюджетное образовательное учреждение высшего образования «Московский государственный технический университет

  • Решение

  • Задача 2. Прибор состоит из трех блоков , интенсивности отказов которых соответственно равны: λ

  • Задача 3 . Из партии объемом N = 1000 изделий взята выборка n =100 экземпляров. Установлены приемочное и браковочные числа: A

  • = 0,2 с использованием формул гипергеометрического и f-биномиального распределений.

    		•

    Домашнее задание по надежности ракетного и ствольного оружия. ДЗ по надежности РиСО. Задача Проектируется нерезервированная система, состоящая из элементов четырех групп. Количество элементов каждой группы, а также интенсивности их отказов приведены в таблице


    Скачать 49.97 Kb.
    НазваниеЗадача Проектируется нерезервированная система, состоящая из элементов четырех групп. Количество элементов каждой группы, а также интенсивности их отказов приведены в таблице
    АнкорДомашнее задание по надежности ракетного и ствольного оружия
    Дата08.12.2021
    Размер49.97 Kb.
    Формат файлаdocx
    Имя файлаДЗ по надежности РиСО.docx
    ТипДокументы
    #295973
    Министерство образования и науки Российской Федерации

    Федеральное государственное бюджетное образовательное учреждение

    высшего образования

    «Московский государственный технический университет

    имени Н.Э. Баумана

    (национальный исследовательский университет)»

    (МГТУ им. Н.Э. Баумана)



    ФАКУЛЬТЕТ «СПЕЦИАЛЬНОЕ МАШИНОСТРОЕНИЕ»
    КАФЕДРА СМ6 «РАКЕТНЫЕ И ИМПУЛЬСНЫЕ СИСТЕМЫ»


    Домашнее задание

    по курсу «Надёжность РиСО»

    Студент:
    Группа:
    Преподаватель:


    Москва, 2021 г.

    Вариант 9.

    Задача 1. Проектируется нерезервированная система, состоящая из элементов четырех групп. Количество элементов каждой группы, а также интенсивности их отказов приведены в таблице.

    Номер группы
    Число элементов
    Интенсивность отказа элемента, час-1

    1
    10
    2∙10-6

    2
    15
    4∙10-6

    3
    32
    2,5∙10-6

    4
    8
    5∙10-6

    Определить следующие показатели надежности детали:

    – интенсивность отказов системы;

    – среднее время безотказной работы;

    – вероятность безотказной работы системы в течение времени t1=100 ч, t2=1000 ч и в интервале указанных наработок;

    – плотность распределения времени безотказной работы системы при наработке t2=1000 ч.

    Решение:

    Интенсивность отказа: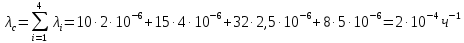



    Среднее время безотказной работы: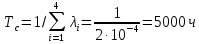



    Вероятность безотказной работы системы в течение времени 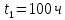, 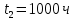и в интервале указанных наработок:







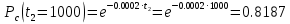    Плотность распределения времени безотказной работы системы при наработке :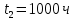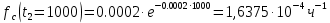


    Задача 2. Прибор состоит из трех блоков, интенсивности отказов которых соответственно равны: λ1=4⋅10−4 1/ч, λ2 = 2,5⋅10−4 1/ч, λ3 =3⋅10−3 1/ч. Требуется рассчитать вероятность безотказной работы прибора при t=100 ч для следующих случаев: а) резерв отсутствует; б) имеет место общее дублирование прибора в целом.

    Pi = e-λit

    P1 = e-4‧10^-4‧100=0,961

    P2 = e-2,5‧10^-4‧100=0,975

    P1 = e-3‧10^-3‧100=0,97

    Случай а): Р(100)=Р1‧Р2‧Р3=0,909

    Случай б), примем m=2:

    P(t) = 1 – (1 – nNi=1Pi(t))m

    P(100) = 1 – (1 – Р1‧Р2‧Р3)2 = 0,992
    Задача 3. Из партии объемом N = 1000 изделий взята выборка n =100 экземпляров. Установлены приемочное и браковочные числа: A0=3, A1=4. Определить риск поставщика и риск заказчика, если q0 = 0,02, а q1 = 0,2 с использованием формул гипергеометрического и f-биномиального распределений.

    D0=q0‧N=0,02‧1000=20

    D1=q1‧N=0,2‧1000=200

    Воспользуемся формулами гипергеометрического распределения: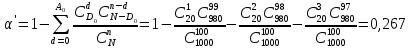





    Воспользуемся формулами f-биномиального распределения:

    f = n/N=100/1000=0,1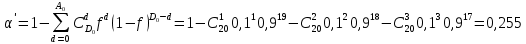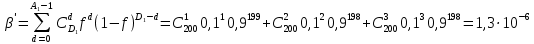

    написать администратору сайта